准三能级固体激光器中激光介质长度优化*

王垚廷,时文嘉,张艳超

(西安工业大学 理学院,西安 710021)

依照激光原理可知,相同激活粒子的激光介质中准三能级激光系统实现的受激辐射波长较四能级激光系统短。以掺钕(Nd)激光介质为例,其准三能级受激辐射波长在900 nm波段,而四能级系统在1 060 nm波段。900 nm波段的激光器可以应用于水蒸气探测,测量臭氧差分吸收激光雷达,掺镱激光介质泵浦源以及通过倍频得到蓝光激光器等方面。文献[1]研究结果表明,激光二极管端面泵浦掺Nd激光介质实现的准三能级全固态激光器是目前获得900 nm波段激光器的最有效方法。Nd:GdVO4晶体作为一种比较新型的激光介质,相对目前较成熟的掺Nd激光介质Nd:YAG和Nd:YVO4,其在泵浦吸收效率及热导率方面有着明显优势[2-3]。另外,Nd:GdVO4激光晶体在900 nm波段的受激辐射截面为6.6×10-20cm2,明显高于Nd:YAG (4.8×10-20cm2)和Nd:YVO4(3.7×10-20cm2)[3]。因此,Nd:GdVO4激光晶体是实现900 nm波段受激辐射的理想选择。

很多国内外学者开展了关于激光二极管端面泵浦准三能级激光器的研究。早在1987年,斯坦福大学的研究人员就以Nd:YAG为例给出了准三能级激光器运转的速率方程[4]。文献[5]将能量传输上转化效应引入准三能级激光系统的速率方程,并得到实验验证。能量传输上转换效应是指处于激光上能级的任意两个粒子,其中一个向较低能级跃迁,同时释放能量；另一个粒子吸收该能量,从而跃迁到较高能级,然后两个粒子快速地以无辐射跃迁的形式分别到达基态和激光上能级。从高能级向低能级无辐射跃迁的过程会将两能级之间的相对能量全部转化为热量[6-7]。文献[8]认为,激发态吸收是掺Nd激光器中不可忽略的一种效应。激发态吸收是指处于亚稳态的粒子,通过吸收泵浦光子或受激辐射光子而跃迁到更高能级,然后以自发辐射或无辐射跃迁的形式到达较低能级或者基态。能量传输上转换效应和激发态吸收效应会直接导致激光上能级粒子数减少,从而降低激光转化效率,同时产生热量,加剧激光介质的热效应[9-10]。文献[11]将能量传输上转化效应和激发态吸收效应同时引入激光二极管端面泵浦的Nd:GdVO4准三能级激光系统的速率方程,并进行了初步研究。在此基础之上,文献[12]详细分析了激光二极管端面泵浦Nd:GdVO4激光器的热沉积百分比,并给出相应的理论模式,得到理论结果和实验结果相符合。但是,准三能级激光器的一些固有缺点仍然限制其转化效率的提高[13-14],一方面,准三能级激光系统中的激光下能级必然存在一定数量的粒子,导致自吸收损耗；另一方面,受激辐射截面相对四能级激光系统很低,两方面原因同时导致低的转换效率和严重的热效应。文献[13-14]提出了一些提高准三能级激光器转化效率的方法,包括降低泵浦光斑尺寸,采用复合激光介质,直接泵浦到激光上能级,以及优化谐振腔以补偿热效应等。其中,降低泵浦光斑尺寸可以降低阈值和自吸收损耗,但会导致热效应严重；采用复合介质和直接泵浦到激光上能级可以减弱激光介质热效应；优化谐振腔是针对严重的热效应增加谐振腔的稳区范围,以增加泵浦功率。但端面泵浦固体激光器的准三能级速率方程仍可继续优化,并以此为基础对激光介质长度进行优化。

本文采用能量传输上转化效应和激发态吸收效应的准三能级激光系统速率方程,分析推导出自吸收损耗的解析表达式,并理论计算输出功率和激光介质长度的关系,将该理论应用到激光二极管端面泵浦的Nd:GdVO4912 nm激光器中,理论结果和实验结果相符合。

1 理论推导

为更详细地模拟准三能级激光系统的运转模式,在已有的速率方程中引入能量传输上转换效应和激发态吸收效应。由于在激发态吸收过程中,无论是吸收泵浦光子还是吸收受激辐射光子,其结果均为降低激光转化效率,因此两个过程可以用一个等效的吸收截面参数σESA来表示。以激光二极管端面泵浦的掺Nd准三能级激光器为例,其稳态时的准三能级系统粒子数反转密度ΔN(r,z)和激光谐振腔内受激辐射光子总数Φ的速率方程[7-8]可以分别表示为

(1)

(2)

式中：r,z和t分别为径向、轴向和时间变量；τ为自发辐射时间常数；c为真空中光速；σem为受激辐射界面；σESA为等效激发态吸收截面；n为激光介质对应的受激辐射波长折射率；ΔN0为初始时刻(未泵浦)粒子数反转密度；ΔN′(r,z)为相应的四能级系统的粒子数反转密度；W为能量传输上转换参数；f=fa+fb,fa和fb分别为激光下能级占据基态粒子数百分比和激光上能级占据亚稳态粒子数百分比；R为泵浦速率；τc为腔内受激辐射光子时间常数；rp(r,z)和φ0(r,z)分别为泵浦光束和谐振腔内振荡激光场空间分布函数。

针对本文实验装置,泵浦光束空间分布函数rp(r,z)为

(3)

式中：α为激光介质对泵浦光的吸收系数；L为激光介质长度；ωpa为激光介质内泵浦光斑半径平均值。谐振腔内振荡激光场空间分布函数φ0(r,z)为

(4)

式中：Lc为激光介质光程；ω0为激光介质内振荡激光光斑半径。泵浦速率R和谐振腔内受激辐射光子总数Φ可表示为

(5)

式中：Pp为泵浦功率；ηa为激光介质对泵浦光的吸收效率；Pout为激光器输出功率；T为激光谐振腔输出耦合透射率；hυp和hυl分别为泵浦光子和受激辐射光子能量。

通过方程式(1)解得粒子数反转密度ΔN(r,z)并代入方程式(2),再结合式(3)～(5)以及相关实验参数,通过数值计算可以获得输出功率Pout、泵浦功率Pp、输出耦合透射率T以及激光介质长度L等关键参数之间的关系。

谐振腔内光子数速率方程式(2)的等式右边,如果忽略掉第二项,剩余部分则和四能级系统的粒子数反转密度速率方程完全相同。准三能级激光系统和四能级激光系统的本质区别在于准三能级系统中激光下能级存在一定数量的粒子。因此,该项可以解释为由于准三能级系统中激光下能级粒子数不为零造成的自吸收损耗δrea,表达示为

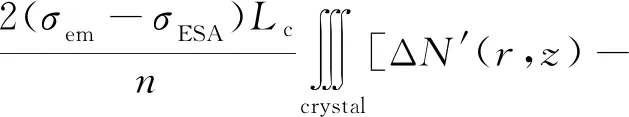
ΔN(r,z)]φ0dV。

(6)

式(6)中的ΔN′(r,z)和ΔN(r,z)可以通过求解速率方程式(1)和方程式(2)得到。将本文的实验参数代入式(6),可以理论计算得到不同泵浦功率条件下自吸收损耗δrea和激光介质长度L之间的关系,计算结果如图1所示。由图1可以看出,自吸收损耗和介质长度之间呈增函数关系,即自吸收损耗随激光介质长度增加而增加。根据激光原理可知,激光产生过程中,其增益必然随着介质长度呈增加关系。因此,损耗和增益共同作用会导致存在最佳介质长度,使得激光输出功率最大化。从图1还可以看出,自吸收损耗和泵浦功率呈减函数关系,即随着泵浦功率的增加,自吸收损耗降低。

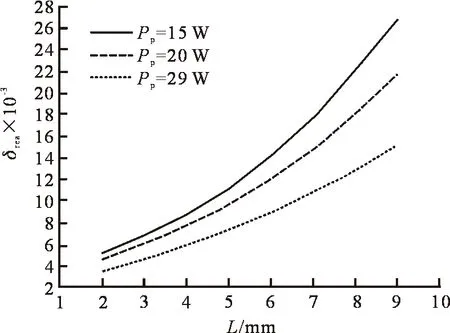
图1 自吸收损耗δrea和激光介质长度L关系图

2 实验设计

为验证上文所提到的最佳激光介质长度的存在,实验设计了激光二极管端面泵浦的Nd:GdVO4912 nm激光器示意图,如图2所示。泵浦源为光纤耦合的808 nm激光二极管(Laser Diode,LD),其芯径和数值孔径分别为300 μm和0.08。光纤耦合输出的泵浦光经透镜按照1∶1的成像比例聚焦到激光介质Nd:GdVO4中。激光介质为双端复合结构,即两端不掺杂,中间掺杂,且两端不掺杂部分均为3 mm,中间掺杂部分长度将在本实验中优化。介质横截面为2.5 mm×2.5 mm,该尺寸小于常用的激光介质尺寸(3 mm×3 mm),其目的在于降低激光介质本身温度和温度梯度,从而减小自吸收损耗和减弱热效应。介质两端面镀膜参数为：912 nm减反(R912 nm<0.2%)、808 nm高透(T808 nm> 99%)和1 064 nm高透(T1 064 nm>95%)。实验过程中,整个激光介质侧面用高热导率的金属铟包裹,并置放于热导率更高的紫铜夹具中,因为介质侧面磨砂,从而可保证良好的散热效果。紫铜夹具被精密控温,且控温精度为0.1 ℃,实验中激光介质和夹具整套装置温度被控制在20 ℃。激光谐振腔由平面镜M1和平凹镜M2组成,其中M1为输入镜,镀膜参数为912 nm高减反(R912 nm>0.2%)、808 nm高透(T808 nm>99%)和1 064 nm高透(T1 064 nm>95%)；M2为输出耦合透视镜,镀膜参数为T912 nm= 3%。实验中可以通过调节M1和M2之间的距离来调整激光介质中振荡光斑的半径值w0,从而保证激光介质中振荡光斑和泵浦光斑的最佳交叠。

图2 实验装置示意图

3 结果及分析

为优化激光介质长度以获得最大912 nm激光输出功率,实验上选取了5种不同长度(掺杂部分)的Nd:GdVO4激光晶体,分别为L=3 mm、L=4 mm、L=5 mm、L=6 mm和L=7 mm。实验测量的输出功率Pout和泵浦功率Pp之间的关系如图3所示。由图3可以看出,长度为3 mm的介质输出功率明显低于其他长度,这是由于介质太短,导致对泵浦光吸收效率太低。另外,可以明显看出长度为5 mm、6 mm和7 mm的3种晶体在较大泵浦功率时输出功率增加明显,这是因为随着泵浦功率的增加,腔内光子数会增多,导致自吸收损耗会逐渐降低,而此时较长的激光介质会吸收更多的泵浦能量,从而输出功率会明显增加。此外,激光晶体长度在3～7 mm范围内,阈值泵浦功率随晶体长度增加而增加,原因在于该长度范围内阈值处的自吸收损耗大于泵浦吸收。根据前文所述,准三能级激光器运转过程中自吸收损耗会随着泵浦功率增加而降低,随着晶体长度的增加会出现泵浦吸收饱和,导致自吸收损耗占据优势,从而表现出斜效率随着晶体长度变长先增加后降低的现象,因此实验数据曲线会出现交叉现象,即不同泵浦功率条件下的最大输出功率对应的激光介质长度并不相同,进而表现出基于最大输出功率的最佳晶体长度。

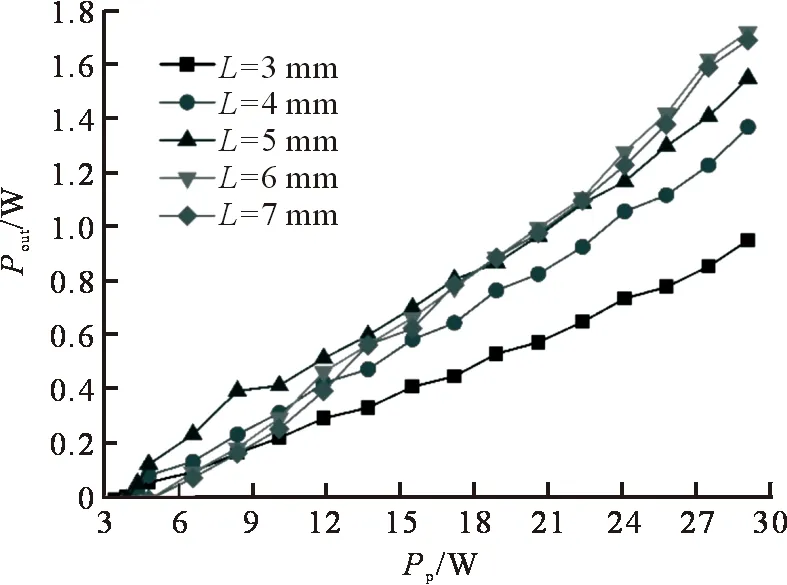
图3 实验测量的输出功率Pout和泵浦功率Pp关系图

根据速率方程式(1)和式(2)可以理论计算出泵浦功率Pp分别为15 W和29 W时,输出功率Pout和激光介质长度L之间的关系,如图4～5所示,其中,实线为同时包括能量传输上转换(ETU)和激发态吸收效应(ESA)的理论计算结果,虚线为同时忽略能量传输上转换效应(ETU)和激发态吸收效应(ESA)的理论计算结果；方点为从图2中得到的实验数据。

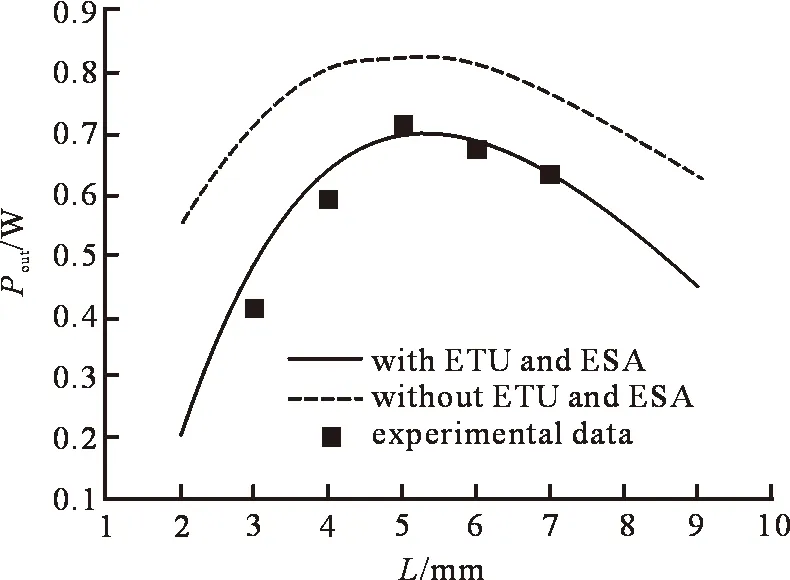
图4 输出功率Pout和激光介质长度L关系图(Pp=15 W)

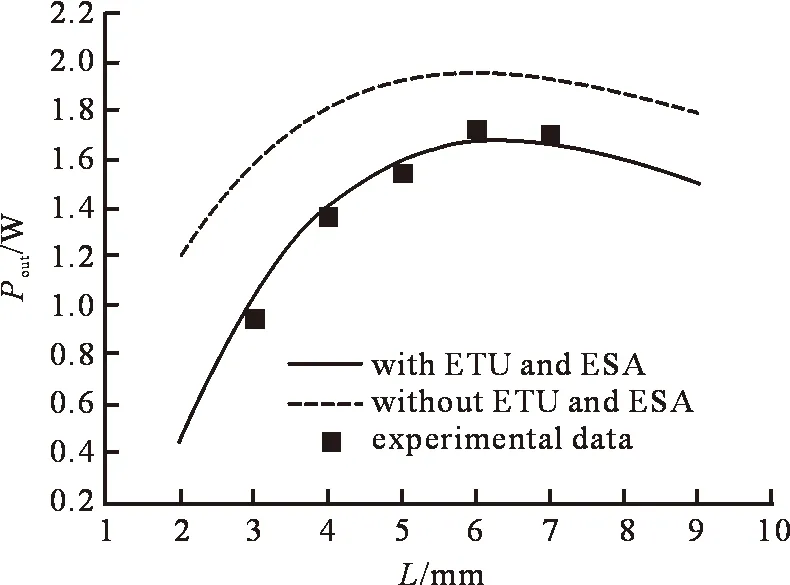
图5 输出功率Pout和激光介质长度L关系图(Pp=29 W)

由图4和图5分别可以看出,理论计算的最佳激光介质长度分别为5.2 mm和6.4 mm,且实验结果与包括能量传输上转换效应和激发态吸收效应的理论结果更相符,证明本文理论分析的正确性。速率方程式(1)和方程式(2)计算结果表明：泵浦功率在5～30 W范围内,理论结果和实验结果均能较好贴合,最佳激光介质均在5～6.5 mm之间,且呈递增关系,而本实验中泵浦源最大输出功率为30 W。为保证理论计算的科学性,同时尽可能还原激光器实际运转状态,应满足以下条件：① 除泵浦功率Pp外,其他所有参数在整个计算过程中必须保持不变；② 必须考虑随着泵浦功率增加导致的热效应变化以及热效应对激光谐振腔的影响,从而确保理论计算结果能够更加如实的反映激光器实际状况[15]。

4 结 论

1) 将能量传输上转换效应和激发态吸收效应引入准三能级速率方程,分析推导了自吸收损耗的解析表达式。理论计算表明,自吸收损耗同激光介质长度和泵浦功率分别呈增函数和减函数关系。

2) 理论计算表明,最佳激光介质长度随着泵浦功率递增,且在5 ～6.5 mm之间(泵浦功率在30 W以内)。理论结果可以得到实验验证。