分布式存储中一种新的低修复带宽的Hitchhiker码
2020-07-13胡金平李贵洋江小玉韩鸿宇
胡金平,李贵洋,江小玉,周 悦,韩鸿宇
(四川师范大学 计算机科学学院,成都 610101)
1 前 言
海量数据的增加导致存储系统应具有低价格和可扩展的优良特性.相比传统的集中式存储[1],分布式存储系统[2]利用廉价的商用PC机和成熟的网络技术,形成了成本低廉且易扩展的存储系统.为保证数据的可靠性,分布式存储系统常利用多副本[3]和纠删码[4,5]这两种容错技术.前者较成熟且最简单,但空间利用率低;后者以其高容错能力,高空间利用率等优点得到学术界和工业界的关注,并广泛应用到Hadoop[6]、GFS[7]、Azure[8]等各大分布式存储系统中.
Reed-Solomon Codes[9,10]是具有MDS[11]性质的纠删码,能够达到理论上的最高容错能力和最低的存储代价,但存在修复成本高昂的问题.为了降低修复带宽,目前常用的有两种降低修复带宽的方式.一是Rashmi等人[12]提出了Piggybacking设计架构,其中将易于工程实现的双条带MDS码命名为Hitchhiker[13]码,并给出了三种Hitchhiker码的构造方案,适用于各种(k,r)参数配置.二是Gopalan 等人[14-16]分别提出了局部修复性编码(Locally Repairable Codes),简称LRC.它通过添加局部校验来减少磁盘I/O,从而降低修复成本.目前RS码、LRC和Hitchhiker码都广泛应用于各大分布式存储系统中.例如:RS(6,3),RS(8,4),RS(10,4)分别应用到了Google文件系统[17]、Baidu Atlas云平台[18]和Facebook存储系统[19]中,在Hadoop分布式文件系统提供多种参数的RS(k,r)码[20]供用户选择;LRC应用在Azure和Hadoop中[21,22],两者的编码方式有稍许差异;(10,4)-Hitchhiker已部署在Hadoop文件系统中.
目前Hitchhiker码只针对系统单元的修复进行了优化,而对校验单元未做处理.LRC虽能显著的降低单节点失效的修复带宽,但由于增加了额外的存储开销,从而破坏了MDS性质.针对该问题,本文借鉴LRC中的信息位局部性的思想,构造出两种Hitchhiker码与LRC相结合的新编码,并命名为——Hitchhiker-LRC和Hitchhiker-LRC+.它们既没有增加额外的存储空间又降低数据单元和校验单元的修复带宽,达到整体修复带宽优于原Hitchhiker码.本文首先给出了将LRC码加入到Hitchhiker码的校验单元中的理论基础.其次,提出了Hitchhiker-LRC和Hitchhiker-LRC+的主要思想和编解码方法.然后,对新提出的编码的修复带宽率、编码时间和解码时间进行了理论的分析,并讨论了参与局部校验的数量l与修复带宽率关系.最后,实验证明了在2≤r 首先参数列表,如表1所示. 表1 参数表 Table 1 Parameter list 参数意 义n单元总数k存放原始数据单元的个数r校验单元数量l参与局部校验的数量pk与r-1的商,每个校验中附加的数据的个数qk与r-1的余数,每个校验附加后剩下的数据的个数δ修复每个单元所需的帮助数量之和δ-修复每个单元所需的平均下载量γ修复失效单元的平均下载量占原数据总量的百分比 其次给出相关性质与定义. 性质1.将原始数据分为等大小的k份,进行编码产生r(r=n-k)个校验,将数据扩大到n份并存储到不同的n个节点上.任何k份数据都能恢复全部的n个节点中的数据.称这种性质为MDS性质. 定义1(单元).单元即units,代表某个节点中在同一个编码区域中的数据. 定义2(条带).条带即stripe,代表同一组编码的n个units的集合,n个units由k个原始数据单元和r个校验数据单元组成.子条带为一个条带分为多个子条带,用substripe表示. 局部修复编码(LRC)是以存储资源换取带宽资源的MR[23]码,由Gopalan、Oggier、Papailiopoulos等人分别提出.C.Huang 等人提出的金字塔码[24]在Azure云中得到应用.结果显示:LRC码有效的减少了磁盘I/O开销,从而降低单节点失效的修复带宽.图1为LRC(10,6,2)的编码,称由全部数据单元产生的校验p1,p2为全局校验,由部分数据单元产生的校验lp1,2,lp2,1为局部校验.通常局部校验与全局校验有一定的数量关系.在金字塔码中,全局校验与局部校验的数量关系如公式(1)所示. px=lpx,1+lpx,2+…+lpx,y (1) 它是将全局校验拆分成y个局部校验.存储时,其中的一个局部校验不存储,达到节省存储空间的目的.那么图1中的p1=p1,1+p1,2,p2=p2,1+p2,2,其中p1,1和p2,2不存储. 图2 Hitchhiker(10,4)与RS(10,4)编码的结构 3.1.1 编码过程 Hitchhiker-LRC的编码主要分为三步:一是按照Hitchhiker-nonXOR的编码.二是利用LRC的思想对第一个子条带中的校验单元求局部校验,并将结果存放在已通过局部校验的形式捎带在第二个子条带的校验的位置之上.三是利用横向减法来存储第一步中需要捎带在第一个子条带的校验单元中的数据.现以例子叙述Hitchhiker-LRC的编码过程.如图3所示,其中l=r=4. 第1步,按照Hitchhiker-nonXOR的方式进行编码,计算p=3,q=1,如公式(2)所示. (2) 可知在unit12-14的第二个子条带中分别存储3个数据,在unit12的第一个子条带中存储1个数据.如图3(a)所示. 3.1.2 解码过程 图3 Hitchhiker-LRC(10,4)编码示意图 第1步为根据丢失单元位置,判断丢失的单元的类型.如算法1中Step 1所示. 第2步为解码数据单元或解码校验单元. 解码数据单元利用Hitchhiker-nonXOR中的捎带法则或者校验单元,其思想为:利用MDS性质恢复第二个子条带中的bx,接着用第一个子条带中的LRC和横向减法来恢复ax.需用到丢失的数据单元unitx和附加在第几个校验单元的临时变量p′,其中p′为: (3) 修复dr型的方法与原Hitchhiker相同;修复dl需先利用MDS性质恢复bx,再利用校验单元中第一个子条带中的LRC和横向减法来恢复ax.如算法1中Step 2所示. g=xmod(k-2) (4) 对ps而言,需下载捎带在该校验第二个子条带的数据,计算恢复第二个子条带的数据.第一个子条带的修复同样利用LRC的修复方式.最后,修复pa类型的第二个子条带与ps相同;不同之处在于修复第一个子条带,由于横向减法的原因,会少下载unitk+i|i∈{3,…,r}中的第一个数据.如算法1中Step 3所示. 算法1.Hitchhiker-LRC的解码算法 输入:unitx|x∈{1,…,k}、type、p、q、dr、dl、pn、ps、pa. Step 1.判断丢失单元的类型.临时变量p′. 执行公式(3); SWITCH(TRUE) CASEx∈[1,p×(r-1)]:type=dr;BREAK; CASEx∈[p×(r-1)+1,k]:type=dl;BREAK; CASEx=k+1:type=pn;BREAK; CASEx=k+2:type=ps;BREAK; CASEx∈[k+3,k+r]:type=pa;BREAK; DEFAULT:error;BREAK; Step 2.解码数据单元. 下载bi|i∈{1,…,k}{x},f1(b)得到bx; IFtype==drTHEN 下载ai|i∈{p×p′+1,…,p×p′+p}{x}、fp′+2(b)⨁f2(ai)|i∈{p×p′+1,…,p×p′+p}得到ax. ELSE IFtype==dlTHEN 下载unitk+i|i∈{1,…,r}的第一个子条带、unitk+i|i∈{3,…,r}的第二个子条带和ai|i∈{p×p′+1,…,p×p′+q}{x},得ax. END IF Step 3.解码校验单元,临时变量g. 下载bi|i∈{1,…,k}得到fxmodk(b); IFtype==pnTHEN 再下载unitk+i|i∈{1,…,r}{xmodk}的第一个子条带、unitk+i|i∈{3,…,r}的第二个子条带和ai|i∈{p×p′+1,…,p×p′+q}{x},计算得到fxmodk(a). ELSE 执行公式(4); 下载ai|i∈{g×p+1,…,g×p+p},得unitx|x∈{0,…,k}的第二个子条带.再下载unitk+i|i∈{1,…,r}{xmodk}的第一个子条带和ai|i∈{p×(r-1)+1,…,p×(r-1)+q}{x}. IFtype==psTHEN 下载unitk+i|i∈{3,…,r}的第二个子条带即可. ELSE IFtype==paTHEN 下载unitk+i|i∈{4,…,r}的第二个子条带,得fxmodk(a). END IF END IF 以(k=10,r=4,p=3,q=1)为例,描述5种单元丢失后的解码方式,如图4所示.若dr型unit8丢失,需下载帮助数据如图4(a)所示.修复dl型unit10,下载的帮助数据如图4(b)所示.修复pn型unit11,下载的帮助数据如图4(c)所示.修复ps型unit12,下载的帮助数据如图4(d)所示.若pa型的unit13丢失,下载的帮助数据如图4(e)所示. 图4 5种不同类型的解码 3.2.1 Hitchhiker-LRC+的架构 随着r的增加,参与LRC的校验增加,修复时需要的帮助单元也会增加.因此利用LRC来修复的校验单元和余下的q个数据单元都会受此影响.为了减少r增大对修复带宽率的影响,使r取值范围更广,满足目前的参数配置,提出了第二种编码Hitchhiker-LRC+.它将所有的数据捎带在第二个子条带,避免余下的q个数据受校验增加的影响,达到降低其修复带宽率的目的.它虽不能保证数据单元的最优修复,但能降低整体的修复度带宽率.其架构如图5所示. 图5 Hitchhiker-LRC+的架构 3.2.2 编码过程 编码过程包括计算校验并分配捎带数据、第一个子条带求LRC和横向减法三步.后两步的方式与Hitchhiker-LRC相同,不同之处为第一步中的数据捎带分配.其如算法2所示. 算法2.Hitchhiker-LRC+的数据分配算法 输入:k、r、p、A. Step 1.计算p,q的值. 执行公式(2). Step 2.附加p×(r-1-q)数据到前r-1-q校验上. FORi=0;i pi=pi⨁f2(ap×i+1,ap×i+2,…,ap×i+p) END FOR Step 3.附加(p+1)×q个数据到P中的后q个校验上. FORi=r-1-q;i pi=pi⨁f2(ap×i+1,ap×i+2,…,ap×i+p,ap×i+p+1) END FOR 首先按照公式(2)计算p,q的值;其次给P中的前r-1-q个校验附加p个A中的数据;然后给P中的后q个校验附加p+1个A中的数据;最后保证每一次附加的数据都是Q中后r-1个校验中的同一个校验的局部校验.按照上诉方法k个数据将完整的捎带在p中的校验上. 以(k=10,r=4)作为编码的例子,其中l=r=4.第1步计算校验并分配捎带数据.按照RS(10,4)的编码方式计算校验,将10个数据编码得到4个线性无关的校验.接着按照算法2来分配捎带的数据,其中p=3,q=1,即P中的前2个校验存储3个A中的数据,最后一个校验存储4个A中的数据.如图6(a)所示.第2步和第3步的编码方式与Hitchhiker-LRC相同,不再赘述,分别如图6(b)、图6(c)所示. 3.2.3 解码过程 与Hitchhiker-LRC相比,Hitchhiker-LRC+的解码过程相对简单.A和B中数据的恢复只与校验P有关,与校验Q无关;同理,校验的恢复只与校验Q和P中捎带的A中的数据有关,与A中其他数据无关.由于所有的数据都捎带在P中,所以数据的解码只有一类,同Hitchhiker-LRC,将其称为dr型.校验单元同样还是pn型、ps型和pa型这三类.数据单元和校验单元的解码方法均可按照算法1中的方法解码.对数据单元而言,没有dl类型,因此在算法1中的Step 1进行类型比较时,不需判断数据单元的类型,其均为dr类型.由于前r-1-q个校验与后q个校验中捎带的数据量不同,因此下载A中数据的数量不同.前p×(r-1-q)个数据单元的恢复与算法1中的dr相同;后q×(p+1)个数据单元的恢复则需多下载一个帮助的数据,由原来的p-1增加到现在的p.即将原来的ai|i∈{p×p′+1,…,p×p′+p}{x}替换成现在的ai|i∈{p×p′+1,…,p×p′+p+1}{x},将原来的fp′+2(b)⨁f2(ai)|i∈{p×p′+1,…,p×p′+p}替换成现在的fp′+2(b)⨁f2(ai)|i∈{p×p′+1,…,p×p′+p+1}.对校验单元而言,三种类型都不需下载A中余下的q个数据,即不需要下载ai|i∈{p×p′+1,…,p×p′+q}{x}(pn所需)和ai|p×(r-1)+1,…,p×(r-1)+q}{x}(ps和pa所需). 图6 Hitchhiker-LRC+(10,4)编码示意图 当单元失效时,修复该单元的平均下载量占原数据总量的百分比,称为修复带宽率γ. (5) (6) 图7 Hitchhiker-LRC+(10,4)解码方式 其中δ为总修复下载量,是修复每个单元所需下载的帮助数量之和. δ=δsys+δpar (7) 4.1.1 Hitchhiker-nonXOR (8) 4.1.2 Hitchhiker-LRC (9) 4.1.3 Hitchhiker-LRC+ (10) 让参与编码的码字都在有限域GF(2t)内,为方便分析,假设加法或减法的时间复杂度为O(t),乘法的时间复杂度为O(t2)[25].实际上,一个(k,r)的MDS码,生成一个校验或修复一个系统节点需要k次乘法和k-1次加法.分析每种编码的编码时间复杂度和平均解码时间复杂度. 4.2.1 编码的时间复杂度 a)Hitchhiker-nonXOR共有2r个校验,其生成有三步,分为捎带前、捎带和横向减法.捎带前即为产生一个(k,r)的MDS码,那么生成2r个校验的时间复杂度为O(2r(kt2+(k-1)t)).第二步为捎带,每个节点捎带p个数据,可看做(p,1)的MDS码,时间复杂度为O(pt2+(p-1)t).其计算的结果还需与捎带位置的校验相加.一共有r-1个节点需捎带数据,因此,捎带的时间复杂度为O((r-1)(pt2+pt)).剩下的横向减法的时间复杂度为O(t).所以,Hitchhiker-nonXOR的编码时间复杂度为O(2r(kt2+(k-1)t)+(r-1)(pt2+pt)+t). b)Hitchhiker-LRC的是在Hitchhiker-nonXOR横向减法之前多了求局部校验这一步,其余步骤相同.一共有r个校验参与,也就是把r个校验相加,其时间复杂度为O(r-1).所以Hitchhiker-LRC的编码时间复杂度为O(2r(kt2+(k-1)t)+(r-1)(pt2+pt)+t+r-1). c)Hitchhiker-LRC+与Hitchhiker-LRC的不同点在于捎带的方式.该方式是前r-1-q个校验捎带的是p个数据,后q个校验捎带的是p+1个数据.可分别看做(p,1)的MDS码和(p+1,1)的MDS码,再加上与捎带位置的校验的加法的时间复杂度,得到捎带的时间复杂度为O((r-1)(pt2+pt)+q(t2+t)).所以,Hitchhiker-LRC+的编码时间复杂度为O(2r(kt2+(k-1)t)+(r-1)(pt2+pt)+q(t2+t)+t+r-1). 4.2.2 解码的时间复杂度 解码分为数据单元和校验单元,其中第一个子条带与第二个子条带也分开计算. (11) (12) (13) Hitchhiker-LRC和Hitchhiker-LRC+两种编码的修复带宽率都会随着r的增加渐渐次于原Hitchhiker码.归其原因为两种编码都让第一个子条带中的全部校验都参与了局部校验的计算.若想让r的增大不直接影响修复带宽率,可让参与局部校验的数量l随着r的增加而减少.这样在修复某一个校验单元的时,下载的帮助节点变少.当然,如果参与局部校验的数量太少,采用LRC的方式降低校验节点的修复带宽也不明显.因此对于任意一个(k,r)的参数取值,都存在l,使得两种编码的修复带宽达到最优,其中2≤l≤r.通过分析Hitchhiker-LRC+的解码过程,得到l动态变化后的总修复下载量δhl+如公式(14)所示. (14) 其中k,r,q,p已知,且k>0,2≤r 本文在HDFS-RAID中实现了Hitchhiker-LRC和Hitchhiker-LRC+两种编码,通过策略的方式添加到HDFS中,称这两种策略分别为HDFS-HHLRC和HDFS-HHLRC+.根据实验结果,对比分析Hitchhiker-nonXOR、Hitchhiker-LRC和Hitchhiker-LRC+这三种编码的修复带宽率. 实验部署在分布式系统集群中(Hadoop),集群中由1个NameNode节点和19个DataNode节点组成.所有的节点运行在Ubuntu16.04系统和JDK1.8中,其中每个节点配置2个8核Intel 2.5GHz处理器,48G RAM,2T硬盘和2GB/s以太网卡.实验数据为500个640M文件,保持默认HDFS的数据块大小64M,编码有限域选择GF(28)设置不同(k,r)参数来分析三种编码的修复带宽率. 通过实验,并结合4.1节中的公式,观察k与r的关系.图8(a)描绘在k=10,r={3,4,5,6,7,8}时,三种编码 Hitchhiker-nonXOR、Hitchhiker-LRC和Hitchhiker-LRC+的修复带宽率.将Hitchhiker-nonXOR码作为修复带宽率的上界,不难看出,当2≤r 图8(b)描述的是当2 图8(c)是工业界中常用的参数配置(k,r)=(5,2),(6,3),(8,4),(10,4)时Hitchhiker-nonXOR、Hitchhiker-LRC和Hitchhiker-LRC+修复带宽率对比图.图8(c)中可发现Hitchhiker-LRC+始终保持最低.在参数(k,r)=(5,2),(6,3)时Hitchhiker-LRC和Hitchhiker-LRC+码相比于Hitchhiker-nonXOR的修复带宽率都降低了4.2%.在参数(k,r)=(8,4)时,Hitchhiker-LRC因r的增加,修复带宽率高于Hitchhiker-nonXOR和Hitchhiker-LRC+;Hitchhiker-LRC+的修复带宽率最低,相对于Hitchhiker-nonXOR降低了2.5%,相对于Hitchhiker-LRC降低了5.2%.在(k,r)=(10,4)时,Hitchhiker-LRC相比于Hitchhiker-nonXOR降低了1.7%;而Hitchhiker-LRC+码相比于Hitchhiker-nonXOR降低了2.5%. 图8(d)是工业中常用的参数配置(k,r)=(5,2),(6,3),(8,4),(10,4)时Hitchhiker-nonXOR、Hitchhiker-LRC和Hitchhiker-LRC+编码时间开销.三种编码在这四种参数配置上的时间开销相互持平,在(k,r)=(5,2)时Hitchhiker-LRC和Hitchhiker-LRC+比Hitchhiker-nonXOR高0.0056%.在(k,r)=(6,3)时Hitchhiker-LRC和Hitchhiker-LRC+比Hitchhiker-nonXOR高高0.0067%,在(k,r)=(8,4)时,Hitchhiker-LRC比Hitchhiker-nonXOR高0.006%;Hitchhiker-LRC+比Hitchhiker-nonXOR高0.29%.在(k,r)=(10,4)时,Hitchhiker-LRC比Hitchhiker-nonXOR高0.0047%;Hitchhiker-LRC+比Hitchhiker-nonXOR高0.12%. 图8(e)是工业中常用的参数配置(k,r)=(5,2),(6,3),(8,4),(10,4)时Hitchhiker-nonXOR、Hitchhiker-LRC和Hitchhiker-LRC+解码时间开销.在参数(k,r)=(5,2)时,Hitchhiker-LRC和Hitchhiker-LRC+的解码时间开销略低于Hitchhiker-nonXOR;在(k,r)=(6,3),(8,4),(10,4)时,Hitchhiker-LRC和Hitchhiker-LRC+的解码时间开销略高于Hitchhiker-nonXOR. 图8(f)是工业中常用的参数配置(k,r)=(5,2),(6,3),(8,4),(10,4)时Hitchhiker-nonXOR、Hitchhiker-LRC和Hitchhiker-LRC+修复时间开销(传输时间+解码时间).根据图8(f)可知,除了在(k,r)=(8,4)时Hitchhiker-LRC比Hitchhiker-nonXOR的修复时间高,其余参数下Hitchhiker-nonXOR的时间都是最高.实验证明网络开销是Hadoop等平台的主要瓶颈,增加少量的计算时间,可节省更多的传输时间,达到降低整体时间的目的. 图8 不同k,r的总修复带宽率、编码时间、解码时间和修复时间 本文通过对原Hitchhiker的部分校验求局部校验,并让其存放的位置做横向减法的方式,构造出两种新的编码Hitchhiker-LRC和Hitchhiker-LRC+.这两种编码在2≤r2 相关理论基础
2.1 定义

2.2 LRC
2.3 Hitchhiker码
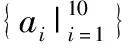


3 改进的Hitchhiker码
3.1 Hitchhiker-LRC码
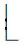

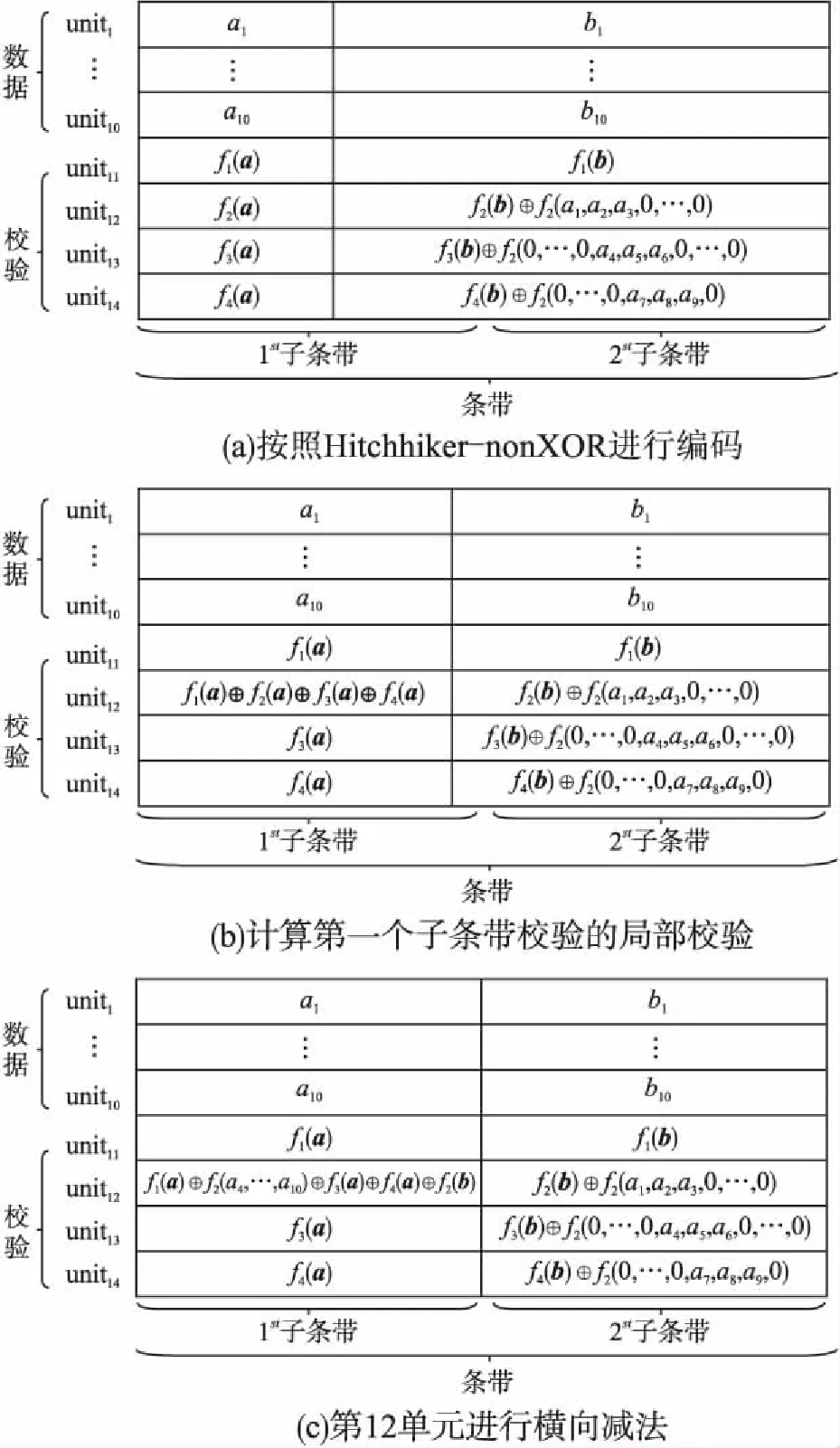
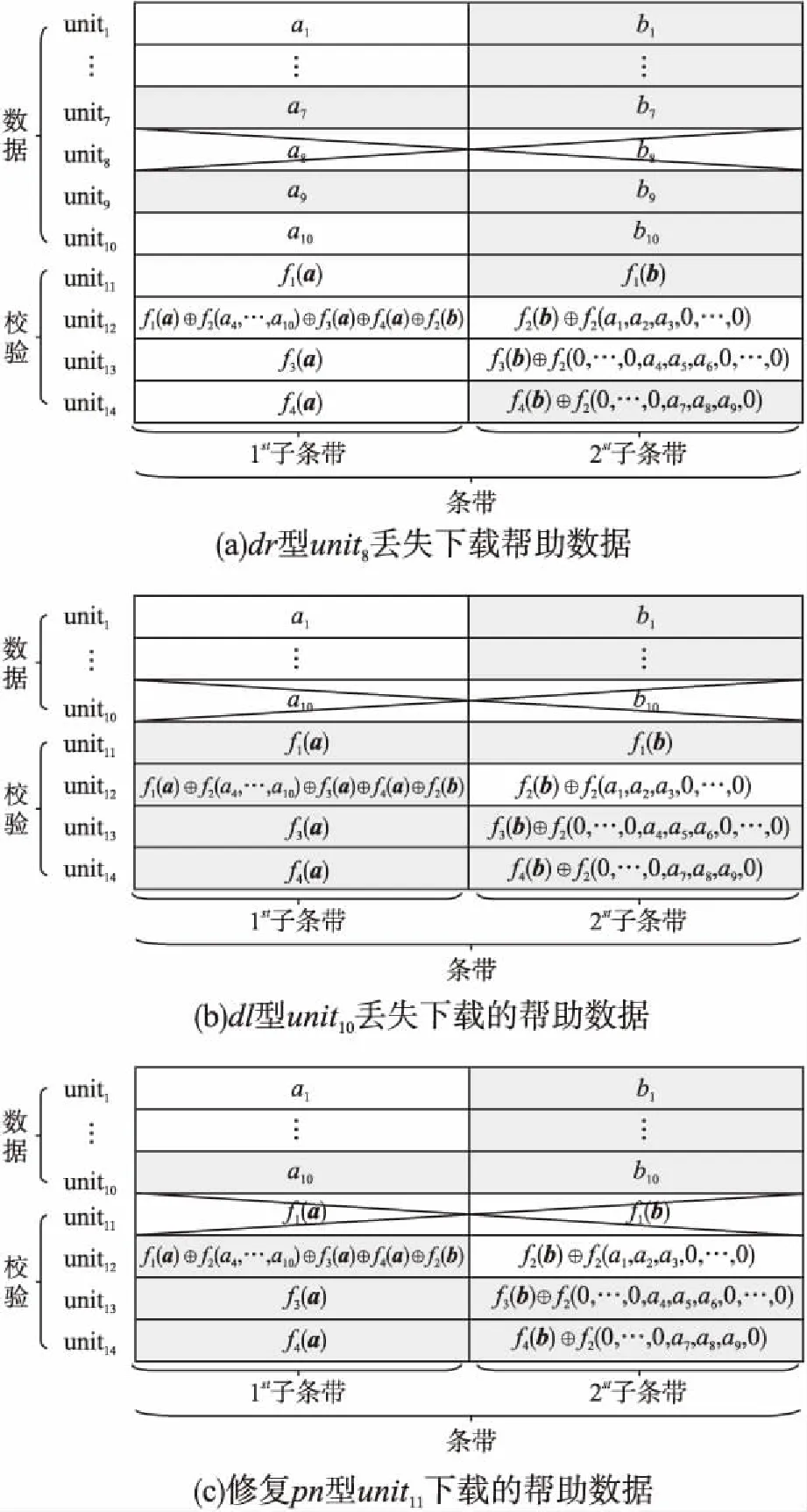

3.2 Hitchhiker-LRC+码

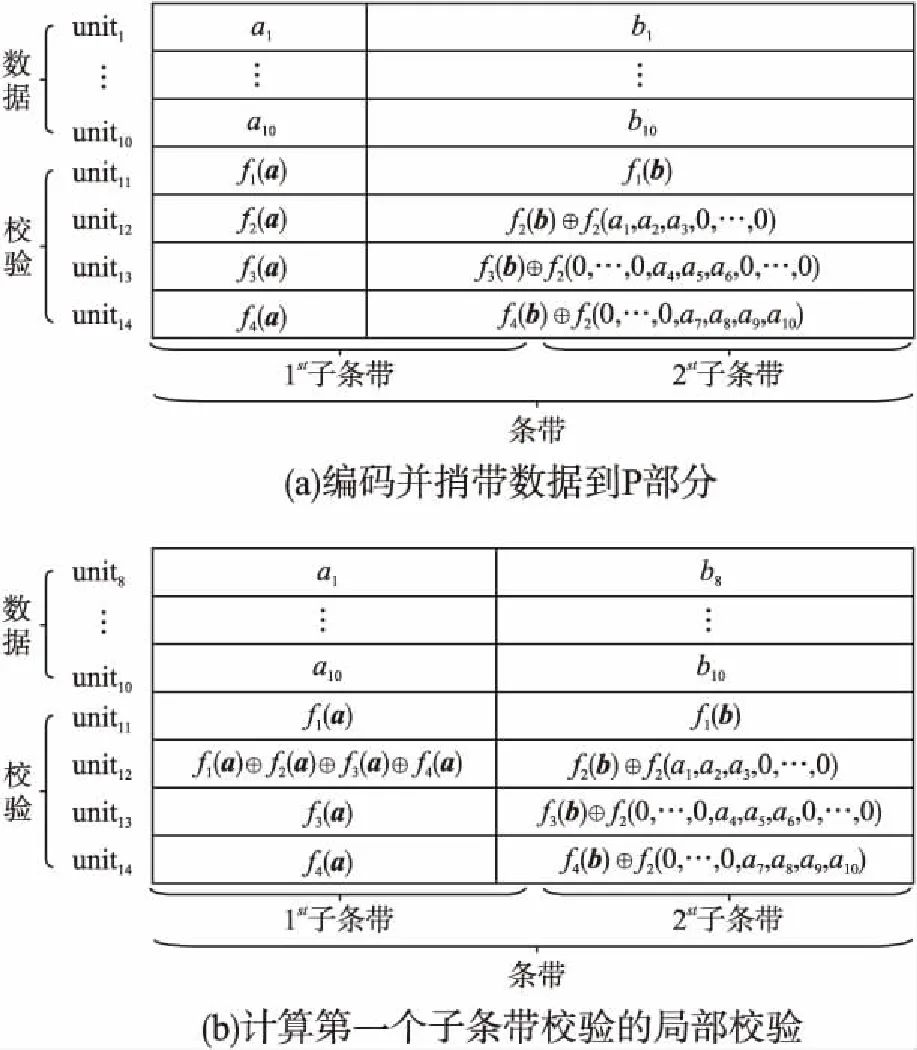

4 理论分析
4.1 修复带宽率
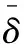
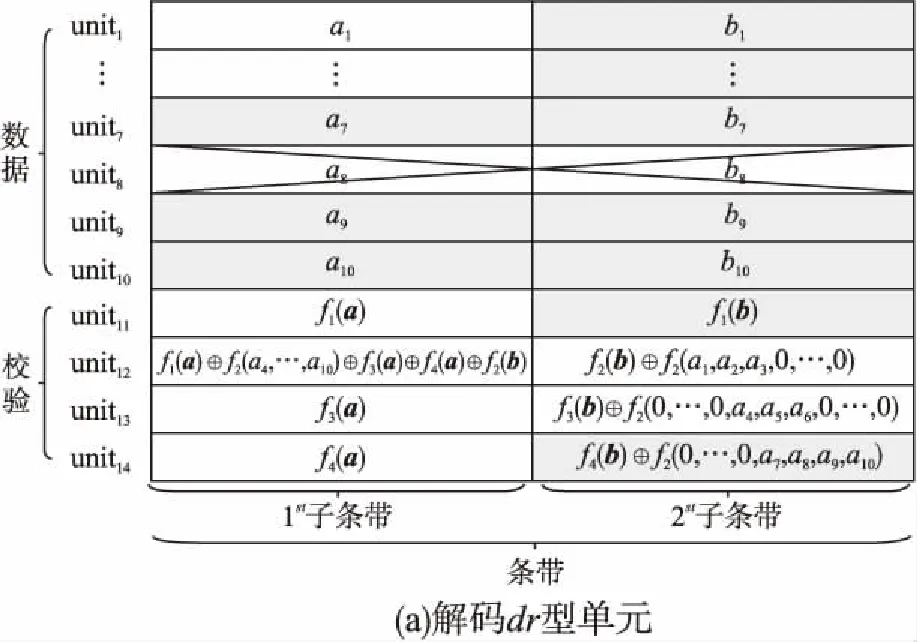

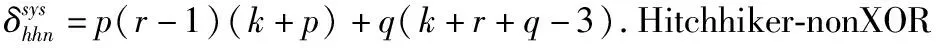
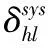
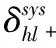
4.2 编码与解码的时间复杂度


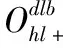
4.3 (k,r)的最优修复带宽率
5 实验分析
5.1 实验平台
5.2 实验结果
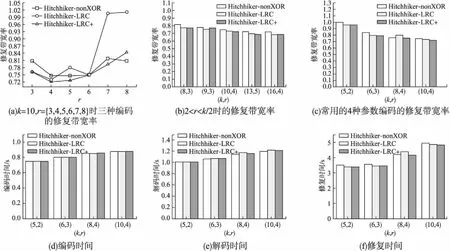
6 结束语
