上流式厌氧反应器进水结构数值模拟分析

李欣欣，黄 河，黄科学，肖延安，陈文贤

广西大学机械工程学院，广西 南宁 530004

布水器作为上流式厌氧反应器的主要结构之一，其作用是将废水注入至反应器内部，并通过水流产生的水力搅拌作用，使污水与反应器中的污泥充分混合，以净化污水。布水器的结构直接影响反应器内部污水中的有机物与污泥颗粒接触的均匀程度。良好的布水器结构能够有效地提升影响污水的反应速度，减少死区，提高污水处理效果。

目前厌氧反应器布水器根据流动方式不同分为点、线及面布水器[1]。点布水器分为单点及多点布水，其结构简单，操作方便，但易出现偏流和配水不均匀的情况。多点布水相对于单点布水，由于布水孔分布较多且均匀，配水均匀度有所改观。线布水器可实现沿管长方向均匀布水，但垂直方向依旧较差[2]，且结构较为复杂。面布水器由于出口压力过小而易堵塞。因此，对于上流式厌氧反应器，本工作综合经济、方便和实用性考虑，采用水平排管、多喷口线性布置的结构，并对进水均匀度进行研究以优化结构参数[3-7]。

随着近年来流体力学与计算流体力学（CFD）的发展，越来越多的国内外学者将其应用于厌氧反应器的结构优化设计中[8-13]。本工作针对某上流式厌氧反应器布水器部分的简化模型，使用CFD软件Fluent对进水情况进行三维数值模拟仿真，分析进水管内径（d）、进水喷口密度（ρd）及喷管安装角度（α）3个因素对其进水均匀度的影响，为上流式厌氧反应器的布水器结构优化设计及工程应用提供参考。

1 实验部分

1.1 进水结构的模型建立

计算模型是根据某上流式反应器简化而成。反应器为地上立式圆柱体，底部为平面，反应器直径（D）为3.45 m，反应器高度（H）为1.55 m。进水管中心线位于距底部高度（h）为0.55 m处平面内，平行于底面的某平面高度为h1，喷口轴线与XOZ平面所成锐角为α。整体简化模型如图1。进水管模型如图2。两根支管与反应器直径边界的距离比（L1:L2:L3）为1:2:1；同时，将反应器内部设置为充满液体状态；出口设置在高度为1.55 m处的模型顶部；另外，为方便分析进水结构影响，暂不考虑反应器内部其他结构。

图1 反应器简化模型及参数示意Fig.1 Simplified model and parameters of the reactor

图2 进水管布置建模Fig.2 Distributor model

1.2 数值模拟计算

1.1.1 实验设计

影响反应器进水均匀度的主要因素有：进水管内径（d，如图1所示）、进水喷口密度（ρd，以单根进水管在反应器3.45 m直径中喷口个数代表进水喷口密度）和喷口安装角度（α，如图1所示）。本实验中污水的含固率约为10%，黏度经测试为0.032 975 Pa·s，属于低黏度液体，因此计算过程中将污水整体简化为单相低黏度不可压缩液体。保证污水水力停留时间一定，即保证进水流量一定，以进水管内径、进水喷口个数和喷口安装角度作为实验的3个影响因素。

1.1.2 网格划分及网格无关性验证

Fluent提供了多种非结构化网格划分方法，如curvature方法、proximity方法及advance方法。curvature网格划分方法是从孔的外周开始划分，以最小角度或最小网格为最初网格大小，并以所设定的增长率作为网格大小增长速率，直至网格大小达到设定的最大网格尺寸或最大面网格尺寸，这样可较好地满足网格细化的要求。本实验中由于内径、喷口直径与整体模型尺寸差距较大，且支管与喷口分布不对称，网格划分需将进水区域附近进行细化。因此，采用curvature方式划分网格，以非结构化网格对几何体进行网格划分，并在反应器壁面与进水管壁面附近添加膨胀层。

为了验证网格无关性，将模型网格数量增加后进行对比。模型网格数量增加将近一倍，但速度云图变化并不明显，如图3所示。网格数量及评估指标比较如表1所示。由于图3（c）中最小网格尺寸较小，有助于得到较为精确的仿真结果，因此选取230×104网格设置作为仿真网格设置，模型网格分布如图4所示。

图3 不同网格数量结果速度云图Fig.3 Velocity contours of different mesh

图4 反应器三维网格结构Fig.4 Three dimensional grid structure of the reactor

表1 不同网格数量的评价指标表Table 1 Evaluation indexes of different mesh settings

1.1.2 求解设置

本实验模型使用Fluent的有限体积法求解，采用适合预测自由剪切流动的标准k-ε湍流模型来细化计算喷口处的速度变化；使用黏度和密度均与污水相近的、不可压缩的液体作为计算时的工作流体，黏度设置为0.03 Pa·s，密度为1 000 kg/m³；考虑到反应器的安装情况与液体的自重方向，设置Y轴负方向为重力方向，重力加速度为9.8 m/s²；采用收敛速度较快的压力–速度耦合SIMPLEC算法，选用二阶迎风式，并且适当调小压力松弛因子，进一步确保收敛速度。连续性的残差值设定为小于1×10-3，各方向的速度残差小于1×10-4时认定为收敛。

1.1.3 边界条件

为保证反应器中污水停留时间恒定，对于不同直径的进水管设置不同的入口速度，具体可见表2。进口压力设置为10 000 Pa，出口压力设置为0 Pa。

表2 入口速度Table 2 Inlet velocity

2 评价指标确定与参考平面选择

2.1 评价指标确定

良好的布水器结构能够有效地提高进水均匀度，并有效减少反应器底部的沉降死区。文献[13]使用上升速度变异系数来评价进水均匀度，计算式如式（1）。

式中：MF为速度变异系数；n为采样点数；Vy为上升速度，m/s；Vy为上升速度平均值，m/s。

由于本实验整体速度较小，造成变异系数也较小，数据结果不直观，因此采用上升速度变异系数的倒数作为进水均匀度的评价指标，如式（2），指标越大，上升速度偏离程度越小。

2.2 参考平面选择

为了评价进水均匀度，需要选择一个较为合适的参考平面作为评价指标计算的平面。设距离反应器底面的高度为h1，以h1为0.65，0.75，0.85和0.95 m等4个高度位置的平面（即距进水管中心线所在平面0.1，0.2，0.3和0.4 m处水平面）作为速度采样平面，并在各平面内等间隔取600个采样点，计算上升速度变异系数的倒数，以评价布水器的进水均匀度。仿真条件如表3所示。

表3 实验参数设计Table 3 Design of test parameters

根据图5（a）可知，随着旋转角度从0°增大到50°，各水平面上评价指标的变化趋势基本一致，先上升后下降，并在30～40°达到最高值。由图5（b）可知，随喷口密度的增多，各水平面上评价指标变化趋势基本一致，评价指标随喷口密度增长而增长。

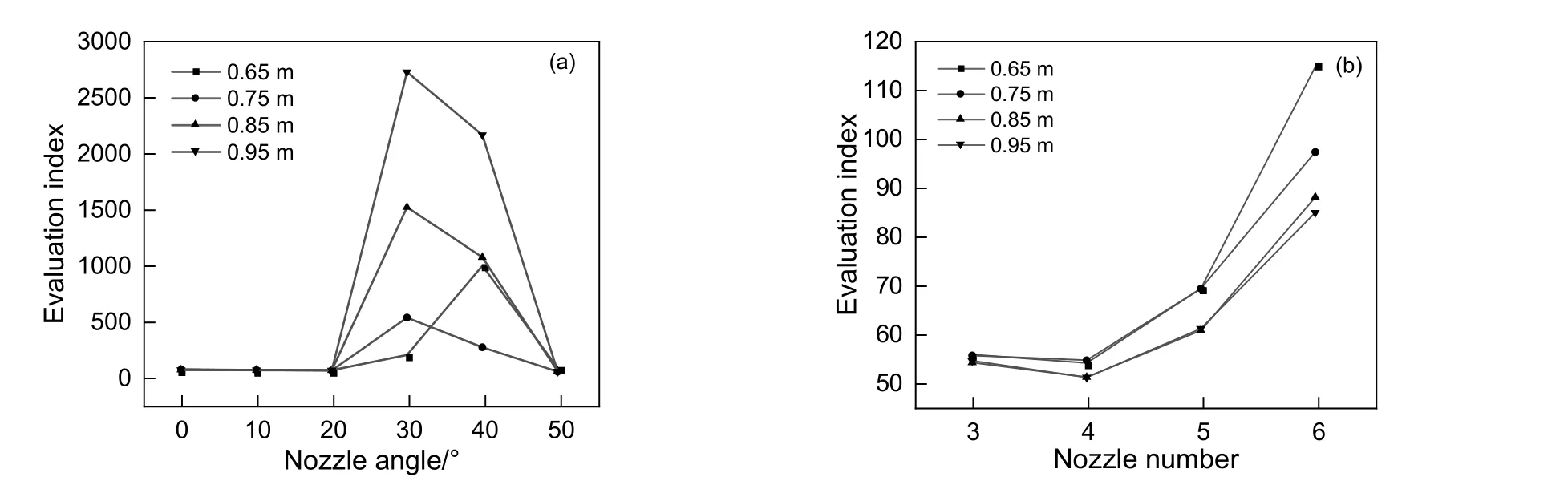
图5 不同高度评价指标随参数变化情况Fig.5 Effect of different height on evaluation indexes

由于在进水喷口参数变化过程中，进水喷口在长度方向上会穿透h1为0.65 m和0.75 m水平面，无法进行均匀度分析，导致h1为0.85 m和0.95 m水平面上评价指标变化趋势近乎一致，为了探寻进水结构对均匀度影响，在不影响结果的情况下，参考平面不宜过高。综上所述，选取0.85 m水平面处作为进水均匀度的参考平面，参考平面内上升速度的变异系数的倒数作为进水均匀度评价标准，其值越大表示均匀度越好。

3 单因素分析

对已建立的布水器结构模型，进行单因素分析，分析进水管内径、进水喷口密度及喷管的安装角度3个因素，对进水均匀度的影响。

3.1 实验设计

原设计中管内径为150 mm，考虑到成本问题，采用与其相近的标准钢管管径，其内径与公称直径参照表2。考虑喷口分布关于反应器轴线中心对称，因此喷口安装角度取值为0，10，20，30，40和50°；喷口密度取值为3，4，5和6。

单因素实验方案如表4所示。

表4 实验参数设计Table 4 Design of test parameters

3.2 单因素结果分析

由图6（a）图可知，当喷口密度由3增长至6时，评价指标不断增大，上升速度方差不断减小，均匀度逐渐提升喷口密度增加有利于流体均匀分布，密度越大布水均匀度越高；根据图6（b）可知，随着进水管内径由110 mm增到227 mm，评价指标波动较大，进水管内径增大对流体均匀度有一定的影响；从图6（c）可知，随着喷口旋转角度从0°到50°逐渐增大，评价指标先升后降，在20°后开始上升，并在30～40°升至最高；当喷口旋转角度大于40°，则均匀度快速下降；可知，进水均匀度随喷口旋转角度增大，先增加后减少，在20～40°变化显著，并在30～40°到达最佳效果，流体均匀度最高。

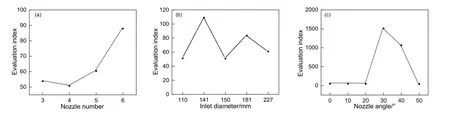
图6 不同因素对进水均匀度评价指标的影响Fig.6 The impacts of different factors on evaluation index

4 多因素正交分析

4.1 因素水平的确定与正交表设计

由上述单因素分析可知，进水喷口密度（A）、水管的直径（B）及喷管的安装水平角度（C）3个因素对进水均匀度均有不同程度的影响。基于单因素分析，正交实验因素的合适范围为：喷口密度为3～6，进水管内径为110～141 mm，喷口安装角度为10～40°。3因素实验因素的水平一般在3～6水平，为在满足分析要求情况下尽量减少实验次数，因此每个因素都取4个水平，本实验的因素水平如表5所示。

表5 因素水平表Table 5 Test factors and levels table

在满足上述条件情况下，保证实验次数最小并尽量选择标准正交表。其中常用正交表中可选择3因素4水平正交表L16（43），可完全包容因素水平表且实验次数最小。形成如表6的实验方案。

表6 正交实验设计方案Table 6 Parameters of the orthogonal tests

4.2 实验结果分析

通过对正交表当中的模型参数，建立3D模型并进行数值模拟分析，得到反应器在高度为0.85 m平面内上升速度变异系数的倒数。并利用得到的数值通过正交软件单变量分析可得到实验数值的均值、极差和方差分析等数值，结果如表7和表8所示，其中，K1，K2，K3和K4为各水平结果总和，代表其影响程度，R为极差，DOF为自由度，F表示显著性。

表7 正交实验结果Table 7 Orthogonal result

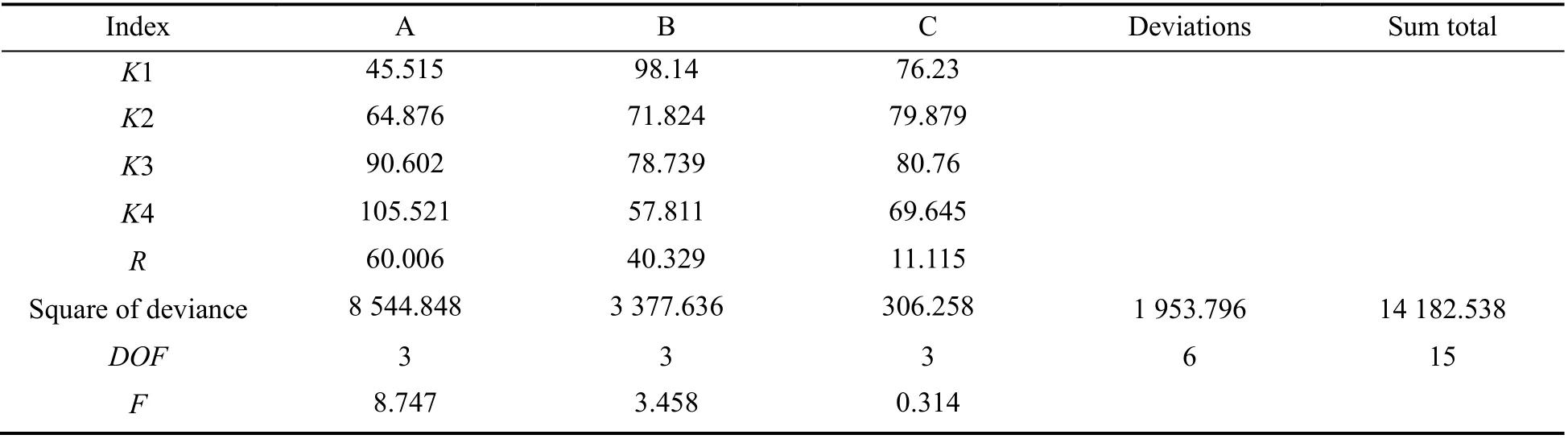
表8 正交实验分析Table 8 Orthogonal test analysis

在进水流量一定的情况下，评价指标越大，上升速度变异系数越小，代表进水均匀程度越高。通过极差与方差分析可知，3个因素对评价指标的影响从大到小依次为A，B和C，为了清晰地体现水平变化对评价指标的变化，绘制各因素水平的影响均值如图7所示

图7 3个因素的效应曲线图Fig.7 Effect curves of three factors

由图可以看出，与单因素实验结果表现一致，评价指标随喷口密度上升而上升，随进水管内径上升而下降，随喷口安装角度增大先增后减。且在喷口密度为6，进水管内径为110 mm，喷口安装角度为30°时，评价指标最大，即A4B1C3为最优组合。

5 最优方案的对比分析

根据上述正交实验结果，得到的最优方案：喷口密度为6，进水管内径为110 mm，喷口角度为30°。根据最优方案参数建立模型，并进行数值模拟，计算其进水均匀度评价指标值，结果见表9。由表可知，最优方案的进水均匀度大于正交实验最优组，说明最优方案比正交实验最优组能更有效地提高进水均匀度。

根据原设计方案参数，即喷口密度为4，进水管内径为150 mm，喷口角度为0°，可计算出其进水均匀度指标值，如表9所示。截取原设计方案和最优方案的3个高度平面，得到其上的上升速度云图，分别如图8和图9所示。

表9 评价指标对照表Table 9 The comparison of evaluation index

图8 原设计方案不同高度平面上水流上升速度分布Fig.8 Velocity contours of original design on different height planes

图9 最优方案不同高度平面上水流上升速度分布Fig.9 Velocity contours of optimized design on different height planes

由仿真计算进口条件设定，图8和图9各高度截面入口流量一致。由图8可知，原设计方案中存在较大范围高上升速度区域（黄色及以上），约占总面积的6%；各高度截面的较高流速区域均集中在反应器两侧，在反应器中央则上升速度较低，进水分布均匀度不高。由图9可知，最优方案的各高度平面上水流上升速度的最大值虽然没有原设计方案的大，但可以看到在中间区域，水流上升速度了比原设计方案有了提升，这有助于提高布水的均匀度。

综上所述，最优方案比正交实验最优组、原设计方案能更有效地提高进水均匀度。

4 结 论

针对上流式厌氧反应器的进水过程，利用Fluent软件，对不同结构参数的布水器进水情况进行数值模拟，分析各因素对进水均匀度的影响规律，得到以下结论：

a）喷口密度对进水均匀度的影响最大，进水管内径的影响次之，喷口安装角度影响最小；

b）改变喷口安装角度能有效减小流体在反应器两侧聚集，同时减小反应器两侧速度，提高进水均匀度，且在角度为30°时效果最佳；

c）喷口密度对进水均匀度影响较大，大的喷口密度有利于提升进水均匀度；

d）进水管内径大小对进水均匀度有影响，进水管内径从141 mm降至110 mm过程中进水均匀度得到提升；

e）优化方案：喷口密度为6，进水管内径为110 mm，喷口安装角度为30°。