枪弹间隙对水下枪内弹道的影响

孟祥宇，侯 健，秦一平，廖 斐，鲁春佳

（海军工程大学，湖北 武汉 430000）

现阶段，水下枪炮发射主要采用密封式或全水下式发射[1-3]，这两种发射方式均存在一定的局限性。由于水下射弹受到水动压力的影响，膛内运动时受阻力较大，采用全水下式发射时存在过量弹前载荷导致膛压较高的问题，为了保证枪管的安全性，往往减少装药，造成射弹初速较低。而采用密封式发射能够保证良好的密封性能，防止大量海水进入枪管，减小弹前载荷，降低弹头在内弹道期间的运动阻力，保证发射安全性和初速，但该发射方式在射击中断后会产生液体回流现象，需要排出身管内的海水，再次密封炮口，结构复杂且射速较慢。为了提高射速，克服全水下发射的高膛压缺陷，在全水下发射的基础上，通过优化枪弹间隙配合，使部分火药燃气通过间隙，生成气幕推动弹前水柱加速排出炮口，从而消除附加质量对超空泡射弹发射的影响，有效地减小膛压，提升射弹初速度。

水下气幕由多股燃气射流汇聚生成，有关气体射流与水相互作用的问题，相关学者进行了较多研究。Hoefele 等[4]用高速摄影和压力测量的方法研究了气体分别通过直线型和扩张型风嘴喷入液体时的流场。Mori 等[5]优化了风嘴运行的工作条件，发现随着射流速度的增加，气泡敲击频率降低，可以实现泡状流向射流的转变。施红辉等[6]对超音速射流胀鼓和回击特性进行了试验研究，结果表明胀鼓频率越高，回击频率越高。薛晓春等[7-10]以整装式液体发射药（BLPG）火炮多点点火为背景，针对渐扩型圆柱观察室开展了双束及四束燃气射流与液体工质相互作用的数值仿真与实验研究。Weiland 等[11]研究了圆形射流入水过程中气液边界动力学特性与气液作用稳定性的关系。陈启林[12]针对水下燃气射流流动过程、压力特性和噪声特性进行了研究，并利用 FW-H 噪声预报模型对水下超声速燃气射流的噪声进行了模拟计算。汤龙生等[13]针对水下超声速燃气射流气泡的生长及压力波传播特性进行了实验研究，结果表明燃气泡生长和 “破碎”伴随着压力脉动在水介质中传播，气泡压力波的能量在水介质中快速衰减。

目前，对气体射流与水相互作用的研究主要侧重于流场特性及射流汇聚过程，国内外有关水下气幕式发射的研究也主要集中在导弹水下发射领域，通过实验研究与数值分析，获得导弹水下气幕式发射过程的流场特性。针对枪炮在全水下环境利用气幕优化发射过程的研究较少。南京理工大学周良梁等[14-15]设计了相关实验，建立了多股燃气射流在充液圆管中扩展的三维非稳态数理模型，研究了枪炮水下气幕式发射过程中喷射结构和喷头运动对气幕特性的影响。赵嘉俊等[16-18]分析了锥形分布的多股燃气射流在柱形充液室内的扩展特性，得到了不同结构及喷射压力情况下射流形成的Taylor 空腔和流场内回流区的演化特征。

本研究基于水下枪全水下发射机理，针对枪弹间隙配合技术特点，探讨过间隙气体生成的气幕对水下枪全水下发射内弹道的影响，运用AUTODYN 有限元软件对有无间隙和不同装药量条件下的内弹道过程进行数值仿真，设计水下实弹射击实验，采用实验和数值仿真相结合的方法对比分析气幕的生成对射弹在内弹道过程运动的优化作用，以及不同装药量对水下枪发射内弹道特性的影响。

1 水下枪带间隙发射物理模型及状态方程

1.1 物理模型

水下枪完全浸于水中，发射射弹时利用枪弹配合的间隙使弹后空间的部分燃气以射流的方式在枪管内形成气幕，从而达到协同排水的目的。通过将发射环境由液体变为低压气体，能够减少弹丸在膛内前进过程中水对其产生的阻力，可避免现有发射方式的不足。发射过程如图1 所示，其中：lg为弹丸全行程，ld为弹丸长度，l为弹丸在膛内运动位移，ly为过间隙气体流出量等效长度。

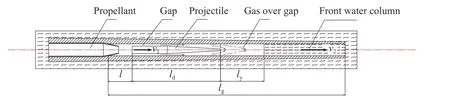
图1 水下枪枪弹耦合带间隙发射物理模型Fig. 1 Physical model of underwater gun-bomb coupling gap launch

1.2 基本假设

高温高压燃气过间隙流动及其射流在膛内液体中扩展的过程非常复杂。在不失其流场基本特征的情况下，针对燃气射流扩展过程作如下简化[14-18]：

（1）燃气射流过间隙后不再发生化学反应且组分保持不变；

（2）考虑到高温燃气与液体介质作用时间短暂，忽略液体汽化影响；

（3）间隙控制在0.1 mm 以内，不考虑弹丸振动的影响。

1.3 状态方程

1.3.1 发射药状态方程

发射药燃烧与爆轰有本质差别。随着燃烧的进行，燃烧室内的气体压力不断增加，燃烧速度也不断增大，与炸药基本具有稳定爆速截然不同，因此在使用AUTODYN 模拟火药燃烧时使用JWL 状态方程并不能符合实际。本研究采用Powder Burn 模型（慢燃烧模型）对发射药燃烧进行仿真。在确定慢燃烧模型的材料数据时，对慢燃烧数学模型的清晰认识具有重要意义。

慢燃烧模型由固体状态方程、反应比方程和反应产物的气体状态方程组成。通过发射药质量ms随时间t的变化可以得到反应比方程

反应产物的气体状态方程（EOS）使用指数状态方程

式中：ρg为气体密度，eg为气体质量内能，D为常数，pg为反应产物气体压力。

指数状态方程得出了反应产物气体压力pg，将气体压力带入Vieille 定律公式可以得到固体的燃烧速率

式中：b为固体的燃烧速率，a、n、C为常数。

通过反应比W、固体燃烧速率b和几何形状参数可以确定反应速率公式

式中：G为生长参数，α为反应比因子，c为生长反应比指数。G、α和c由发射药形状确定。本研究使用的发射药为5/7 石发射药，该种药型为7 孔柱形发射药，参数列于表1，其中ρref为参考密度，ρs为发射药密度，Tref为参考温度，κ为热导率。

表 1 发射药材料参数Table 1 Material parameters of propellant

1.3.2 水的状态方程

水的状态方程使用Polynomial 状态方程，其本质是 Mie-Grüneisen 高压状态方程，不过是将冷压和冷能以及Grüneisen 系数表示成多项式的形式。AUTODYN 程序中的Polynomial 状态方程如下

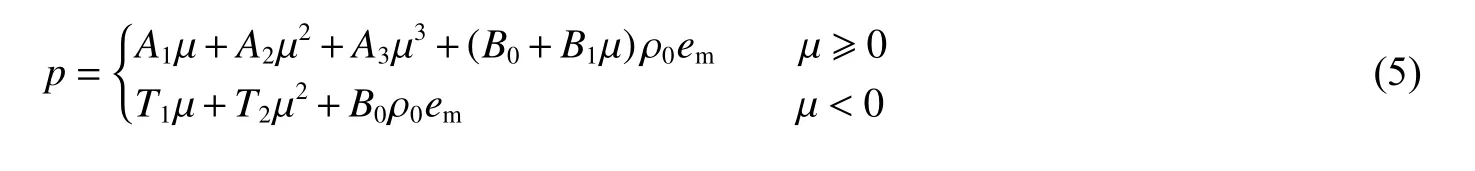
式中：em是单位质量内能增量，µ为压缩度（代表水受拉或受压状态），A1、A2、A3、T1、T2为压强量纲常数，B0、B1为无量纲常数。具体参数取值列于表2。

表 2 AUTODYN 程序提供的水多项式状态方程参数Table 2 The polymerization EOS parameters of water provided by the AUTODYN program

2 边界条件与计算模型

2.1 计算域

水下枪发射装置主要由水下发射自动机和枪管组成。在水下枪的内弹道仿真过程中，枪体全部浸入水中，身管内充满液体，是燃气与液体相互作用的主要区域。此外，还包括火药燃烧的药室区域以及枪口附近液体区域。由于不考虑弹丸在枪管内的振动，选取1/2 截面作为仿真的计算域，如图2 所示。

图2 水下枪带间隙发射计算域Fig. 2 Computational domain of underwater gap launch

2.2 网格划分与无关性验证

由于本研究不对弹丸、弹壳及枪管的变形进行分析，因此将其设置为刚体，使用Lagrange 网格。两相流模型采用Euler-Euler 算法求解，因此火药燃气及水介质等流体区域采用Euler 网格划分，划分时将发射药与空气填充至水的Euler 域中，结构长度与实际尺寸相对应。膛口流场区域取长为0.5 m、半径为0.2 m 的圆柱形区域。

对膛口流场和弹丸运动轨迹区域进行不同尺寸的网格加密设置，网格数分别为64.9 万、44.9 万和32.4 万。以P点为不同网格数计算的参考点，得到该点膛内压力-时间对比曲线，见图3。可见，与采用64.9 万网格数计算压力相比，使用44.9 万网格数进行计算时压力的相对误差约为2.3%，采用32.4 万网格数计算时压力的相对误差达到8.2%。综合考虑计算效率和计算精度，最终采用44.9 万网格数进行仿真计算，即膛口流场区域网格尺寸为0.5 mm × 0.5 mm，弹丸运动轨迹区域网格尺寸为0.25 mm × 0.25 mm，网格划分见图4。

图3 网格无关性验证Fig. 3 Grid independence verification

图4 网格划分示意图Fig. 4 Diagram of meshing

2.3 边界条件

枪管底部采用Fixed Support 固定，膛口流场水域外边界设置Flow Out 边界，模拟无限水域环境。药室为发射药的燃烧区域，通过设置起爆点模拟底火引燃发射药的过程，弹丸和身管中水介质受压由发射药燃烧输出得到。对弹丸运动设置压力阈值，当压力大于30 MPa 时弹丸开始运动。枪弹耦合存在间隙，身管内液体与外界水域相通，初始参数采用水深1 m 处的环境参数，即初始压力为101 325 Pa，初始温度为300 K。

3 计算结果与分析

针对枪弹耦合无间隙与间隙值为0.1 mm 的两种情况，设置装药量为25 g，进行仿真分析，发现两种情况的内弹道过程存在明显区别。根据组分分布图（图5（a））可以发现，水下枪枪弹耦合无间隙发射的整个内弹道过程均是弹体推动水柱运动，未发现有气幕生成；而设置0.1 mm 间隙后，在内弹道过程中出现膛内气幕（见图5（b）），2.5 ms 时气幕到达枪口，起到了提前排出弹前水柱的作用。

图5 2.5 ms 时刻内弹道组分分布Fig. 5 Internal ballistic component distribution at 2.5 ms

通过仿真还得到了内弹道过程中膛压与弹丸速度的变化规律。由图6（a）可知，当枪弹耦合间隙值为零时，整个内弹道过程耗时5.65 ms，膛内压力在2.1 ms 时达到最大，为368 MPa，是间隙值为0.1 mm 情况下最大膛压（271 MPa）的1.35 倍。当射弹在膛内运动时，若与水接触，就会受到水动压力阻力的影响，该阻力与水的密度、射弹速度的平方和接触面积成正比，因此当射弹速度越大时，弹体受动压力阻力也越大，这也是全水下射弹初速不高的重要原因。观察图6（b）可发现，在4.15 ms 时弹丸受到水产生的动压力阻力超过了膛内压力，射弹速度开始下降，出枪口时速度下降为347 m/s，仅为间隙值为0.1 mm 时弹丸炮口速度的43.7%。对比有、无间隙两种情况的速度变化可以发现，有间隙情况下射弹在1.2 ms 后加速度明显大于无间隙情况，原因是此时弹前气幕基本形成，射弹受水动压力阻力逐渐消失。根据仿真数据可以分析得出，水下枪枪弹耦合带间隙发射能够明显提高射弹初速，降低膛内压力，能够对水下枪全水下发射起到一定增益作用。

图6 无间隙与间隙0.1 mm 两种情况的内弹道参数变化曲线Fig. 6 Variation curves of internal ballistic parameters of the launching with no gap and 0.1 mm gap

为验证在不同装药条件下，水下枪发射是否均能生成管内气幕，并探究装药量对水下枪发射内弹道过程的影响，分别对3 种装药情况（21、25 和30 g）进行了有限元仿真。

图7 给出了3 种装药量下经有限元仿真得到的内弹道膛压及弹丸速度随时间的变化曲线。可见，随着装药量的增加，膛内压力明显增高，装药量为30 g 时最大膛压为421.3 MPa，是21 g 装药工况的2.26 倍；装药量分别为21、25、30 g 时，燃气射流分别在1.6、1.2 和0.8 ms 基本形成气幕，导致射弹加速度升高。生成的气幕分别在2.67、2.32 和1.85 ms 推动弹前水柱排出枪口，导致膛压变化曲线与弹丸速度曲线均出现拐点，其中随着装药量的增加，燃气射流泄出速度升高，单位时间泄出流量增加，导致拐点后的膛压下降速度明显提高，射弹速度的增长率略有下降。

图7 不同装药情况下内弹道参数变化曲线Fig. 7 Variation curves of internal ballistic parameters of the launching with different propellants

根据仿真结果，截取弹丸与燃气段组分分布情况，可以分析过间隙火药燃气射流在膛内的发展形成过程及压力、速度变化情况，图8～图10 分别为装药量为25 g 时膛内气液的组分分布、气液流速分布和压力云图。

图8 膛内气液组分分布Fig. 8 Distribution of gas and liquid components in the crucible

从图8 中气幕扩展过程可以看出，在25 g 装药的情况下，过间隙燃气在0.6 ms 时运动至弹丸顶部，由于Taylor 不稳定性作用，射流中心凹陷，出现分叉变形，部分射流贴壁运动。0.9 ms 时随着分叉现象进一步加剧，由于气液截面处速度高、压强低，射流出现卷吸回流现象，形成小型旋涡状湍流，射流头部两侧均有气核脱落。1.2 ms 时卷吸现象基本消失，射流呈现为贴壁射流，射流尚未汇聚成气幕。1.5 ms时射流长度达到1 倍弹丸长度，原来的两段贴壁射流逐渐汇聚，气幕基本形成。

图9 气液流速分布Fig. 9 Gas-liquid flow rate distribution

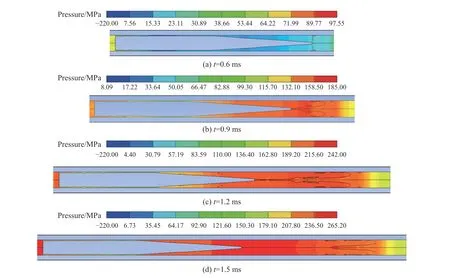
图10 压力云图Fig. 10 Pressure distribution

结合图9 可以看出：当t= 0.6 ms 时，过间隙火药燃气在膛内发展过程中，高速运动区域主要集中在枪弹耦合间隙区域，并且在出间隙过程中速度下降梯度较大，这是由于高速气体进入间隙时流通截面半径骤缩，气体流动速度增加，并在出间隙时流通截面扩增，同时运动受到液体阻滞，导致射流速度下降迅速；在t= 0.9 ms 时，射流产生的Taylor 空腔顶部出现回流，抑制了中心液体的轴向运动，出现中心低速区域；当t= 1.2 ms 时，随着燃气射流的轴向扩展，回流现象加剧，射流间低速区域轴向分布范围进一步增大；t= 1.5 ms 时，随着过间隙燃气射流的汇聚，中心低速区域的液体被逐渐排出，气幕流速逐渐增大。

图10 所示为燃气射流在膛内的压力演化过程。膛内燃气射流在发展过程中，高压区主要集中在燃气内部，通过图10 可以分析得出火药燃气过间隙时压力变化的普遍规律：在燃气进入间隙时，流速增加，导致压力有所降低；出间隙时燃气流通截面逐渐扩大，流速降低，燃气压力略有升高；当到达弹丸顶部时燃气迅速膨胀，在膛内液体中形成Taylor 空腔，压力沿程降低。观察燃气射流与液体交界面会发现，两相交汇处会出现局部高压区，这是由于射流Taylor 空腔顶端受到液体的阻挡，射流顶部产生压缩，从而出现局部高压。

4 实验研究

为了验证数值仿真的正确性，需要设计相关的实弹射击实验来对内弹道特征参数进行观测。

4.1 实验装置

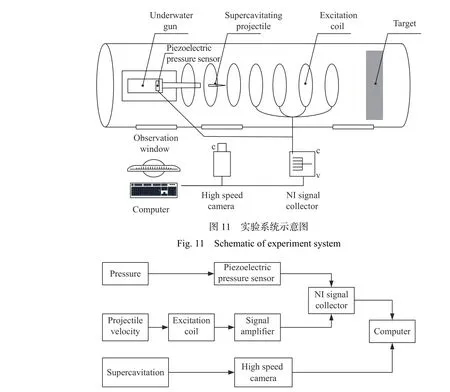
图12 测试系统框图Fig. 12 Diagram of testing system

实验系统如图11 和图12 所示，主要由水下枪发射装置、水下靶道、高速摄像机和水下综合测试系统4 部分组成，其中水下综合测试系统由膛压测试系统和水下射弹速度测试系统组成。水下枪发射装置安装在水下靶道的工作平台上，发射装置采用滑膛枪管，枪管与弹丸配合间隙为0.1 mm，当弹丸离开药室后，火药燃气可通过间隙与枪管中的液体相互作用。水下靶道内装满水介质，模拟全水下发射环境，测速线圈靶吊装于靶道中轴线上，安装间隔为1 m，靶道侧面设有观察窗，高速摄影设备通过观察窗拍摄膛口流场以及弹丸水下运动情况。

4.2 实验方法

在水下实弹射击实验中，采用对照实验方法，通过调整水下枪枪弹的配合间隙，验证间隙的有无对水下枪发射内弹道特性的影响；之后将间隙设置为0.1 mm，调整发射药的装药量分别为21、25、30 g，测试在枪弹耦合存在间隙的情况下发射药使用量对水下枪膛压及弹丸初速的影响。

速度测试原理如图13 所示，采用区截式测速工作原理[19]：在励磁线圈中加一恒定直流电流时，励磁线圈会产生恒定磁场，在铁磁性弹丸以速度v接近励磁线圈的过程中，会被励磁线圈磁场磁化，此时，根据电磁学原理，弹丸与感应线圈的关系可以用圆柱磁铁穿过感应线圈来等效。磁化弹丸切割感应线圈磁感线产生正弦电动势，输出至采集设备中。

基于此原理，弹丸在两个线圈靶之间的平均速度可以表示为

图13 线圈靶测速原理Fig. 13 Principle of magnetic velocity measurement

式中：Δl为两个线圈靶之间的距离，Δt为两个正弦信号过零点的时间差值。

本实验中，前两枚线圈靶分别安置于炮口前方0.5 m 和1.5 m 处。根据文献[20]弹丸在水下形成超空泡后，航行1 m 的速度降近似呈线性变化，因此该组线圈测得的平均速度可近似为炮口前1 m 处的弹丸速度。

根据牛顿第二定理

式中：m为射弹质量，A为射弹截面积，Cwx为等效阻力系数，vt为射弹余速。

对式（7）进行积分运算，并变换可得到

因此航程st为

式中：射弹质量m、截面积A、时间t、航程st以及射弹余速vt已知。联立式(8)和式(9)，可以求解射弹枪口速度v0和等效阻力系数Cwx。

4.3 实验结果

针对无间隙和间隙值为0.1 mm 的两种情况，采用25 g 装药分别进行了两次实验，得到了内弹道过程膛压曲线、测速系统测速情况以及弹丸出炮口后1 m 处超空泡形成情况。图14 显示了4 次实验的膛压变化。当间隙为0.1 mm 时，两次实验的膛压均降低到250 MPa 以下；而将间隙取消后，膛压分别升高了46.2%和62.2%。

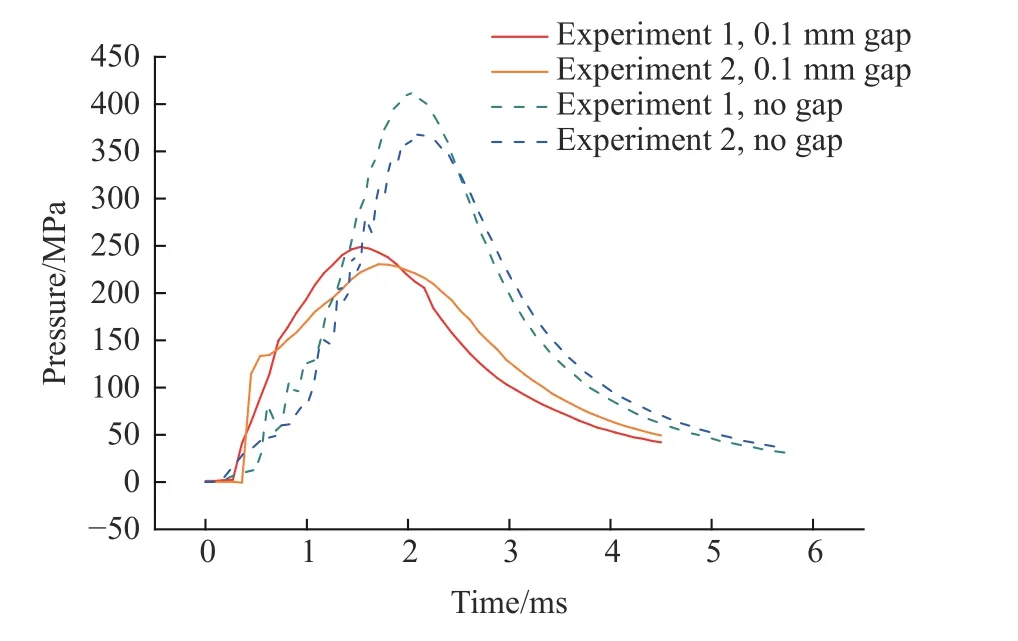
图14 有、无间隙两种情况下膛压的测试曲线Fig. 14 Pressure curve of the launching with no gap and 0.1 mm gap

根据图15 可知，当枪弹配合间隙为0.1 mm 时，弹丸出膛后，枪口前1 m 处的线圈靶测得两段正弦信号过零点的时刻分别为1 199.160 ms 和1 200.456 ms，计算得到该点弹丸存速还能达到771.6 m/s，形成的超空泡质量良好。而间隙去除后，膛口前1 m 处弹丸存速仅剩149.36 m/s。观察空泡形成情况可知，由于枪口速度不足，弹丸出膛后未能生成良好的空泡，运动轨迹产生了翻转，阻力急剧增大，导致弹丸解体，弹丸在水中的运动速度锐减。

图15 测速系统及高速摄影结果Fig. 15 Results of speed measuring system and high speed camera

由实验可知，当枪弹耦合设置0.1 mm 间隙后，内弹道过程中膛压下降明显，弹丸炮口速度显著提升，有利于产生稳定的超空泡包裹弹体，使其在水下运动时所受阻力大大降低，增加了射弹水下行程。

针对枪弹间隙为0.1 mm 的滑膛水下枪进行了3 种装药量的实弹射击实验，膛压测试系统记录了水下枪内弹道膛压随时间变化的曲线，如图16 所示。可以发现，随着装药量的减少，膛压峰值明显降低，弹丸膛内运动时间增长，分别在3.52、4.48 和5.15 ms 射出枪口。当装药量为25 g 时，根据实验时压电传感器测试位置，在仿真中设置探针，读取该处膛压的计算曲线，如图17 所示。将实验与仿真结果进行比较可以看出，膛压曲线的整体变化趋势相近，在2.3 ms 附近，两条膛压曲线均出现了较为明显的拐点，通过仿真可知该时刻燃气生成的气幕排出枪口，导致膛压的下降速度明显提高。实验的最大膛压出现于1.73 ms，仿真的最大膛压出现于1.89 ms，分别为247.8 MPa 和271.3 MPa，相对误差为2.01%。由此说明本研究采用的数值模型对水下枪发射内弹道过程的数值分析是准确的。

图16 不同装药量条件下膛压测试曲线Fig. 16 Pressure curve of different propellants

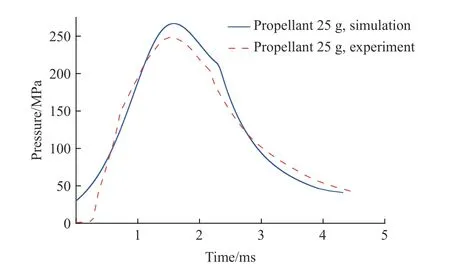
图17 膛压仿真测试对比曲线Fig. 17 Pressure comparison of simulation and experiment

实验记录水下枪发射内弹道特征参数如表3 所示。3 种装药情况下，炮口速度随着装药量的增加而增加；装药30 g 时，弹丸在炮口处速度达到896.7 m/s，两次实验速度均值相比21 g 装药提高了33.1%。与有限元仿真得到的数值相比，相对误差均在2.5%以内。根据仿真结果，在3 种装药情况下，水下枪发射时火药燃气均能利用枪弹配合的间隙产生弹前气幕，达到提前排水的目的，有效增加了射弹枪口初速。

表 3 水下射弹实验与数值计算结果Table 3 Experiment and numerical calculation results of underwater launch

5 结 论

以水下枪全水下带间隙发射方式的内弹道模型为基础，针对间隙对内弹道特性的影响以及不同装药量下带间隙发射是否均能生成弹前气幕等问题进行了研究。通过对内弹道过程中膛压、射弹速度和枪管内气液组分变化规律的分析以及实弹射击实验的对比验证，可得到以下结论。

（1）相对于水下枪枪弹配合无间隙发射，当枪弹耦合设置0.1 mm 间隙后，膛内气体和弹前水柱流动状态发生剧烈变化，由经典的弹推水柱变为气体先将水柱推出，从而卸载了大量弹前载荷，消除了液体对弹丸产生的动压力阻力影响，使弹丸炮口速度显著提升，内弹道过程中膛压下降明显，有利于产生稳定的超空泡包裹弹体，使其在水下运动时所受阻力大大降低，增加了射弹水下行程。

（2）在弹前气幕形成初期，由于Taylor 不稳定性作用，射流中心凹陷，出现分叉变形，随后出现卷吸回流现象，随着回流逐渐消失，燃气射流由贴壁射流汇聚成弹前气幕，将发射环境由液体变为低压气体环境。过间隙火药燃气在膛内发展过程中，高速运动区域主要集中在枪弹耦合间隙区域，高压区域主要集中在燃气内部，射流与液体交汇处会出现局部高压区。

（3）在3 种装药量情况下，内弹道过程均能产生弹前气幕，且随着装药量的增加，弹前气幕的形成时间与气幕排出炮口的时间均提前，膛内压力以及射弹枪口速度均明显增高。当装药量为30 g 时，最大膛压是21 g 装药的2.26 倍，射弹枪口速度提升约30%。3 种装药条件下，燃气射流生成的气幕排出枪口，导致膛压变化曲线与弹丸速度曲线均出现拐点，且随着装药量的增加，膛压下降速度明显提高，射弹速度增长率略有下降。

（4）枪弹配合间隙值对水下超空泡高速射弹武器内弹道特性有较为显著的影响，间隙值的优化对水下射弹发射技术的进步有至关重要的作用。