高温、高压、高应变速率动态过程晶体塑性有限元理论模型及其应用

刘静楠，叶常青，刘桂森，沈 耀

（上海交通大学材料科学与工程学院，上海 200240）

冲击载荷下的材料动力学响应、微观结构演化以及材料损伤与破坏一直是军事、材料科学及工程技术等领域关注的重点。动态冲击试验通常只能测定材料的初始微观结构、变形过程的力学响应以及变形后的宏观性能和部分微观结构，而无法直接测量冲击下材料微观结构的演化过程以及初始微观结构对材料宏观性能的影响过程。此外，动态冲击下被广泛使用的Bodner-Parton（BP）模型[1]、Johnson-Cook（JC）模型[2]、Zerilli-Armstrong（ZA）模型[3]以及Steinberg-Guinan（SG）[4]模型等宏观唯象材料本构模型并不包含塑性变形的微观机制，而只限于拟合实验数据，只在一定适用范围内描述实验中的应力-应变关系以及应变率效应，而无法描述冲击试验中的应力松弛[5]、弹性前驱波衰减[6]等异常现象。因此，考虑微观塑性滑移变形机制的动态晶体塑性模型在近年来得到了快速发展，并展现出对材料动力学响应与微观结构演化的描述能力。

材料在高压、高应变率下的宏观动力学特性和微观变形机理均与准静态下存在巨大的差异，适用于冲击加载的动态晶体塑性模型比准静态模型更为复杂，需考虑更多影响变形的宏观因素与微观机制。宏观因素包括影响变形的静水压强、温度等，微观机制包括声子拖曳、位错形核等位错行为，以及相变、孪生等变形模式。动态晶体塑性模型是在准静态模型的基础上建立的，继承了准静态模型的弹塑性变形框架，考虑了晶体中塑性滑移的各向异性，也可以考虑孪生与相变等变形机制，能够反映变形过程中的微观结构演化。但是，动态晶体塑性模型通常需要额外考虑材料的非线性弹性响应、大变形引起的显著温升效应以及位错在高速滑移下受到的声子阻碍[7]等因素，甚至在冲击载荷下材料可能发生的位错均匀形核[8-9]等机制。此外，材料在动态加载下相较于准静态加载更容易发生孪生[10-12]、相变[13-16]、断裂损伤[17-18]等变形机制。Roters 等[19]详述了准静态下晶体塑性模型的理论与应用。郑松林[20]也对晶体塑性模型在准静态与动态响应中的理论与应用进行了较为详细的介绍。本文侧重于动态冲击加载的晶体塑性模型，关于准静态的晶体塑性模型理论与应用可参阅Roters 等[19]和郑松林[20]的评论。

本文聚焦于动态冲击加载下的晶体塑性模型，详细综述动态晶体塑性有限元理论框架的运动学、弹性本构和塑性本构等组成部分，以及模型在孪生、相变、断裂损伤等不同变形机制中的扩展。动态晶体塑性理论模型框架的要点主要有冲击加载过程中温度的演化规律、热弹性耦合效应、状态方程在超弹性本构中的引入方法，以及声子拖曳效应对塑性滑移的阻碍作用等。高应变率冲击加载通常会引起材料内部的剧烈温升，因此动态晶体塑性模型在冲击加载下需要考虑温升带来的热弹性耦合效应。由于材料在冲击载荷下的体积变形很大，故通常采用高压状态方程(Equation of state，EOS)来描述材料的非线性弹性容变关系。对于高应变率下的塑性变形过程，材料晶格的声子振动会对位错的高速运动产生强烈的阻碍作用，即声子拖曳，且这种阻碍作用随着位错滑移速度的增加而强化，因此在动态冲击晶体塑性模型中必须引入声子拖曳机制来描述材料的应变率硬化过程。在动态冲击加载下，位错滑移往往不再是材料唯一的塑性变形方式，材料还可能通过相变、孪生、断裂损伤等变形方式释放体系的自由能。因此本文在基于位错滑移的动态晶体塑性模型框架之外还介绍了将相变、孪生、损伤等变形机制引入晶体塑性模型的方法，包括动态相变的驱动力与演化规律、孪晶的演化规律与硬化模型、层裂与绝热剪切带的形成及其对材料本构的影响。

1 变形运动学

在连续介质力学理论中，物质占据空间几何区域所构成的图形，称为物质构型。在变形或刚体运动过程中，物质构型将发生改变。为了对晶体材料的变形过程进行描述，需要建立晶体运动学框架。初始时刻未经变形的晶体材料占据的空间几何图形称为初始构型。采用拉格朗日坐标(X)来描述初始构型中任意物质点的位置。晶体材料在变形过程中的瞬时空间几何图形称为现时构型。对于初始构型中位于坐标X的物质点，在现时构型中采用欧拉坐标(x)描述其瞬时空间位置。显然，物质点在初始和现时构型之间具有x=x(X,t)的位置对应关系。描述材料变形程度的基本物理量通常选择变形梯度F= ∂x/∂X，其物理含义是现时构型相对于初始构型的梯度张量。物质点的运动速度通常定义在拉格朗日坐标系中v(X,t) = ∂x(X,t)/∂t，也可采用欧拉坐标表示为v(x,t) =v[X(x,t),t]，通常定义速度梯度L= ∂v/∂x描述物质点速度在现时构型中的梯度。

1.1 弹塑性变形分解

经典的运动学构型如图1 所示。晶体材料由初始构型经变形梯度(F)变换至现时构型，如图1中的黑色箭头所示。Hill 等[21]、Asaro 等[22]建立中间构型Ⅰ，将弹性和塑性变形进行乘和分解

图1 经典的晶体运动学构型Fig. 1 Classical configurations of crystal kinematics

式中：Fe、Fp分别为弹性和塑性变形梯度。材料由初始构型经塑性变形(Fp)变换至中间构型Ⅰ，再经弹性变形(Fe)变换至现时构型，如图1 中的红色箭头所示。弹性变形包括刚体旋转和晶格畸变，塑性变形可由位错滑移、相变、孪生等引起。将现时构型中速度梯度张量进行弹、塑性分解

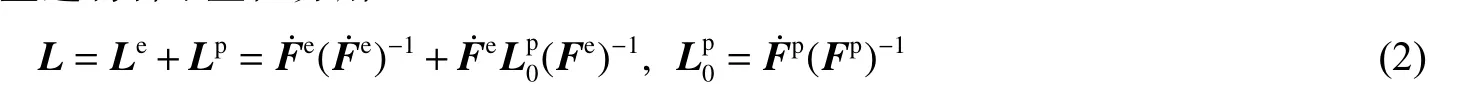
式中：Re为旋转张量，Ue为右伸长张量。材料由中间构型Ⅰ，经弹性拉伸(Ue)变换至中间构型Ⅱ，再经晶格旋转(Re)变换至现时构型，如图1 中的蓝色箭头所示。

图 2 引入热膨胀构型的变形梯度分解F = FeFθFp[19]Fig. 2 Decomposition of deformation gradient considered thermally-expanded configuration F=FeFθFp[19]

1.2 热膨胀构型

材料在动态冲击加载下往往存在显著的温升现象，而温升引起的热膨胀会导致材料内部应力、应变的变化，因此如何考虑热膨胀效应的影响是动态晶体塑性模型的一个重要问题。

在晶体塑性模型框架中，通常有两种考虑热膨胀效应的方法。第1 种方法是在弹塑性两构型的基础上额外引入热构型，将热变形与弹性变形解耦。第2 种方法不额外引入热构型，而在现有框架下基于热力学自由能进行推导，在求解超弹性本构过程中考虑热膨胀效应(详见2.2.2 节)。本节主要介绍第1 种引入热构型的方法。Clayton[23]、Vogler 等[24]、Hansen 等[25]、De 等[26]以及Shahba 等[27]在构型分解时加入了热构型Fθ，如图2 所示，将变形梯度分解为塑性变形、热变形以及弹性变形3 部分

式中：Fe、Fθ、Fp分别表示弹性变形梯度、热变形梯度和塑性变形梯度。

相应地，现时构型中的速度梯度可分解为

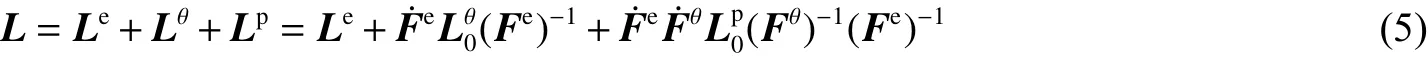
式中：Lθ、分别为现时构型和热构型中的热变形速度梯度，是温度变化率 (T˙)的函数

式中：α为热膨胀系数张量。

2 超弹性本构框架

通常在晶体塑性模型中有超弹性和次弹性两种描述材料弹性行为的本构关系。超弹性本构是指材料存在一个与应变相关的能量函数，其应力与应变全量之间的关系由能量函数决定，具有做功独立于加载路径的特点。次弹性本构描述应力率与应变率之间的关系，由于大变形下弹性模量是随应变全量变化的，其实际应用比较复杂，通常只用于小弹性变形情况[28](这种情况下弹性模量可视为常数)。考虑到实验中通常采用全量形式的高压固体状态方程描述材料的非线性容变关系，因此研究材料在冲击载荷下的大弹性变形行为时，往往采用超弹性本构来描述。

材料在冲击载荷下的超弹性本构关系主要包含基于热力学自由能的超弹性应力表达式以及考虑热弹性耦合效应的温升表达式两方面。其中，特别需要考虑热膨胀对应力的影响、弹性模量随压强和温度的变化，以及非线性弹性容变关系(固体状态方程)等。

2.1 超弹性本构的热力学框架

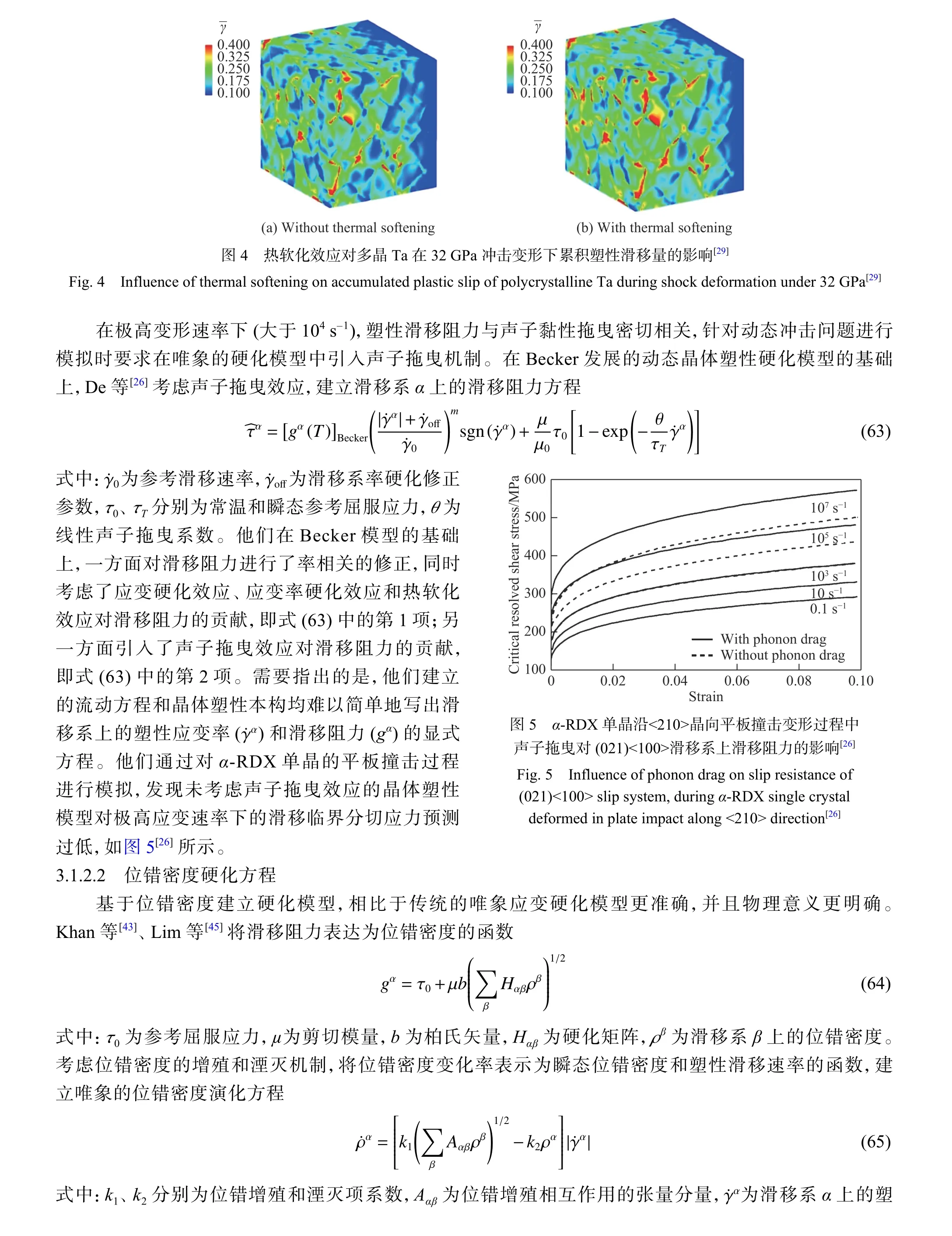
3.2 基于位错行为的动态晶体塑性框架

唯象的晶体塑性本构通常存在适用范围的局限性，只能在一定应变率区间内描述材料的塑性变形规律。因此为了满足不同应变率的加载条件，并同时描述各微观结构的演化，通常采用Orowan 方程作为流动法则的模型框架

Orowan 方程模型框架主要包含可动位错密度的演化以及平均位错速度与各内变量之间的关系两部分内容。可动位错密度演化部分需要考虑位错的形核、增殖、缠结、湮灭等微观过程。位错平均滑移速度部分可由位错滑移障碍物之间的平均距离除以在障碍物之间运动的平均时间得到。而位错在障碍物之间的平均运动时间可分成跨越障碍物的等待时间以及在障碍物之间的滑移时间两部分，位错的两个运动过程可分别由Arrhenius 热激活机制和黏性拖曳机制描述。

3.2.1 位错滑移速度

位错速度模型描述了位错滑移速度与滑移系分切应力以及位错滑移阻力之间的关系，主要可分为3 类：(1)简单指数模型，即基于实验中观察到的单根位错的运动规律，建立位错速度与分切应力的简单指数关系；(2)单一机制模型，即聚焦于位错在低应力区间内或高应力区间内的滑移规律，只采用单一的热激活模型或线性拖曳模型；(3)统一模型，即将位错的滑移过程分为跨越障碍物的等待过程以及在障碍物之间的滑移过程，统一了位错在不同应力区间内的滑移规律。

第1 类模型是基于单根位错实验结果的简单拟合，只描述了位错运动速度与应力之间的关系，不仅忽略了位错网络对滑移的阻碍作用，也没有考虑温度对滑移的影响。第2 类模型只描述位错在某一应力区间与温度范围内的单一规律，适用范围较窄，缺乏对位错完整滑移过程的描述。第3 类模型描述了位错滑移的整个物理过程，适用于不同的应力区间和温度范围。本节将简单介绍前两类模型，重点介绍适用范围最广的第3 类模型。

（1）简单指数模型

Johnston 与Gilman[62]利用蚀坑法测量了LiF 单晶中单根螺位错与刃位错在不同应力下的位错速度，根据位错运动速度与应力关系的实验结果得到以下结论：其一，刃位错的滑移速度比螺位错更快，但两者的差距在接近声速时逐渐消失；其二，位错运动的最高速度不能超过声速；其三，存在一个位错开始滑移的最低临界应力；其四，在低温低应力下，位错速度与温度近似满足负指数关系。这些结论已被证实在其他材料中同样适用。

基于上述实验结果，Gilman[63]提出了一种简单的位错速度与应力关系的指数模型

式中：D为特征阻力；v*为位错运动的极限速度，通常取材料的声速(剪切波速)。

上述简单的指数模型满足实验上位错速度的边界条件：当τ→0 时，v→0；当τ→∞时，v→v*。但该模型不仅缺乏对位错运动机制的解释，也没有反映出位错在低应力区间的转变特征。

为了将模型应用于更广的应力区间，Gilman[64]提出了在单指数模型的基础上添加一项在低应力区间内的位错速度

此外，Johnson 与Barker[65]相继提出了关于位错运动速度的指数模型，但这些模型均只是根据位错的运动趋势提出的唯象模型，缺乏相应的物理机制，且适用范围较窄。

（2）单一机制模型

单一机制模型包括只适用于低应力区间内的热激活机制以及只适用于高应力区间的线性拖曳机制。Alankar 等[66]、Zhang 等[67]、Monnet 等[68]采用热激活机制来描述位错在低应力区间内的滑移速度

式中：λ为障碍物之间的平均距离，vd为Debye 频率， ΔG0为参考激活能。此外，Hansen 等[25]、Nguyen 等[69]、Grilli 等[70]均采用线性拖曳模型来描述位错的滑移速度

式中：B为拖曳系数。

单一机制模型描述了位错在某一应力区间内的滑移规律，适用于模拟材料在特定加载区间内的变形过程。但实际上材料在不同时间或空间尺度上的应变率往往存在很大差距，单一机制模型难以描述这种复杂的变形过程。

（3）统一物理模型

目前使用最为广泛的模型基于Frost 与Ashby[71]首先提出的平均位错滑移速度模型框架。该框架将位错在障碍物之间的平均运动时间分成了跨越障碍物的等待时间以及在障碍物之间的滑移时间两部分，可分别采用热激活模型与声子拖曳模型来描述

式中：λα表示位错滑移过程中障碍物的平均距离，为热激活过程主导的位错脱钉所需要的等待时间，为声子拖曳主导的位错在障碍物之间黏性滑移所需要的时间。

对于滑移较为困难的体心立方(bcc)晶体材料，Shahba 等[27]、Lim 等[72]采用螺位错滑移的Kink-Pair 机制描述上述位错模型的两个滑移过程。Kink-Pair 滑移机制可分为两个阶段，如图6[27]所示。在第1 阶段，位错在障碍物(Peierls 能垒)前有一段等待时间，直到成功通过热激活方式跨越障碍物。在第2 阶段，位错分离成一对扭折并以黏性滑移的方式运动到下一个障碍物。对于面心立方(fcc)等晶体材料，也可根据与林位错的交互机制将位错滑移分为类似的等待过程与滑移过程两部分。

图6 螺位错滑移的Kink-pair 机制[27]Fig. 6 Illustration of screw dislocation motion via a Kink-pair mechanism[27]

式中：CT为缠结系数。

位错的湮灭指符号相反的位错在一定捕获距离内相遇所发生的消亡现象，决定了位错饱和密度的存在。Luscher 等[39]、Alankar 等[66]根据上述湮灭过程建立了简单的湮灭模型

式中：CA为湮灭系数，da为捕获距离。

为了分析冲击加载下位错各演化机制在不同压力下的主导地位转变，Lloyd 等[83]模拟了5～20 GPa加载下位错各个演化机制的占比情况，如图8[83]所示。在中低压(5～15 GPa)下，位错的增殖主要依赖于非均匀形核过程与增殖过程；当压力大到一定程度(大于20 GPa)时，材料发生剧烈的均匀形核过程，成为位错密度演化的主导因素。

实际上除了可动位错和不可动位错之外，位错密度还有许多其他区分方式。例如，Alankar 等[66,84]为了体现刃位错和螺位错滑移速率的差异，将位错密度分为螺位错ρs和刃位错ρe，并解释了基面取向的单晶Ti 的硬化率转变现象。此外，Keshavarz 等[85]、Liang 等[86]为了考虑几何必须位错引起的晶界效应，将位错区分为统计存储位错ρssd和几何必须位错ρGND，分析了在Al 双晶、Ni 基合金等材料中晶界对材料的硬化作用，并与实验结果较好地吻合。

图8 不同压力加载下位错密度的演化机制[83]Fig. 8 Dislocation density evolution mechanisms under different loading pressure[83]

4 动态相变

在高温、高压、高应变率动态冲击条件下，位错滑移往往不再是材料唯一的塑性变形方式，例如Fe、Ti 和RDX 等晶体材料也可通过相变与孪晶等方式实现变形。固体相变按原子的迁移方式可分为扩散型相变和位移型(切变)相变。而在高应变率动态变形下，材料发生的往往是切变型马氏体相变，整个相变过程无原子扩散，通过原子协同进行短距离迁移，并以切变的形式完成相变。本节重点介绍如何将马氏体相变机制引入晶体塑性有限元框架，以及在动态冲击与静态加载下相变驱动力与演化准则的差异。

当然除了在晶体塑性有限元框架中直接引入马氏体相变机制之外，也可采用相场与动态晶体塑性有限元结合的方法来模拟变形过程中的相变过程。不同于晶体塑性框架中的局部相变模型，相场法在自由能的基础上考虑了相变量在空间的分布及其所引起的梯度能。相场与动态晶体塑性模型相结合的方法已被广泛应用于模拟准静态下材料的相变、孪生与再结晶等变形过程[87-91]，该方法有望发展至模拟动态冲击下的相变、孪生等塑性变形过程。

4.1 马氏体相变运动学

关于马氏体相变介观模型的研究由来已久[92-96]。Thamburaja 和Anand[97]最初将马氏体相变机制引入晶体塑性框架中，以研究Ni-Ti 形状记忆合金的宏观力学响应，模型中总变形分为弹性变形和相变变形，忽略了位错滑移产生的塑性变形。在此基础上发展起来的更为广泛使用的模型考虑了塑性滑移，将变形梯度[13,98-99]分解为

式中：Fe、Fp、Ftr分别表示弹性变形、塑性变形以及相变对总变形梯度的贡献。

塑性变形包括母相与新相中的塑性滑移总和

式中：vp=1−vN表示母相的体积分数，

t=1为相变后新相的总体积分数，Nt为变体的数量，Nα和Nβ分别代表母相和新相的滑移系，和分别表示母相中的滑移方向和滑移面法向，和分别为新相中的滑移方向和滑移面法向。当相变产生的新相的位错滑移能力较弱时，往往只计及母相中的塑性滑移[100]。

马氏体相变过程的变形梯度为

式中：bt和mt分别为相变过程的切变向量和相变惯习面的法向。

4.2 相变驱动力与演化准则

相变模型的关键在于如何描述相变过程的驱动力以及相变的演化规律。本节将重点介绍在准静态和动态冲击下几种常用的相变驱动力与相变演化规律的模型。

4.2.1 相变驱动力

相变驱动力是与相变量功共轭的参量，取决于材料相变前后自由能的变化。在现有的研究中通常有两种方法描述相变驱动力与系统自由能的关系。第一种方法较为常见，直接将相变过程中Gibbs 自由能的变化作为相变的驱动力。第二种方法以Turteltaub 和Suiker[101-103]为代表，认为相变驱动力在Gibbs 自由能的变化之外还应额外加上一项相变熵增所导致的热驱动力，并指出这部分相变熵增并没有引起系统Gibbs 自由能的变化。上述两种方法在相变驱动力与Gibbs 自由能的关系表达式上存在区别，这一区别实际上来源于自由能定义的具体表达式和物理含义的不同，但是最终得到的相变驱动力是一致的，反映的物理规律是完全相同的。

相变驱动力与各热力学势函数之间的关系不完全相同[98]

式中：ft表示与相变量功共轭的相变驱动力，τm=FeTFeSFtr-T:表示相变过程的机械驱动力，ψ、G分别为系统的Helmholtz 自由能与Gibbs 自由能。

Manchiraju 等[104]为研究Ni-Ti 形状记忆合金中的相变过程，给出了系统的亥姆霍兹自由能表达式

式中：θ、θ0、θT分别表示瞬时温度、初始温度和相变温度，λT为单位体积的比热，htu表示不同相变变体之间的相容关系。式(88)中：第1 项表示弹性应变能；第2 项表示与热应变对应的自由能；第3 项表示相变过程中的化学能；第4 项表示马氏体变体之间的相互作用能，反映了变体之间的相互协调能力。

相变驱动力ft可根据式(87)中与亥姆霍兹自由能的关系得到

式中：S为PKⅡ应力。

此外，Feng 等[105]、Greeff 等[106]认为在冲击高温高压作用下，材料的相变驱动力主要依赖于系统的压强和温度。Cawkwell 等[38]根据材料在高压下的状态方程建立了一个评估两相Gibbs 自由能的模型，并给出了含能材料RDX 的α与γ相在不同温度与压强下的Gibbs 自由能之差，见图9[38]。该模型简化了相变驱动力的组成部分，忽略了两相的错配能以及相变的界面阻力等各个因素，通常只适用于材料的高压冲击相变过程。

4.2.2 相变演化规律

图9 RDX 的α 相与γ 相Gibbs 自由能之差与温度、压强的关系[38]Fig. 9 Difference between Gibbs free energies of the α and γ RDX polymorphs as a function of pressure and temperature[38]

相变过程中新相体积分数的演化依赖于相变的驱动力ft和相变的临界阻力fc。通常将相变过程中各种难以量化的阻力集合在一个总的相变临界阻力fc。因此，马氏体相变启动的临界条件为系统可提供的自由能达到马氏体相变的能垒

Turteltaub 等[101-102]、Tjahjanto 等[107]认为相变启动之后新相的生长速率依赖于驱动力与相变临界阻力的差值(ft-fc)，并依此提出了一个唯象的相变演化的动力学关系

式中：k为相变演化系数。

Thamburaja 等[97,108-110]、Manchiraju 等[104]则倾向于认为一旦相变驱动力ft超过临界阻力fc，马氏体相变过程会立即发生并释放系统的自由能，从而使相变驱动力永远满足自洽关系ft=fc，因此新相的生成 速率可根据相变的自洽关系求解

Barton 等[111]将上述唯象的相变演化动力学关系式(式(91))与固体状态方程相结合，模拟了Fe 在高压下的冲击相变 (α ↔ε)，如图10[111]所示。

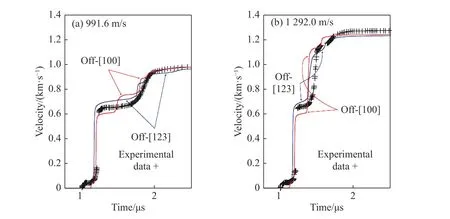
图10 Fe 冲击相变的单晶模拟与多晶实验结果[111]Fig. 10 Single crystal Fe simulation data and polycrystal experimental data of shock-induced phase transformation[111]

此外，考虑动态冲击过程中相变驱动力(Gibbs 自由能)依赖于压力和温度，Greeff 等[106]根据实验观察到的在一定压力区间内新相生长速率和压力满足指数关系，提出了适用于冲击高压下的相变演化模型

式中： ΔG(p)为两相的Gibbs 自由能之差，A、B是与相变演化相关的材料参数。

5 动态孪生变形

对于Ti[112-113]、Zr[10]等密排六方结构(hcp)材料，在冲击加载过程中，孪生变形与位错滑移是系统发生塑性变形和释放能量的主要途径，而相变往往需要更大的加载压力和应变速率[105]。孪生变形通常出现在滑移受阻引起的应力集中区域，通过均匀剪切的方式形成镜面对称的两部分晶体。由于孪生的应变速率敏感性通常低于位错滑移的应变速率敏感性[114]，即孪生阻力随应变率变化不大，材料在高应变率下比准静态下更倾向于发生孪生变形而非塑性滑移。因此，Cu[12]、Al[11,115]等滑移系较多的fcc 材料在高压冲击过程中也能观察到显著的孪生变形。

5.1 孪生运动学

Kalidindi[116]最先将孪生变形引入晶体塑性框架中，模拟了低层错能的多晶fcc 金属α-黄铜以及hcp 金属Zr 中的织构演化。Kalidindi 模型沿用了变形梯度的弹塑性分解

而塑性速度梯度包含材料的塑性滑移与孪生变形两部分

对于体积分数通常较小的fcc 和bcc 孪晶而言，往往只考虑母相中位错滑移而忽略孪晶内部的塑性滑移。但对于孪晶体积分数较大的情况如某些hcp 金属，孪晶中的位错滑移则不能忽略。因此，塑性变形梯度中应同时包含母相和孪晶中的位错滑移

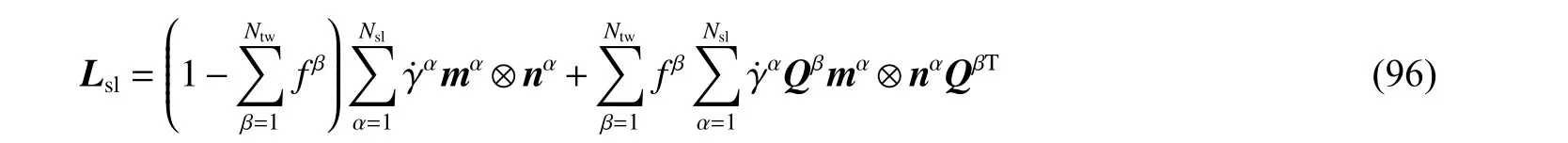
式中：fβ表示孪晶的体积分数，mα和nα分别表示柏氏矢量与滑移面法向，Qβ为孪生变形前后晶体位相的旋 转矩阵

绝热剪切带是材料在高速动态变形过程中由于局部温升过高引起热软化，在微观上发生剪切变形局域化的现象。由于变形时间极短，变形产热来不及扩散，剪切变形局域化几乎在绝热条件下进行。绝热剪切带表现为细长的窄带，其演变包括萌生、扩展和断裂3 个阶段。

材料在动态破坏过程中的微观结构动态演化缺少直接的测量结果，动态晶体塑性有限元方法对动态破坏力学响应和微观结构演化的预测及分析对于相关实验研究尤为重要。关于动态层裂破坏的模拟，主要介绍两种将损伤引入晶体塑性模型的方法；关于绝热剪切带的模拟，分别从忽略损伤和直接引入损伤两种思路对动态晶体塑性模拟方法进行具体介绍。

6.1 层 裂

层裂是材料动态破坏的一种特殊形式。受高速冲击加载时，材料内部两个卸载稀疏波相互作用，一旦材料中局部应力达到材料的动态强度极限即发生断裂，如图11[52]所示。因此，层裂是结构动态响应（波的交互作用）和材料动态响应（材料动态强度极限或破坏准则）共同作用的结果[51]。

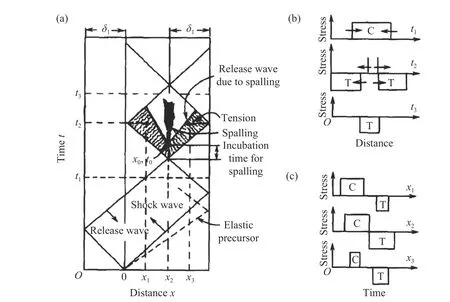
图11 冲击变形过程中波的传播及层裂现象(a)、3 个时刻的应力波形(b)和3 个位置的应力历史(c)[52]Fig. 11 Wave propagation and spalling phenomenon (a), stress profiles at three different times (b),as well as stress histories at three different positions (c) during shock deformation[52]

采用动态晶体塑性有限元对冲击层裂现象的研究主要有两种方法：（1）在动态晶体塑性模型中引入层裂破坏准则，通过显式地删除单元实现材料的损伤形核及其演化；（2）将材料视为有微孔洞的多孔晶体材料，在动态晶体塑性模型中基于孔洞体积在变形过程中的演化引入材料的损伤演化。下面具体介绍这两种动态冲击变形中层裂破坏的模拟方法。

6.1.1 考虑层裂破坏准则的晶体塑性模型

直接引入材料损伤是晶体塑性模拟动态层裂破坏的一个重要方法。依据损伤形核的难易程度，将晶体材料划分为不易损伤的晶内材料和易出现损伤形核点的结构(如晶界、第二相粒子处等)，对两者分别建立不同的材料模型进行研究。对晶内材料建立动态晶体塑性有限元模型，模拟动态冲击压缩过程中的晶内微观塑性变形行为；对晶体材料中易出现损伤形核点的结构，建立各向同性的宏观模型进行动态变形模拟，并结合层裂破坏准则对损伤形核进行定量预测。一旦模型中某个单元满足层裂破坏准则即成为损伤形核点，人为地将相应的单元抹去，即在模型中引入微孔洞。随着动态冲击变形的继续发生，微孔洞将会长大、合并。

材料失效模型通常有两类：内聚应力准则和损伤积累准则[129]。内聚应力准则假定材料失效是瞬态行为，当材料中的局部应力达到晶体的内聚应力即理论断裂强度时，材料立刻发生断裂。损伤积累准则假定材料失效依赖于变形历史，断裂的发生不仅与应力大小相关，还与应力持续时间相关。现有的动态层裂破坏晶体塑性有限元研究均简单地采用内聚应力准则，考虑到高应变速率变形中存在明显的断裂滞后现象，后续研究有待将损伤积累准则引入动态晶体塑性模型中。下面介绍两种典型的内聚应力准则：最大正拉应力准则和复合模式的最大应力准则。

最大正拉应力准则可表示为[130]

当材料所受正拉应力(σ)达到临界值(σc)时，则发生层裂破坏。Zhang 等[131]、Lloyd 等[132]分别以晶界和第二相粒子作为损伤形核点，采用该准则判断裂纹形核，通过动态晶体塑性有限元模拟冲击变形卸载过程中的层裂破坏现象。

复合模式的最大应力准则可表示为[23-24,57-58]

式中：s、τ分别为界面上的正应力和切应力，s0、τ0分别为参考正应力和参考切应力， ΔT为变形过程中的温升，s1、τ1分别为依赖于温升的临界正应力增量和临界切应力增量。当材料局部正应力或切应力超过对温度线性依赖的内禀界面强度时，均会引起材料的局部裂纹形核，随后由正应力和切应力主导的损伤演变略有不同。Clayton[23,57-58]、Vogler 等[24]将晶界视为损伤易形核点，采用该准则判断裂纹形核，模拟结果如图12(a)和图12(b)所示。样品右侧区域层裂开始形核，该区域材料承受着较大的拉伸应力，即层裂区域附近具有较大的弹性能。动态层裂破坏表现为晶间断裂，并且飞片的冲击加载速度越大，材料的层裂破坏越强烈，如图12(c)和图12(d)所示。

图12 铅合金动态晶体塑性有限元模拟结果：(a)层裂形核时的压力，(b)层裂形核时的弹性能密度，(c)经250 m/s 冲击加载层裂面附近的等效应力；(d)经350 m/s 冲击加载层裂面附近的等效应力[24]Fig. 12 Dynamic crystal plasticity finite element simulation results of lead alloy: (a) pressure of spalling nucleation;(b) elastic energy density of spalling nucleation; (c) equivalent stress near the spalling surface under 250 m/s shock loading; (d) equivalent stress near the spalling surface under 350 m/s shock loading[24]

6.1.2 基于孔洞体积演化的晶体塑性模型

图14 晶粒取向和应力三轴度对孔洞合并的临界状态变量的影响[133]Fig. 14 Influence of grain orientation and stress triaxiality on critical state variables for void coalescence[133]

6.2 绝热剪切带

绝热剪切带是材料在动态高应变速率加载变形过程中常发生的剪切变形局域化现象，最终会导致材料动态断裂[136-137]。Zener 和Hollomon[138]最早提出绝热剪切带的形成是热软化克服材料加工硬化的结果，并将微观绝热剪切带的形成与材料宏观热塑性软化(即变形后期应力-应变曲线发生下降)联系在一起，见图15[51]中Stage 3。绝热剪切带的基本特征包括：微观上观察到的绝热剪切带、宏观应力-应变曲线上发生热塑性失稳、高速变形过程接近绝热过程[51]。剪切局域化机理包含两方面竞争因素：促进形成剪切局域化的正面因素(即热软化和几何软化)和不利于剪切局域化的负面因素(即应变硬化和应变率硬化)[52]。

高速冲击变形过程中绝热剪切带的晶体塑性模拟研究主要有两种方法：（1）忽略损伤，直接模拟冲击变形过程中的塑性变形和温度演化，根据模拟结果在后处理中观测和分析绝热剪切带现象；（2）引入材料微观损伤，模拟动态冲击变形过程中绝热剪切带的形核及演化。下面分别对这两种方法进行具体介绍。

6.2.1 忽略损伤的晶体塑性模型

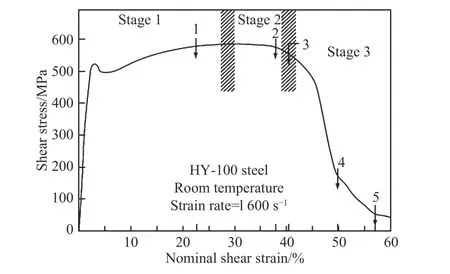
图15 经典应力-应变曲线上塑性变形的3 个阶段(Stage 1：均匀变形；Stage 2：非均匀变形；Stage 3：宏观热塑性失稳)[51]Fig. 15 Three stages of plastic deformation appeared on classical stress-strain curve (Stage1: homogeneous deformation; Stage2: inhomogeneous deformation;Stage3: macroscopic thermoplastic instability)[51]

高速变形下绝热剪切的动态晶体塑性有限元研究可以追溯到20 世纪90 年代，采用忽略损伤的动态晶体塑性有限元能够直接对高温、高压、高应变速率下绝热剪切带的形成及演变进行模拟。Hines 等[139]、Lee 等[140]基于单晶体弹塑性理论，忽略热效应，采用经典的应变率相关的唯象硬化本构方程，粗略地模拟了动态加载下的剪切带现象。Bronkhorst 等[141]、Tajalli 等[59]考虑塑性变形产热以及热软化效应，基于高速变形中的绝热假设进行热力耦合计算，采用唯象的动态晶体塑性有限元模拟分析绝热剪切局域化现象。考虑到动态变形温升显著并且对材料弹塑性本构具有重要影响[142]，Bargmann等[143]进一步考虑热弹性耦合效应和热传导效应，对动态变形温升进行更加精确的计算。他们同时考虑塑性产热、弹性产热以及热传导对温升的贡献，采用动态梯度晶体塑性有限元模拟104～107s−1应变速率范围的材料冲击变形行为。通过比较不同应变速率、相同变形程度的模拟结果，发现相比于高应变速率(107s−1)的动态变形，材料在相对较低应变速率(5×105s−1)下的动态变形过程中热传导效果明显，其温度梯度更为平缓，如图16 所示。

图16 不同累积滑移速率变形=0.05 时的温升云图[143]Fig. 16 Distribution of temperature increase when =0.05 for different accumulated slip rates[143]

采用上述动态晶体塑性有限元模型已经能够模拟绝热剪切带的形成，根据模拟得到的应力-应变曲线上热塑性失稳转折点的力学状态(如应变、应变率、剪切模量或变形能等)，进一步给出热塑性失稳等效判据，能够有效地对微观上可观察到的绝热剪切带形成的临界点进行预测和分析。当材料受到动态高速载荷时，虽然应力在屈服点附近可能存在短暂下降，但是宏观应力-应变曲线整体上首先经历一段上升，随后曲线发生持续性下降，如图15 所示。通常认为曲线上峰值转折点(即dσ/dε= 0 或dτ/dγ= 0)处宏观上开始发生热塑性失稳，同时意味着微观上开始形成绝热剪切带。发生宏观热塑性失稳时，除宏观应力之外，其他的变形或状态参量也会达到相应的临界值，相应地就有其他等效判据，共有4 种：临界应变判据[144-147]、临界应变率判据[148]、临界剪切模量判据[149-151]、临界变形能判据[152]。Zhang 等[147]通过动态晶体塑性有限元模拟得到的等效塑性应变云图上出现了绝热剪切带，如图17 所示。进一步采用临界应变判据能够预测宏观热塑性失稳临界点，即微观绝热剪切带形成的临界状态。他们根据模拟得到的宏观应力-应变曲线，对热塑性失稳转折点处的应变状态进行统计(见图18)，发现动态压缩过程中形成绝热剪切带的临界应变约4.5%，动态剪切过程中的临界应变约为3.7%。

图17 hcp 单晶和多晶样品在105 s-1 应变率下的绝热剪切局域化[147]Fig. 17 Adiabatic shear localization of hcp single crystal and polycrystalline samples under 105 s-1 strain rate[147]

6.2.2 引入损伤的晶体塑性模型

从微观角度考虑损伤的形核和演变机制是研究动态绝热剪切破坏的另一种重要方法。将损伤作为材料状态变量引入动态晶体塑性模型时，需要考虑3 个方面：引入损伤的弹性本构、损伤驱动力以及变形过程中损伤的演变。Boubaker 等[153]在超弹性本构方程中引入材料损伤，将弹性自由能视为弹性应变、温度和损伤变量的函数，将塑性自由能视为滑移速率和损伤变量的函数，将应力对损伤的依赖归因于弹性模量随损伤变量的变化，从而得到依赖于损伤的自由能和应力

图18 动态冲击载荷下6 种织构材料中形成绝热剪切带的临界应变(Vpeak = 20 m/s)[147]Fig. 18 Critical strain of adiabatic shear band nucleated in 6 different texture materials under dynamic shock loading (V peak=20 m/s) [147]

式中：ψ为比自由能，ψe、ψp分别为比自由能的弹性和塑性分量，S、Ee分别为PKⅡ应力和弹性格林-拉格朗日应变张量，T为瞬态温度，D为损伤变量，为滑移系α上的塑性滑移速率，ρ0为初始材料密度，C∗(T,D)为 依赖于温度和损伤的弹性模量， αΔT表示热膨胀应变。这里与式(116)相比增加了热膨胀构型，因此在应力表达式中采用了纯弹性应变，详见2.2.2 节。其次，热力学损伤驱动力可以通过自由能对损伤的依赖性得到

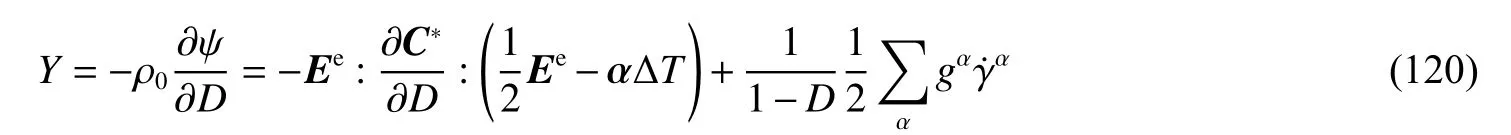
式中：Y为损伤驱动力，gα为滑移系α上的滑移阻力。显然，损伤驱动力和损伤变量是功共轭的。最后，损伤变量在动态变形过程中的演变可以通过损伤驱动力与损伤演化阻力比值的幂函数表示

式中：Yr为参考损伤演化阻力，Lp为速度梯度张量的塑性分量。在初始未变形条件下，损伤驱动力和损伤变量均为零；当材料受冲击载荷开始变形，则存在损伤驱动力，损伤变量不再为零，意味着材料发生损伤形核；在随后的变形过程中，损伤变量按式(121)随时间而变化，表示材料中损伤的演变规律。通过这样的方式，将连续介质损伤模型与晶体塑性模型进行耦合，能够有效地模拟动态绝热剪切破坏现象。

7 总结与展望

动态晶体塑性有限元对于研究高温、高压、高应变速率加载条件下的材料动态冲击力学响应和微观结构演化具有重要作用，但是如何对材料在动态冲击下微观变形的物理机制进行准确的描述仍然存在许多的发展空间。

在理论模型方面，动态晶体塑性有限元能够有效地反映晶体塑性滑移的各向异性、对微观组织的依赖性以及考虑动态冲击下各种影响变形的宏观因素与微观机制。与准静态晶体塑性模型相比，动态晶体塑性模型考虑了材料在高压下的非线性弹性响应、显著温升引起的热弹性耦合效应以及高速运动位错具有的声子拖曳效应等。但是目前对于冲击下位错高速滑移过程中位错之间的相互作用与位错形核、增殖的演化规律缺乏足够的认识，在未来的研究中可基于多尺度模拟框架，从分子动力学与位错动力学出发，探究位错在高速滑移的滑移特征和演化规律。

在应用研究方面，动态晶体塑性有限元能够应用于位错滑移、相变、孪晶和动态损伤破坏等变形与破坏机制研究中。现有的动态晶体塑性模型通过引入局部相变体积分数或孪晶体积分数及其演化规律，研究相变与孪晶对材料变形的影响，但这种方法只能均匀化地将相变与孪晶的影响简化为对材料点应力的影响，无法反映真实的相变过程与孪晶演化过程。在未来研究中可考虑将动态晶体塑性模型与相场模型相结合描述动态冲击下的相变和孪生过程。除了将动态晶体塑性模型应用于动态损伤破坏的定性研究，还可分别结合宏观破坏准则和微观损伤形核及演化准则，对动态冲击变形过程中的层裂和绝热剪切带进行定量预测和分析。从微观损伤演化的角度，对动态层裂和绝热剪切破坏的动态晶体塑性研究尚处于发展阶段，目前的损伤主要以引入损伤系数进行唯象的模拟为主，后续研究中需要更多地考虑基于物理的晶体动态损伤机制。

表 A1 运动学符号说明
Table A1 Symbol description of kinematics

Symbols Description F(Fe, Fp, Fθ ) Deformation gradient including elastic, plastic and thermal components L(Le, Lp, Lθ ) Velocity gradient including elastic, plastic and thermal components Re Rotation tensor Ue Right stretch tensor α Thermal expansion coefficient tensor

表 A2 热力学符号说明
Table A2 Symbol description of thermodynamics

Symbols Description Symbols Description Dint Intrinsic dissipation of the system K0 Bulk modulus at zero pressure ψ Helmholtz free energy K′ Pressure derivative of bulk modulus s Entropy of the system TD Debye temperature T Temperature R Molar gas constant KT Isothermal bulk modulus Mmol Molar mass of the material cV Heat capacity at constant volume kB Boltzmann constant Γ Grüneisen coefficient XTN Variables related to the lattice thermal vibration qn Internal variables for microscopic defects such as dislocations in materials XTE Variables related to the electron activation

表 A3 塑性本构符号说明
Table A3 Symbol description of plastic constitution

Symbols Description Symbols Description λ α Mean spacing between obstacles ρα for Forest dislocation density The drag-dominated mean transit time between obstacles Qα Activation energy B Viscous drag coefficient gα Slip resistance ˙ραnuc The nucleation rate gαath Athermal slip resistance ˙ραhom The homogeneous nucleation rate hαβ Hardening coefficient ˙ραhet The heterogeneous nucleation rate ρα Total dislocation density ˙ρα mult The multiplication rate ραm Mobile dislocation density ˙ραtrap The trapping rate τα Resolved shear stress tαr ρα i Immobile dislocation density ˙ραann The annihilation rate bα Burgers vector da Capture distance of annihilation vα Velocity of mobile dislocations tαw The thermal activation-dominated waiting time at a barrier ˙γα Slip rate on slip system α

表 A4 超弹性本构符号说明
Table A4 Symbol description of hyper-elastic constitution

Symbols Description Symbols Description I Second-order unit tensor ^Ee Isochoric strain in expanded configuration Ee Elastic Green-Lagrange strain^^Ee Isochoric strain in configuration I Ce Elastic right Cauchy-Green tensor Ee Volumetric strain in configuration I^Fe Isochoric part of elastic deformation S Second Piola-Kirchhoff stress Fe Volumetric expansion

表 A5 相变、孪晶与动态破坏符号说明
Table A5 Symbol description of phase transformation, twining and damage

Symbols Description Symbols Description Ftr Deformation gradient of phase transformation Sβ tw Twin resistance of twin system vp Volume fraction of the parent phase ρdeb Dislocationdebris density vt Volume fraction of the new phase t dmfp Dislocation mean free path related to the volume fraction of twin vN Volume fraction of all new phases φ Void volume fraction ft Driving force of phase transformation Fd Volumetricpartofplastic deformation gradient in porous crystal plastic model f β Volume fraction of twin Yr Resistance of damage evolution γtw Characteristic shear strain of twining