基于相对信任度贝叶斯的DEM 数据分析方法
2020-07-10徐红霞
徐红霞
(济源职业技术学院,河南 济源 459000)
数字高程模型DEM[1]包含了丰富的地理信息。不同分辨率的地形特征可以反映在DEM 中,因此大量的地表形态信息可以通过DEM 获取[2]。
近年来我国投入大量的资源来建设空间数据基础设施,国家地理信息系统得到不断发展和完善。其中构建的DEM 目前已经独立,可以为地学分析提供基础数据,在地理信息系统发挥重要作用。但在DEM 数据分类中没有考虑DEM 中地形属性如坡向、坡度等不确定分析受到对不同地形分类如丘陵,平原地区影响;没有考虑如坡度同一地形属性对于具体地形分类准确率的影响;对于地形分类,如果地形属性所占比例越多,地形分类将更加准确方便。地形分类的准确率与属性个数密切相关,通常个数越多准确率越高。但是分类的效率随着地形属性个数增多而降低[3]。
解决以上数据在分类时出现问题的方法主要有两种,一是贝叶斯(Bayes)分类算法,另一种是改进的几何超平面分类算法[4]。其中贝叶斯算法广泛应用于统计学中,比较容易实现。但是传统贝叶斯算法同时存在以下问题[5]。
传统贝叶斯算法应用过程时,首先需要先验概率的条件概率,将造成两大问题。第一是给出先验概率的条件概率本身比较困难。第二是不同专家给出的条件概率难以保持严格的一致性,需要检验概率的一致性。通常检验周期较长,将耗费大量的人力物力[6]。
传统贝叶斯算法组合证据过程中,对不同层次的证据无法进行识别和组合。因此需要构建统一的识别框架,否则如果强行组合不同层次数据时将导致结论失准。
传统贝叶斯方法存在的问题将导致在DEM 不确定分析和预测应用中存在一些问题。因此不能直接采用传统贝叶斯算法进行数据分类,应结合DEM 地形数据特点和传统贝叶斯算法存在的问题重新设计新的有效算法。因此提出一种基于相对信任度的贝叶斯算法用于DEM 地形分析。且利用该方法对DEM坡度、坡向、山脊线,山谷线地形因素进行数据分析,为地形研究和考察评价提供一种新的、可靠的预测分类方法。
1 算法思路
1.1 算法改进思路
传统的贝叶斯公式定义如下:假设存在一组两两不相容的事件A1,A2,…,An,且其中只有一个事件能和事件B同时发生,则存在如下关系:

其中,P(xj|Ci)是为类别Ci中分类属性Aj=xj的概率,其大小是根据训练集估计得出。
相对于决策树、SVM 等分类算法,贝叶斯算法理论上分类精度应该更高[7]。但是因为应用贝叶斯算法过程中,对不同属性的数据进行分类时,算法的作用不同[8]。部分数据的冗余属性将导致数据的维度提高,进而增加数据分类的计算量。同时还会产生噪声,降低分类的准确性。通过以上分析,为准确快速进行分类,采用特征选择算法对数据属性进行筛选。但是传统的特征选择方法在选择过程中,不同类别Ci(1 ≦i≦m)和数据的特征属性A的相关度最大值通常是关注焦点。但是不同特征属性A对分类的作用并不能只由该最大值来衡量,否则将导致分类结果不准确。分类过程中应该要考虑MI(Ai,Cj)的分布,即比较最大值与和其他各个类Cj(1 ≦j≦m,i≠j)相关性最大值两者的差距。如果前者相关度明显大于后者,才能说明其可以应用于分类过程。如果两者的相关度最大值差距不大,即使属性A与类别Ci(1 ≦i≦m)相关度最大值很大,这个特征属性也不能应用于数据分类[9]。
通过以上分析,提出一种基于互信息相对可信度的特征选择方法,相对可信度定义如下:

MI1 和MI2 分别是各个类与属性A间互信息的最大值和次大值,m和n分别是属性A的类别数和取值个数。MI1 与MI2 的差值反映属性A对分类的作用程度。其差值越大,对分类的作用越大,分类的可信度越高[10]。为将相对可信度定义成无量纲的值,分母部分采用MI2。
对传统贝叶斯算法进行改进,在贝叶斯算法中引入相对可信度R,并将其作为属性权值[11]。得到基于相对信任度贝叶斯算法为:

1.2 算法描述
基于相对信任度贝叶斯算法在对DEM 地形属性数据进行不确定分析和预测分类时候,具体算法流程[12-13]如下所述。
Stpe1:预处理原始DEM 地形属性数据,处理方法可采用离散化处理或者空值处理。
Stpe2:在训练坡度,坡向等DEM 属性数据样本时,用上述算法公式计算每个属性Ai分类的相对可信度Ri(1 ≤i≤N)。计算过程中,将相对可信度Ri从大到小排序,得到一组排列。并根据可信度大小选择部分属性形成新属性集合B,其中B={B1,B2,…,BK}。排列中前K个属性作为最佳属性被选入到新属性集合中来,后(N-K)个属性被删除。K是新属性集合中属性个数,由人为根据一定关系来确定。
Stpe3:计算每个类别在样本集合中出现的概率,采用不确定分析概率的计算公式为:

其中S和Si分别是样本容量和类别是Ci的属性个数。
Stpe4:计算stpe2 中新属性集合B 中每个属性BK 的条件概率,计算公式为:
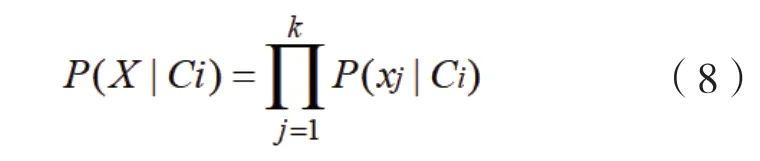
其中P(xj|Ci)为训练样本中类别Ci中属性Bj为xj的概率。
Stpe5:对DEM 地形进行分类,分类过程中权值采用基于互信息的相对可信度R,计算公式为:
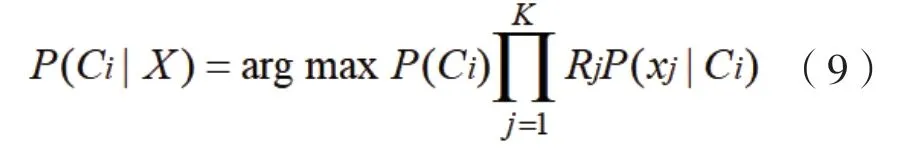
2 DEM 决策分析系统设计
DEM 决策分析业务系统分为四个主要模块。数据管理部分主要用于相关DEM 数据导入和手动建立数据模型。DEM 模型分析提取相关坡度,坡向等属性数据,同时利用贝叶斯等分析方法对提取的坡度,坡向等数据进行分析和预测分类。三维显示主要对模型和地形属性进行三维处理。统计输出模块主要对DEM 相关数据和属性进行统计查询和输出处理。DEM 决策分析业务流程图如下图1 所示。
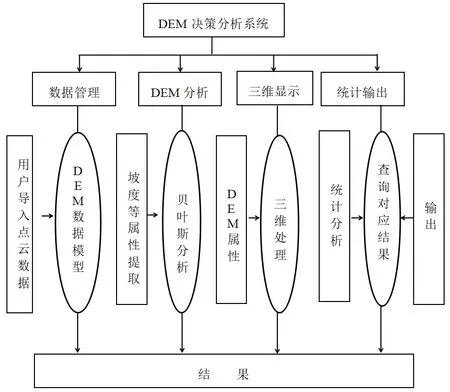
图1 DEM 决策分析业务流程图
3 实验分析
3.1 测试模型
针对改好后的基于相对信任度的贝叶斯算法在实际系统应用情况进行测试,在测试中对DEM 地形模型中的属性坡向,坡度以及山谷线,山脊线作为决策属性[14],对它们进行不确定分析,根据分析结果对地形进行分类测试,具体测试模型如下图2 所示。

图2 测试模型
3.2 时间性能测试
把改进的基于相对信任度的贝叶斯算法和传统贝叶斯算法进行在DEM 预测分析过程中的时间复杂度进行时间性能分析。为了方便两种算法的运行时间,用柱状图表示如下图3 所示。

图3 算法时间性能测试
3.3 准确率性能测试
评测DEM 地形分类准确率,是贝叶斯算法优劣的一个很重要的指标[15],其定义如下:

由特征选择方法选择得到部分属性,各属性作为决策属性的分类准确性结果根据准确率定义就可以算出。为直观比较传统贝叶斯算法和基于相对信任度的贝叶斯算法的分类的准确率,将两者用柱状图表示如下图4 所示。
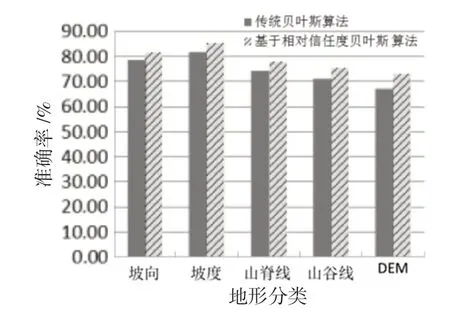
图4 准确率性能测试
3.4 测试结果分析
1)从图3 可以看出,改进后的基于相对信任度的贝叶斯算法和传统贝叶斯算法在DEM 地形分类、坡度、坡向以及其他DEM 属性进行分析过程中耗费时间都有所减少,效率得到了很大的提高。
2)从图4 可以看出,改进后的基于相对信任度的贝叶斯算法和传统贝叶斯算法在DEM 地形分类、坡度、坡向以及其他DEM 属性进行分析过程中准确率都有所提高。
4 结论
采用相对可信度R作为权值的改进的贝叶斯算法进行DEM 数据分析,可以有效提高坡度、坡向、山脊线、山谷线地形因素数据分析的准确率,减少运行时间,提高时间效率,为地形研究和考察评价提供了一种新的、可靠的预测分类方法。
