基于改进离散元强度折减法的堆积体边坡稳定性分析
2020-07-10侯明勋朱冬林
张 鹏,侯明勋,朱冬林
(1.上海交通大学船舶海洋与建筑工程学院,上海200240;2.中交第二公路勘察设计研究院有限公司,湖北武汉430052)
“十三五”期间,交通运输部在公路方面的投资达7.8万亿元[1],我国中西部地区的公路基础设施建设得到飞速发展。这些地区的工程地质条件复杂,广泛分布着松散堆积体边坡[2],穿越该区域的公路路堑边坡失稳问题频发,造成了巨大的经济损失和人员伤亡[3-4]。堆积体是指由第四纪复杂堆积作用形成的地质体,属于斜坡变形破坏后继续运动的产物[5]。一般认为堆积体为土石的混合体,物理性质介于土、石之间,完整性较差,非均匀性明显。丁秀丽等[6]通过室内实验发现,非饱和土石混合体在低围压下有明显的剪胀特性,且其变形模量与峰后强度随含石量增加而升高;王自高等[7]试验研究了梨园水电站大型堆积体天然状态下的剪应力-剪切位移特征,结果表明其抗剪强度较高;朱冬林等[8]从地质力学的角度分析堆积体边坡的变形稳定性;李安润等[9]通过有限元法和极限平衡法研究了降雨条件下转折型堆积体边坡的稳定性。离散单元法是在解决岩体不连续性工程问题的过程中逐步发展起来的一种数值计算方法[10],已广泛应用于岩土工程各领域。胡亚东[11]采用离散元软件(universal distinct element code,UDEC)研究了苗尾水电站右岸坝前堆积体变形破坏问题,揭示了堆积体边坡表层从剪切滑移发展至局部滑移-拉裂式的变形机制。
如前所述,学者们大多从地质力学角度或采用原始离散元强度折减法对堆积边坡进行综合评价,很少在离散单元法中考虑材料的摩擦角φ 和泊松比ν 对强度折减法评价边坡稳定性的影响。鉴于此,文中通过引入φ,ν 不等式改进离散元强度折减法[12],采用改进的离散元强度折减法计算不同开挖步下的堆积体安全系数,并对其稳定性进行评价。
1 离散元强度折减法的改进
1.1 基于摩擦角和泊松比不等式的离散元强度折减法
离散单元法的基本原理是将目标区域划分成块体单元,单元间的相互作用根据其接触关系和力与位移本构方程确定,各单元的运动状态由牛顿第二定律给出[13]。如图1所示,中心块体1在其他块体的5 组外力Fxi,Fyi(i=2,3,4,5,6)及其自身重力共同作用下,受到不平衡合力F及合力矩M的作用。块体1 的运动规律可依据牛顿第二定律F=ma 和刚体定轴转动定律M=Jβ 确定。
离散元中采用原始强度折减法计算边坡整体安全系数,评价边坡稳定性涉及的主要公式为:

图1 块体1上作用的外力集合Fig.1 Set of external forces acting on block 1

式中:c,φ 分别为材料原始黏聚力和摩擦角;ctrial,φtrial分别为折减后材料黏聚力和摩擦角;Ftrial为折减系数。
郑宏等[12]利用有限元强度折减法研究边坡稳定问题时发现,为能获得坡体合理的塑性区分布以及较准确的安全系数,对强度参数φ,ν 折减的同时,还需满足式(3),(4):

其中:E,ν 分别为材料原始的杨氏模量、泊松比;φi,Ei,νi分别为某一特定折减系数时材料的摩擦角、杨氏模量、泊松比。
1.2 算例验证
郑宏等[12]指出有限元强度折减法中c,φ 降低到一定程度时,往往模型边帮处塑性区尚未贯通而深部塑性区已贯通,这与工程实际情况不符。为验证在离散元强度折减法考虑φ,ν 不等式的正确性,文中以文献[12]中的均质边坡为模拟对象,分别采用原始离散元强度折减法和考虑φ,ν 不等式的离散元强度折减法对该坡体的塑性区及应变进行模拟分析。边坡模型如图2,均质土参数如表1,模拟软件为UDEC离散元软件。
图3为坡体安全系数为1.48时坡体塑性区及应变场的模拟计算结果。比较图3(a),(b)发现:两种方法计算的拉伸破坏区域几乎相同,原始离散元强度折减法计算的塑性区面积大且已贯通;考虑φ,ν 不等式的离散元强度折减法计算的塑性区域面积较小且分布相对分散,表明基于φ,ν 不等式的离散元强度折减法计算结果偏保守。比较图3(c),(d)可发现,两种方法计算出的应变较大区域皆为斜坡浅层,考虑φ,ν 不等式的离散元强度折减法计算的最大应变明显减小,但破坏模式一致。
综上可知,基于φ,ν 不等式的离散元强度折减法能准确判断坡体滑面位置且计算结果偏安全,有利于掌握边坡实际安全储备,节约不必要的工程支护成本。

表1 均质土材料参数Tab.1 Parameters of homogeneous soil materials
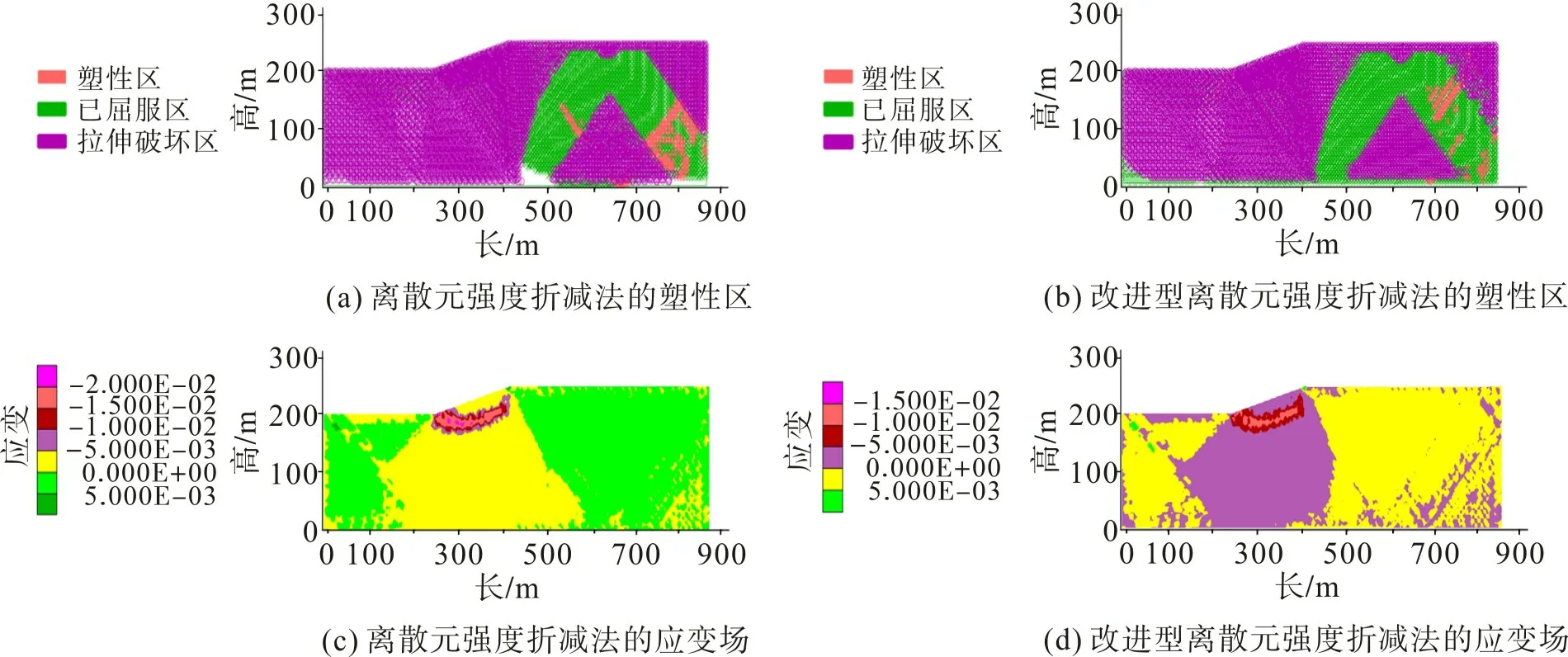
图3 两种方法下边坡应变场及塑性区分布Fig.3 Distribution of strain field and plastic zone of slope under two methods
2 堆积体边坡离散元模型的建立
2.1 工程地质概况
车峰坪堆积体边坡工程位于湖北省宜昌至保康段S223省道K10+120~K10+408,路堑区属构造剥蚀侵蚀中低山,呈不对称峡谷地形。图4为堆积体边坡典型断面简图及部分钻孔岩芯照片[8]。由图4(a)可看出,整体地形斜坡上边坡表面山沟与下边坡山脊相互交替形成“V”字型。根据现场勘察及工程地质综合分析发现:堆积体边坡地面高程在450~820 m之间,上下边坡间相对高差达370 m,该堆积体路堑边坡分5步开挖,每步边坡高8 m,开挖坡率为1∶1.5,平台宽2 m,上层4~5 m厚覆盖堆积体主要为碎石土夹黏土,由上至下呈逐渐松散状态;中腹部20~22 m深含小体量块石土;边坡中下部以碎石土为主,夹杂少量块石,厚36~50 m,下伏基岩为白云质灰岩。结合图4(b)可知,Ιc段高边坡土层多样,形状复杂,呈折线状,最具代表性。因此文中以Ιc段为例对车峰坪堆积体边坡的稳定性进行分析。
2.2 离散元边坡模型
根据车峰坪堆积体边坡工程Ιc段剖面地质概化简图,建立的UDEC计算模型如图5。模型长503 m,左侧高70 m,右侧高231 m,边坡表面以地表高程为基准并进行适当简化。图中1#,2#,3#,4#,5#点为选取的特征点。对模型左、右两侧边界及底部边界施加法向约束,边坡顶部为自由边界。

图4 堆积体边坡典型断面简图及部分钻孔岩芯照片Fig.4 Typical section diagram of accumulation body slope and some borehole core photo
2.3 岩土材料参数
根据现场工程勘察和室内测试确定岩土材料力学性质参数,结果如表2。UDEC 离散元计算所需的体积模量V、剪切模量G可由式(5),(6)确定:


图5 UDEC计算模型Fig.5 Computational model of UDEC

表2 堆积体边坡各岩土层力学性质参数Tab.2 Mechanical property parameters of each rock and soil layer of the accumulation body slope
3 堆积体边坡稳定性的模拟分析
以文中建立的堆积体边坡离散元模型为研究对象,利用UDEC软件,采用考虑φ,ν 不等式的强度折减法对其稳定性进行模拟分析。
3.1 堆积体边坡安全系数的计算
采用考虑φ,ν 不等式的强度折减法计算堆积体边坡在各步台阶开挖工况下的安全系数,结果如表3。由表3可知:边坡在自然状态下的安全系数为1.13,而现场勘察过程中,采用极限平衡法计算的堆积体边坡安全系数为1.15,两者计算结果极为接近;第3步台阶开挖后堆积体边坡安全系数≤0.98。依据《滑坡防治工程勘查规范》[14]中堆积体稳定性分级标准,该堆积体边坡在自然状态下处于基本稳定状态,第3步台阶开挖后边坡已处于欠稳定状态。

表3 边坡各开挖步的安全系数Tab.3 Safety coefficient of each excavation step of slope
3.2 堆积体边坡开挖变形的分析

图6 第1次开挖边坡位移矢量Fig.6 Vector of slope displacement of the first excavation
按照开挖设计,采用离散元软件UDEC 对边坡5 步开挖过程进行分析。图6 为堆积体第1 步开挖后的位移矢量。由图6可看出,第1步开挖后边坡总位移最大,为97.9 mm,且为竖向位移。其原因是初始边坡处于稳定状态后突然进行大面积卸载,土产生松弛效应导致竖向位移逐渐增大,堆积体上部的碎石土夹软黏土向下蠕动产生少量沿坡面向下的位移。
图7(a),(b)分别为堆积体边坡前4 步开挖后的塑性区及开挖卸载后的局部变形。从图7(a)可看出,第4步开挖完堆积体边坡出现了大范围的塑性破坏区,塑性区范围由堆积体上部延伸至开挖台阶处。由图7(b)可看出,5步开挖完台阶平台处出现明显的错位变形。
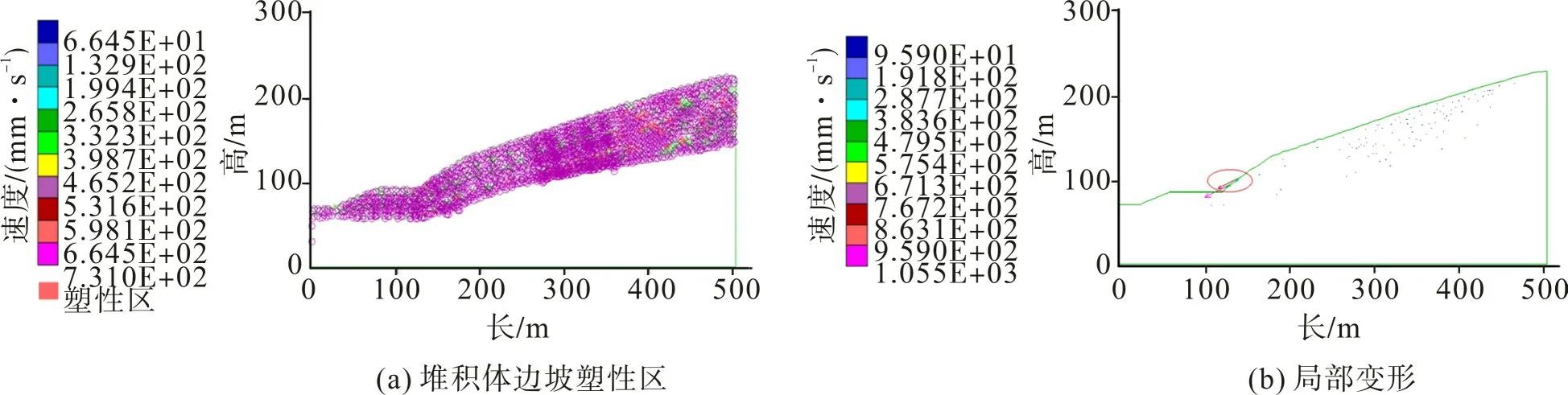
图7 堆积体边坡塑性区与局部变形Fig.7 Plastic zone of accumulation body slope and local deformation
图8为边坡Ιc区前缘斜坡陡峭区出现滑塌与局部错台现象的工程现场照片,与离散元软件UDEC显示的结果(图7(b))一致。

图8 边坡现场局部变形Fig.8 Local deformation of slope site
3.3 堆积体边坡特征点位移的分析
选取堆积体边坡各级平台的角点作为特征点,模拟研究开挖过程中堆积体边坡局部位移的变化规律。图9(a),(b)分别为特征点累计水平及竖向位移。由图9(a)可看出:各特征点的前3步开挖累积水平位移逐渐增大,后2步累积水平位移呈断崖式增长,且均为水平向左位移;前3步台阶特征点的累计水平位移值较大,第3步台阶特征点累计水平位移最大。这是由于上部堆积体逐渐失去下部的支撑力发生蠕变,导致表面覆盖层沿着边坡向下运动;第4,5步边坡开挖后产生的卸载效应导致中间第3步边坡受到上下的挤推力,致使3#点水平位移最大。由图9(b)可看出,每步特征点竖向位移皆有突变,以3#,4#,5#特征点最为明显,5#竖向位移最小。伴随着前4级台阶开挖完成,堆积体边坡蠕动减弱,其与土的松弛效应逐渐消散,故开挖至第5步台阶对特征点5#影响不大。
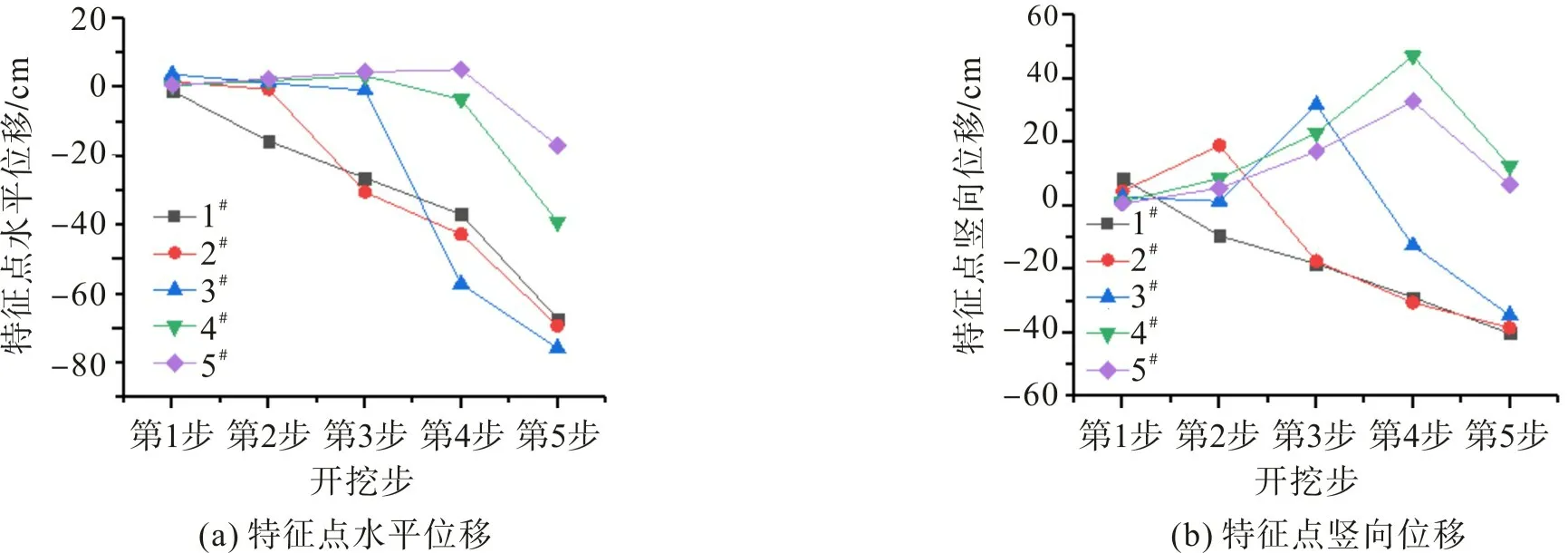
图9 特征点水平位移与竖向位移Fig.9 Horizontal and vertical displacement of feature points
上述模拟结果表明,堆积体边坡5级台阶开挖完,特征点1#,2#,3#的总位移较大,堆积体边坡处于不稳定状态,需对车峰坪堆积体边坡采取合理的加固措施。
4 加固后堆积体边坡稳定性的模拟分析
堆积体路堑边坡开挖后未得到及时防护是造成滑坡的主要因素之一[15]。冯玉涛等[16]采用抗滑挡墙并结合截、排水工程有效控制了高速公路堆积体路堑滑坡;何玉龙[17]针对隧道洞口堆积体,采用双层自进式锚杆大大降低了施工风险。上述模拟结果表明,车峰坪堆积体边坡处于不稳定状态,需制定相应支护方案。
1)针对堆积体边坡开挖后的蠕变效应,对表层软弱土进行处理,清理堆积体边坡表层部分碎石夹黏土,尽量减少蠕动荷载,降低施工风险。
2)针对前3步开挖完台阶边坡处于不稳定状态,每开挖完一级台阶,在坡面处设置全锚式锚索。锚索具体参数如表4,设置横向间距2.5 m,依据文献[18]设置长度25 m,最佳锚固角为30°,第1步开挖台阶锚索布置如图10。

表4 锚索参数Tab.4 Parameters of anchor cable
采用考虑φ,ν 不等式的强度折减法计算堆积体边坡各级台阶加固后的安全系数,结果如表5。由表5可看出,加固后边坡安全系数均逐步提高,参照文献[14],堆积体边坡各级台阶开挖后皆处于稳定状态,加固后第5步开挖边坡安全系数达1.61。
图11 为加固后堆积体边坡速度矢量。由图11可看出:加固后堆积体边坡最大速度矢量仅为9.57 mm·s-1,堆积体边坡下滑趋势减缓;加固后的台阶平台保持水平,表明局部滑塌、脱落得到有效控制。
图12 为加固后各特征点的累计位移。由图12可看出:采用锚索支护措施加固后,特征点的累计水平位移和竖向位移控制在10 cm 左右,但水平位移方向仍朝向左侧,竖向位移仍朝上;特征点的累计水平位移和竖向位移大大缩小,1#,2#,3#特征点位移量缩短小约90%,4#,5#特征点位移量减少约30%,锚索支护有效控制了堆积体边坡位移。

图10 第一级台阶锚索布置示意图Fig.10 Layout of anchor cable of the first step

表5 加固后边坡各开挖步的安全系数Tab.5 Safety coefficient of each excavation step of the slope after reinforcement

图11 加固后堆积体边坡速度矢量Fig.11 Velocity vector of accumulation body slope after reinforcement

图12 加固后特征点累计位移Fig.12 Cumulative displacement of monitoring points after reinforcement
5 结 论
1)相较于原始的离散元强度折减法,基于φ,ν 不等式的UDEC离散元强度折减法具有一定优越性,计算的安全系数偏保守,接近极限平衡法计算的结果,有利于掌握边坡实际安全储备。
2)堆积体边坡开挖引发的滑坡存在滑面滑塌、局部错位等潜在危险,需对其采取锚索支护措施,模拟结果表明,锚索支护加固后边坡安全系数逐步提高,减小了施工风险。
