粒子群优化算法
2020-07-10杨俊胜沈航驰代永强
杨俊胜,沈航驰,葛 鹏,代永强
(甘肃农业大学信息科学技术学院,甘肃 兰州 730070)
0 引言
粒子群算法是一种启发式进化计算技术,来源于 对简化社会群体智能行为模型的模拟,是由Kennedy和 Eberhart提出的一种进化计算方法,由于该算法具有搜索速度快,简单等一系列特点[1],已经成功应用于单目标优化问题,被认为是求解多目标优化问题最具潜力的方法之一[2],吸引了许多科研人员对该算法的优化,主要通过参数设置,与其他算法融合等方式进行研究,将算法不断的优化。
1 基本算法
pso算法是对生物种群觅食行为的仿真,算法描述了数量为 N的生物在空间中以不同的速度运动,每只鸟的飞行速度和运动方向[3],依赖于自身和生物群体的经验,在每一维空间中的速度和运动方向按下式调整:
粒子在多维空间中改变速度以及下一次运动方向的公式如下:
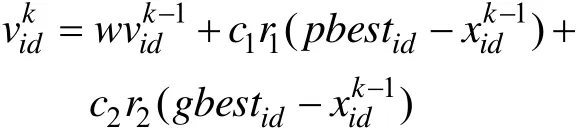
可以得到粒子i在第d维空间中的位置如下:

多维空间V中,粒子个数为N;
粒子i的位置为:Xi=Xiv(v=1,2,…,V),将粒子的位置作为参数带入标准测试函数,其结果作为相应的适应值;
粒子i速度变化为:Vi=Viv(v=1,2,…,V)
粒子i的历史最优位置:
Pbesti=Pbestiv(v=1,2,…,V)[5]
群体最优位置:Gbest=Gv(v=1,2,…,V)
2 算法实现流程
2.1 初始化
初始化算法的迭代次数,空间维度,以及种群数量和相应的测试函数参数的设置等等。
个体极值与全局最优解将粒子信息带入相应测试函数,个体最优为每个粒子找到的最优解,全局最优是从个体最优中通过比较获得再与历史全局最优比较,不断进行更新。
2.2 更新速度和位置
(1)速度更新公式
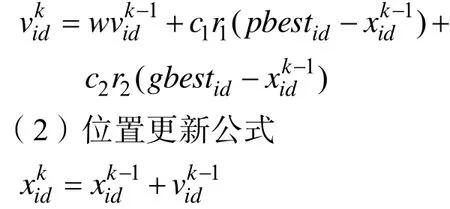
2.3 终止条件
(1)达到迭代次数
(2)满足全局最优位置满足最小界限[6]
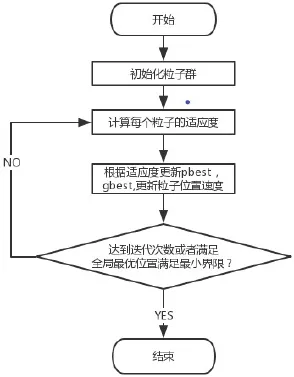
图1 算法流程图Fig.1 Algorithm flow chart
3 测试结果
3.1 测试函数

表1 测试函数Tab.1 Test functions
3.2 测试数据
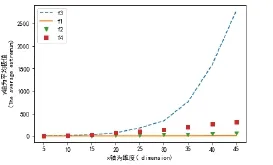
图2 维度对平均极值的影响Fig.2 The influence of dimension on average extremum

图3 种群数量对平均极值的影响Fig.3 The effect of population size on average extremum

图6 维度对标准差的影响Fig.6 The effect of dimension on standard deviation

图7 迭代次数对标准差的影响Fig.7 The influence of the number of iterationson the standard deviation

图8 种群数量对标准差的影响Fig.8 The influence of the number of iterations on the standard deviation
4 结论
由以上图示可以看出,通过控制维度,种群数量,迭代次数这三个参数中的任意两个,改变剩下的一个变量,发现维度,种群数量,迭代次数对四个测试函数的精度和稳定性有明显的影响。(图2,图(5),图(6)通过控制种群数量和迭代次数不变的方式,改变维度的值,发现测试函数的平均极值和标准差在 0-10之间稳定性较强,当维度大于 10之后平均极值和标准差增大,算法稳定性变差图(3),图(8)测试结果显示在种群数量在100之后,平均极值和标准差趋于稳定。图(4),图(7)得出当迭代次数在 100-200之间对平均极值和标准差的影响较为明显,200之后算法趋于稳定。在改变迭代次数,种群数量以及维度的值的同时,算法求解的解空间逐渐复杂,求解次数也在不断增加,导致求解问题的时间也在不断的变长。
5 结束语
粒子群算法(PSO)是人工智能算法之一,PSO算法在搜索高维度复杂解空间时相较于其他优化算法在速度上具有一定优势,收敛速度较快,但存在容易陷入局部最优的问题[7]。PSO算法在解决单层神经网络优化问题时,也具有较好的性能。但是在解空间维度极大的问题上(如优化 Inception v3网络)PSO的优化能力难以达到预期,因此对于这一类问题不建议直接使用PSO进行优化。将问题降维或拆分成简单子问题求解,可能是一种比较好的解决方案。建议将PSO算法与其他优化算法混用。总体来说PSO是一种很有潜力的优化算法。
