新高考体制下运用改进粒子群算法的排课算法

赵莹帝，孙光民，周青昱

（1. 北京工业大学 信息学部，北京 100124；2. 北京科技大学 自动化学院，北京 100091）

0 引言

学校的教育管理部门在整个教学过程中起着重要的作用，其中排课工作是最基础也是工作量最大的一项任务。随着高校不断扩招，各高校都面临教学资源紧张的问题。对于教务处来说，高效地做出一份合理的高质量的课表是困难的。所以根据实际教务工作实现计算机的智能优化排课势在必行。

排课问题已经被证明是 NP完全问题。最优化排课方案的本质即找到所有排课要素之间的对应关系，并寻找所有存在的对应关系的最优组合。排课问题面临的主要难点就是在教学资源紧张的情况下实现最优化配置。国内外很多学者[1-14]都对最优化排课问题进行了研究，并顺利解决原始排课问题。

有部分学者[1-4]使用模拟退火算法解决原始排课问题。有学者[1]提出改进的模拟退火排课算法，通过记忆当前最优解避免最优解遗失，并给出可变步长的温度更新函数。有学者[2]通过设定阈值判断收敛后的结果是否符合要求，如果不在规定范围内则认为进入局部最优，此时接受差解，并继续进行模拟退火过程寻找最优课表。也有学者[3]侧重对比大学和中学排课的不同，并分三个阶段进行模拟退火实现中学排课以减少算法运行时间。还有学者[4]基于局部状态计算，对临近代变化量求目标函数，减小计算量以解决排课问题。目前，还没有学者运用模拟退火算法解决新高考排课问题。

有部分学者[5-12]使用粒子群算法解决原始排课问题。有学者[5]级联粒子群算法和前行检测算法，比粒子群算法耗时长，但效果有改善。有学者[6-7]依靠权重进行新状态的选取，避免早熟收敛和局部最优解徘徊现象。也有学者[8]结合容易陷入局部最优但收敛速度快的粒子群算法和全局收敛性好但收敛速度慢的鱼群算法，得到具有较快局部搜索能力和较强全局收敛能力的混合优化算法，以解决原始排课问题。目前，还没有学者用粒子群算法解决新高考排课问题。

普遍教学资源紧张的中学排课问题有以下特点：第一，时间片较多，课表饱和易冲突。第二，课间短校园小，执行走班制课表较困难。第三，教室灵活性差，每个行政班一个教室，副科特殊教室数量少且专科专用。第四，某科中学教师每学期都只能教授该门课程，且不能同时教多个科目。在这种情况下实现最优化排课是有难度的，新高考体制下的最优化排课问题更具有挑战性。

新高考政策为“3+3”模式，即语数英加从“史地政物化生”六个科目中选取的三个科目。学校根据自身情况实施适合自己的特色走班制，目前走班制分为四种：不走班、小走班、大走班、全走班。考生可根据自身情况自由选取“史地政物化生”中的三个科目，不再受限于只能选文科或者理科。这样提高了学生选择的自由度，可以最大程度发挥学生的特点。学生选择自己擅长的三个科目参加高考以后，剩余的三科只需要通过会考即可。但同时带来的问题就是学校需要为他们开设不同选课模式的班级，并需要将“史地政物化生”的每科教师分成两组进行不同难易程度和不同教学计划备课，大幅度增加了学校教务处的排课任务量。

采用行政班制度进行排课有以下优点：第一，学生有固定教室，除副科外学生无需换教室上课，节约课间时间，减少课间换教室的迟到和安全问题。第二，有利于班级文化建设，也便于班主任管理。第三，每个班对应固定的教师，有利于教学计划同步推进。第四，预防换教室带来的私人物品被破坏等问题。

与原始排课不同，新高考体制下排课有更多约束条件。新高考体制下排课难点在于教学资源最优化分配。第一，“史地政物化生”的教师应分为两组，因为会考与高考要求不同，某教师不能教不同难度的相同科目，否则需要准备多份教案。第二，当六选三涉及的某教师课表发生冲突时，如果没有班级需要对应的该科目教师，该教师便处于课表非饱和状态，同时还需引入该科目的另外一名教师以解决冲突。故实现教师数最少的新高考体制下排课是有难度的。第三，约束条件的增加会给优化算法的初始解产生和优化效率带来挑战。

针对新高考政策下的排课问题，目前没有较成熟的实现方法。为了解决中学教学资源紧张的新高考体制下的排课问题，运用改进的模拟退火算法和改进的粒子群算法，将确定解作为优化算法的输入，用监督矩阵控制优化过程中课表始终满足硬约束条件和软约束条件，并使课表不断向用户自定义约束条件方向变化。分别使用改进的模拟退火算法和改进的粒子群算法实现新高考体制下的排课，并进行对比。最终，改进的粒子群排课算法可得到无冲突、教师数最少、教室数最少、教学计划同步推进的、符合新高考体制的最优化课表。

1 运用改进粒子群算法解决新高考排课问题

目前，粒子群算法被广泛应用于最优化问题。粒子群算法和模拟退火算法相似，从随机解出发，通过迭代寻找最优解，通过适应度评价解的质量。同时，粒子群算法是一种并行算法，寻优效率高。将确定解作为改进粒子群算法的输入，解决了新高考体制下排课问题和满足硬约束条件和软约束条件的随机初始课表难产生问题，并得到优化后的高质量课表。

改进的粒子群算法进行新高考体制下排课的算法流程如图1所示。

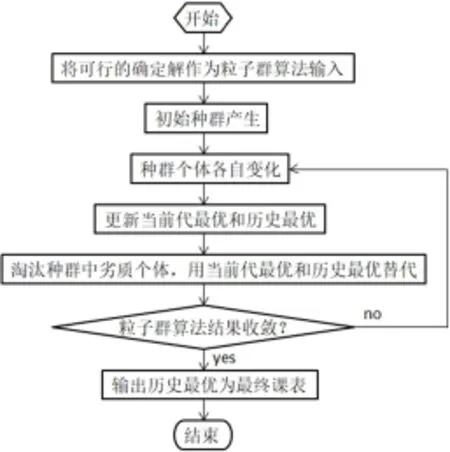
图1 改进粒子群算法进行新高考体制下排课流程图Fig.1 Flow chart of course arrangement under the new college entrance examination system by improved particle swarm optimization algorithm

解决排课问题需满足不同约束条件。设置硬约束条件为：第一，无两名教师同一时间进入同一班级授课。第二，无一名教师同一时间需要到两个班级授课。满足硬约束条件的课表才具有可行性。设置的软约束条件有三点：第一，满足教师总数最少。第二，满足教室数最少。第三，满足每天每科目最多一节课。满足软约束条件的课表具有实际应用价值。设置评分函数来衡量用户自定义约束条件的满足程度。课表评分越高，则越满足用户自定义约束条件。

最优化排课的本质就是寻找一组最优的排课要素分配方案，使课表一定满足硬约束条件和软约束条件的同时尽可能满足用户自定义约束条件。排课要素主要分为以下五点：时间、班级、教师、教室、课程。通过分析，简化了排课要素。每名中学教师只能教授一个科目，故课程信息等于教师信息。采用行政班进行新高考体制下的排课，除副科外每个班级学生都在本班教室上课，每个副科都有单独教室供所有班级错开时间段使用。将新高考体制下的排课要素简化为三个：班级、教师、时间。

针对简化后的排课要素，对课表信息进行编码，即考虑班级、教师和时间。时间片是确定且固定的，即每个班每周所需总课时数相同且不变。班级总数为不同选课模式班级数量的总和，需要根据学校实际情况进行计算。教师总数和不同科目教师数由不同选课模式班级数量决定。

时间和班级只包含单一信息可顺序编号，教师信息为复合信息需要同时包含科目号和该科目的教师号。采取的教师编码方式为：教师编号=科目号*group+教师组内号，其中科目号为所有科目顺序编号后确定的唯一编号，group为大于每个单科教师最大数量的确定值，教师组内号为教师在其所教授科目组中的具体编号。由于 group为预设定的值，当同时确定教师的科目号和教师组内号时，即可确定唯一的教师。对教师编号进行顺序编号，科目号可通过教师编号除以 group得到，教师组内号可通过教师编号对group取余得到。

大部分学者在处理原始排课问题时，采用二进制或十进制数串进行排课要素数据存储，不同字段表示不同排课要素。也有学者[16]使用矩阵进行排课要素的存储，这样更直观，也更便于约束条件的控制。学者刘腾[16]使用二维矩阵存储排课要素的对应关系，行和列分别为“时间”和“课程-教师-班级”，矩阵中存储“教室”信息。使用二维矩阵对课表信息进行存储。因为不同选课模式班级数量决定了班级总数和教师总数，同时时间片是预设定的。故将“时间”作为不同矩阵的列，将“班级”作为班级课表矩阵的行，将“教师”作为教师课表矩阵的行。班级课表矩阵中存放教师编号，教师课表矩阵中存放班级编号。因为班级课表矩阵和教师课表矩阵均包含某组课表的全部信息，所以它们在课表产生新解过程中可互为监督矩阵。

粒子群算法的输入一般为随机解，但满足教师数最少的新高考体制下的随机课表难产生。同时，在粒子群算法运行过程中去控制课表满足不同约束条件来获取最优课表是有风险的。将确定的初始课表作为改进粒子群算法的输入，干扰优化方向，尝试获取肯定满足硬约束条件和软约束条件的、较大程度满足用户自定义约束条件的、具有实际应用价值的最优课表。

规定每班每周的授课计划为：语数英各5节课，六选三选中的科目各4节课，六选三未选中的科目各2节课，自习课2节课，音乐、体育、美术、计算机、阅读这五个副科每科1节课。“3+3”涉及的教师可带2或3个班，六选三未选中的教师需带4个班。副科采取合班制，每名副科教师每周需上 5节课，即带10个班。自习课无教师，每班学生在自己班教室上课。

先为不同类型科目组设定固定的时间段，即设置满足每科目每天最多一节课的排课模板。在排课时，如果不同班级需要同一教师授课，在相同课时数的科目间顺序轮转以错开教师授课时间段。按课时数划分不同轮转组分别为：语数英、六选三选中的科目、六选三未选中的科目和自习、五个副科。在不同轮转组中，组内不同科目数大于等于组内单科教师所需最大带班数，不涉及模板增设问题。但副科采用合班制，五个副科轮转只有5种情况且由于教学资源紧张只设置一组副科特殊教室，故班级数量大于10时需要增加模板。为保证副科尽量被安排在下午，班级总数不宜大于40。六选三科目和自习的时间段固定，按科目时间片调整语数英和副科对应的时间段，可以分别设置不同模板。每十个班使用同一个模板，需要考虑模板交界处的冲突问题。当语数英教师带三个班时，可能会出现同一组教师跨模板排课情况。如果用W表示副科，X表示语文，Y表示数学，Z表示英语，每个科目对应课表中的五节课，则四组模板按顺序分别设置为：XYZW，WYZX，YWZX，ZXWY。在使用模板的基础上进行排课，顺序交换课时数相同的科目，即可满足教师数最少和教室数最少。

设置的评分函数仅用于测试改进的粒子群算法的课表寻优能力，也可以设置其他的评分函数。使用评分函数测试课表的用户自定义约束条件的满足程度，观察最终课表是否可以向预期方向变化。设定语数英每天从早到晚8个时间段的得分为8到1，副科和自习从早到晚不同时间段得分为1到8，“史地政物化生”科目不设置得分。当系统评分高时，语数英分布于早上，副科和自习分布于晚上，“史地政物化生”分布于一天的中间时段。遍历班级课表二维矩阵所有时间段，将得分求和后，将分数先除以班级数，除以159，再乘以100，即可得到归一化后的百分制评分。关于159的阐述：得分最高的情况为语数英分布于每天的前三节课，副科和自习分布于下午第4节课5个时间段以及下午第3节课2个时间段。故得分最高情况为159，并非22*8。

不同优化算法进行原始排课时迭代过程缓慢是因为在一次迭代中需要不断反复产生新解直至无冲突为止，这导致新解产生的效率低下。采用的新解产生机制是预设定交换次数为10，先随机到某个班级再交换该班级的某两节课，如果破坏硬约束条件和软约束条件则不交换。在交换过程中，要注意几点：第一，使用班级课表矩阵和教师课表矩阵互相监督，使课表恒满足硬约束条件和软约束条件成立。第二，设置副科教室监督矩阵，保证每科目每一时间段只有一名教师带班上课，从而保证教室数最少。第三，不改变“班级-教师”对应关系以保证教师数最少。第四，如果交换后某科目在同一天内出现两次，则取消交换。第五，自习没有教师，无需更新教师课表矩阵。第六，副科采用合班制，每次涉及副科交换应同时交换一组合班中另外一个班的对应位置两节课，并保证两个班的换课均不破坏硬约束条件和软约束条件。

每次新解产生后，需及时更新班级课表矩阵和教师课表矩阵。所采用的新解产生机制效率高，并且交换固定次数即保证新解一定可以快速产生。将交换次数设为适宜的值，可保证改进粒子群算法运行初期每一代均有新解产生，同时运行后期收敛速度适宜。

将30个相同的确定解作为初始种群，在种群更新过程中种群中每个个体各自历经一次新解产生机制，每一代新种群产生后对种群中每个个体进行单独评分，更新历史最优解和当前代最优解，淘汰每一代种群中评分最低的10个个体，其中5个用当前代最优解代替，另外5个用历史最优解代替。当历史最优解连续 1000代不发生变化则判定改进的粒子群算法终止。

2 实验结果和分析

针对北京市某高校的实际情况，对25个班级进行新高考体制下排课。其中“物化生”模式班级数量为6，“物生史”模式班级数量为5，“物化地”和“物生政”模式班级数量为 3，“物史政”和“史地政”模式班级数量为2，“物地政”、“化生地”、“生史政”、“化史政”模式班级数量均为1。“3+3”教师均带三个班级。几乎所有班级选课模式中都与物理有关，原因是考生所选三科中有物理才可申报较多数大学。

进行实验时，使用两种不同优化算法分别实现新高考体制下的排课并对比两种算法的优劣。在控制变量方面，两种优化算法使用相同的确定解作为优化算法输入、相同的新解产生机制、相同的评分函数以及相同的算法收敛条件。同时，设置最大算法运行代数为10000次。

进行实验后，两种改进优化算法的排课效果和排课速度各有特点，历史最优课表评分随算法运行代数变化对比如图2所示，收敛速度随算法运行代数变化对比如图3所示。

实验结果表明，所用改进的粒子群算法在新高考体制下排课可得到高质量的课表。相比于作为优化算法输入的确定解，两种优化算法均可提升课表的评分。改进粒子群算法具有较强的课表寻优能力，改进模拟退火算法运行时间较短。在实验过程中，改进模拟退火算法的参数很难调整，经常出现收敛速度过快或课表当前代评分始终震荡问题。

所用改进的粒子群算法的输出课表评分高于80，与确定解相比有明显提升。这说明最终输出课表在一定满足硬约束条件和软约束条件基础上，基本可完全满足用户自定义约束条件。改进粒子群算法输出的班级课表和教师课表部分结果分别如图 4和图5所示，其中六选三选中和未选中的相同科目分别用A、B来区分。

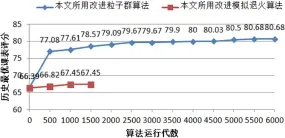
图2 当代最优课表评分随遗传代数变化折线图Fig.2 Broken line chart of contemporary optimal schedule score with the change of genetic algebra

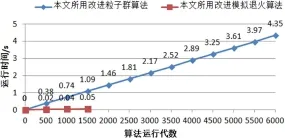
图3 收敛速度随遗传代数变化折线图Fig.3 The change of convergence rate with genetic algebra

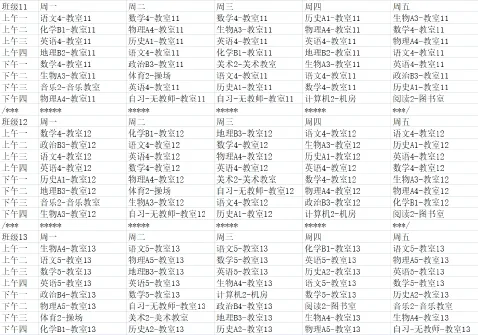
图4 改进粒子群算法排课的班级课表部分结果Fig.4 Some results of class schedule based on improved particle swarm optimization

图5 改进粒子群算法排课的教师课表部分结果Fig.5 Some results of teachers' timetable based on improved particle swarm optimization

3 结论

（1）文中所采用的改进粒子群算法拆分了变化更新的动态过程，将其拆分成淘汰机制和用历史最优解、当前代最优解替代种群中劣质个体，实现种群向理想方向运动，提高算法运行效率，减少算法运行时间。

（2）文中使用两种改进的优化算法解决新高考体制下的排课问题，并对比两种优化算法的特点。将确定解作为两种优化算法的输入，解决新高考体制下随机课表难生成的问题，同时深刻挖掘排课问题的不同要素大幅度减少排课时间。

（3）希望本文可以给其他解决新高考排课问题的学者带来参考意义，也可以给使用粒子群算法实现优化问题的学者带来新的改进思路。同时希望本文可以给解决受众广的新高考排课问题带来贡献，为解决其他NP完全问题和多约束时间调度问题提供帮助。