流形学习与成对约束联合正则化非负矩阵分解*

曹佳伟，钱鹏江

江南大学 数字媒体学院，江苏 无锡214122

1 引言

聚类是机器学习和数据挖掘领域中最基本的研究课题之一，它的目标是将数据点划分成不同的组份，并且相同组份中的样本之间具有很高的相似度。迄今为止，大量的聚类算法已经被提出，例如K均值聚类（K-means clustering）[1]、层次聚类（hierarchical clustering）[2-3]、谱聚类（spectral clustering）[4-5]、多视角聚类（multi-view clustering）[6-7]等。

最近，非负矩阵分解（nonnegative matrix factorization，NMF）[8]作为一种具有良好性能的松弛技术，其在聚类任务中已经得到了广泛的应用。现有的NMF算法大多是无监督的[9-15]，即它不使用数据标签或成对约束等监督信息。在许多实际问题中，很难获得数据集的全局监督信息，但局部监督信息相对容易获得，而有限的监督信息有助于提高机器学习算法的识别能力[16-18]。因此，将NMF扩展为一种半监督的算法将具有很大的实际应用价值。同时，利用流形学习方法来挖掘未标记数据中所蕴含的大量可用信息也是一种有效手段来提高算法模型的性能[13-15，18-19]。图正则化非负矩阵分解（graph regularized NMF，GNMF）[14]既考虑了原始实例空间中数据点的线性关系，也考虑了它们之间的非线性关系，因此它比普通的NMF具有更强的鉴别性。值得注意的是，标准的NMF 采用了相对于噪声和离群值不稳定的最小二乘误差函数，导致一些噪声特征或误差较大的离群值将主导目标函数。因此，需要一个更健壮的NMF 来解决噪声或异常值的问题。鲁棒的流形非负矩阵分解（robust manifold NMF，RMNMF）[15]使用了一种基于结构化稀疏范数的鲁棒公式，使其对数据中的噪声和离群值不敏感。

为了拓展关于半监督非负矩阵分解方法的研究，本文提出了一种流形学习与成对约束联合正则化非负矩阵分解聚类方法（nonnegative matrix factorizationbased clustering using joint regularization of manifold learning and pairwise constraints，NMF-JRMLPC），将成对约束引入到流形正则化框架中，从而能够高效地利用已知的监督信息；同时使用基于l2,1范数的损失函数来提升模型的鲁棒性。与Frobenius 范数相比，l2,1范数同时保持了每个数据向量的特征旋转不变性和最小化数据向量中的离群值影响，使得本文的目标函数比原始函数更为鲁棒。

2 相关工作

首先简单回顾一下非负矩阵分解[8]。给定一个输入数据矩阵X=[x1,x2,…,xn]∈ℜp×n，其中p是数据维度，n是样本数量。NMF 的目标是将矩阵X分解为两个非负矩阵F∈ℜp×k和G∈ℜn×k的乘积，使得它们的乘积是原始矩阵的一个很好的近似。为了得到两个非负的低秩矩阵，可以优化以下目标函数：

矩阵F的每一列可以被看作是一个位于新的表示空间中的基向量，而矩阵G中的每一行包含了一组F中列向量的线性组合系数。利用矩阵F的列向量与矩阵G的第i个行向量的线性组合来近似矩阵X的第i个列向量。实际上，矩阵G的第i个行向量是原始高维数据xi的低维表示，且新的表示空间的维度k远远小于原始空间的维度p。于是，高维向量就被低维坐标空间中的低维向量所表示。通过这个步骤可以去除原始数据中大量的冗余信息，从而提取出原始数据中的底层结构。与其他降维方法如主成分分析（principal component analysis，PCA）相比，NMF 分解后的矩阵因子不允许包含负值项，且只允许基向量在新的表示空间中的非负组合，这就是为什么NMF可以被视为一种基于部分的表示方法。

当使用NMF 进行聚类时，可以将k值设为数据的簇个数。具体来说，假设数据集由k个簇组成，则每个数据点可以属于这k个簇中的一个或多个。因此，NMF也可以看作是一种软聚类方法，即每个样本点的簇隶属度可以由G相应的行向量确定。更具体地说，检查G的每一行，如果k=，就将样本点xi分配给簇k。因此得到的矩阵G是数据的簇隶属度矩阵，从而也就得到了数据集的划分。

3 流形学习与成对约束联合正则化非负矩阵分解聚类方法

3.1 目标函数

给定数据矩阵X=[x1,x2,…,xn]∈ℜp×n，令G=[g1;g2;…;gn]∈ℜn×k是簇隶属度矩阵，其中n为样本个数，k为簇的个数。由于在许多现实问题中存在一小部分可用先验知识，例如样本之间的must-link 和cannot-link成对约束。于是，假设MS和CS分别表示必须关联集（must-link set）和不可能关联集（cannotlink set），它们来自给定的成对约束信息。用|∙|表示MS 或CS 中的条目数量。于是，结合流形学习方法与成对约束监督信息，得到如下目标函数：

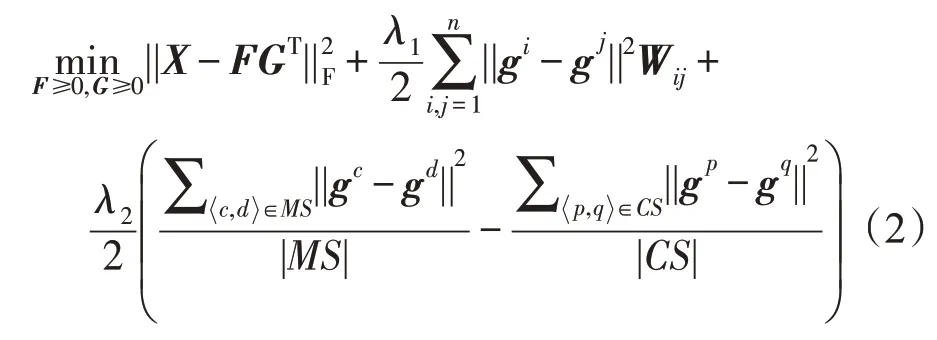
其中，边权值Wij表示样本之间的相似性；图拉普拉斯矩阵定义为L=D-W，D是对角度矩阵，且Dii=表示MS 中的任意条目，并且c、d是X中各自数据的索引值；同样的，表示CS中的任意条目，p和q是相应的数据索引值，c,d,p,q∈[1,n]。λ1和λ2是用来控制NMF 目标函数中三个部分比例的正则化系数。

事实上，任意两个样本xc和的类标签应该相同，因此xc和xd的理想的聚类结果分别为gc和gd中最大元素的索引值。于是，通过最小化||gc-gd||2得到这样一个条件。同样的，对于任意两个样本xp和的类标签应该不同，这就等价于最小化-||gp-gq||2，即。鉴于MS 和CS 之间的潜在数量级差距，这里采用了和的平均值。

显然，式（2）的形式不利于对问题的解决。这里定义一个矩阵Qn×n：

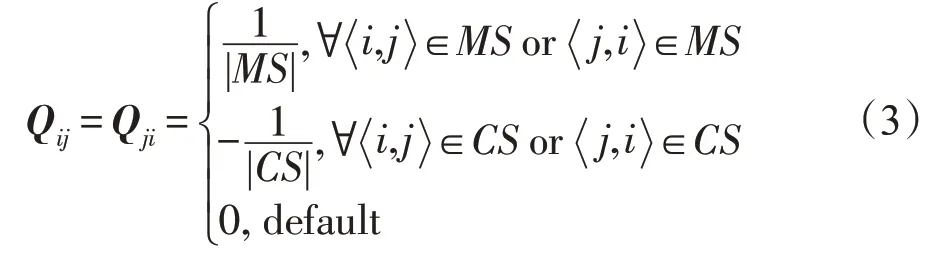
然后，根据谱聚类的思想[4]可以将目标函数简化为如下形式：

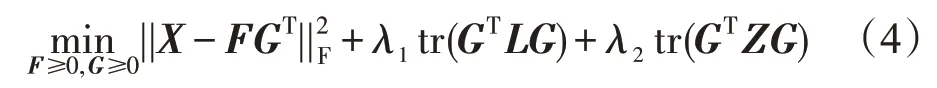
其中，Z=H-Q，Hii=∑jQij。并且，这里的Q、H和Z的角色分别类似于上述的W、D和L。

进一步将式（4）重写为如下：

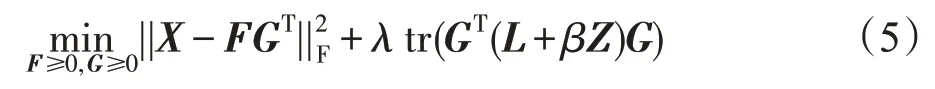
其中，λ=λ1且β=。

在式（5）中，参数β权衡了成对约束对图拉普拉斯的总体影响。但是，观察到参数β的数值范围常常难以估计，尤其是在tr(GTLG)和tr(GTZG)数量级不同时候。于是，需要如下定理来解决此问题。

定理1假设M是n×n维的对称矩阵，G是n×k维的嵌入矩阵，对于tr(GTMG)的范围先前是不确定的，通过使用转换M′=，可得0≤tr(GTM′G)≤1。其中λmin_M和λmax_M分别为M的最小和最大特征值，I为单位阵。

证明根据比例割（ratio cut）[4，20]、瑞利熵（Rayleigh quotient）[21-22]和极大极小值理论（min-max theorem）[23]可得如下不等式：

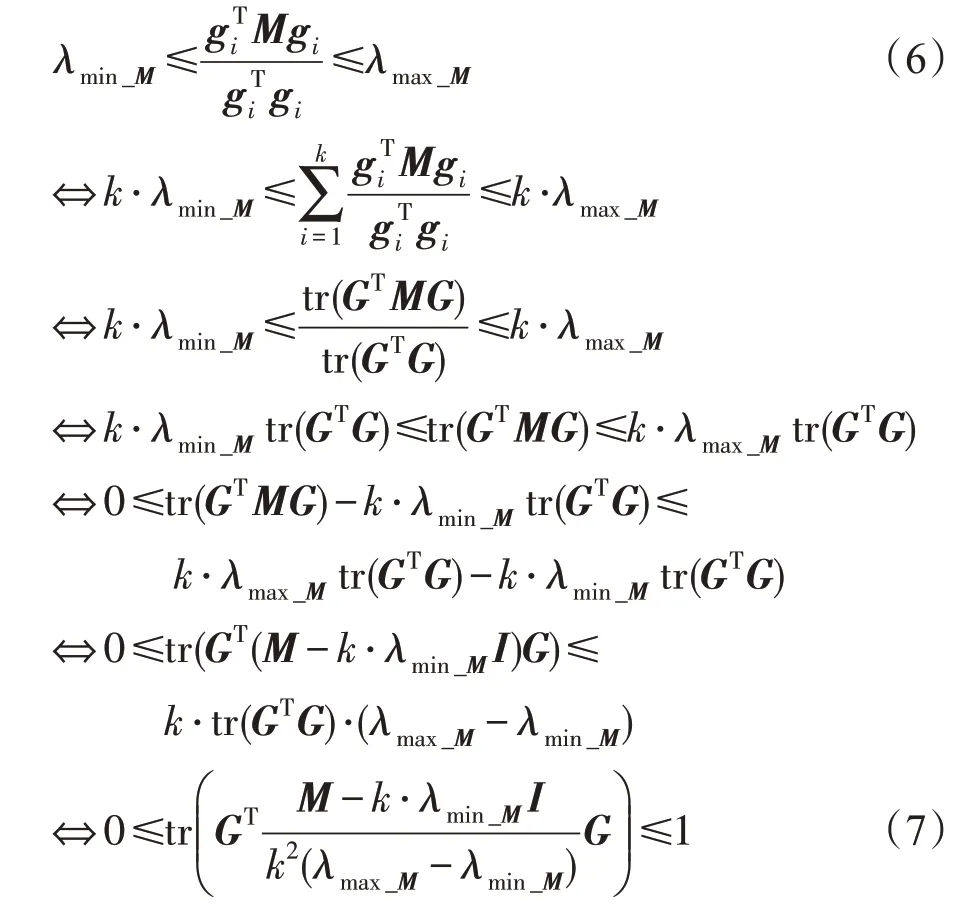
由此定理1得证。 □

因为L和Z都是对称的，基于上述理论有：

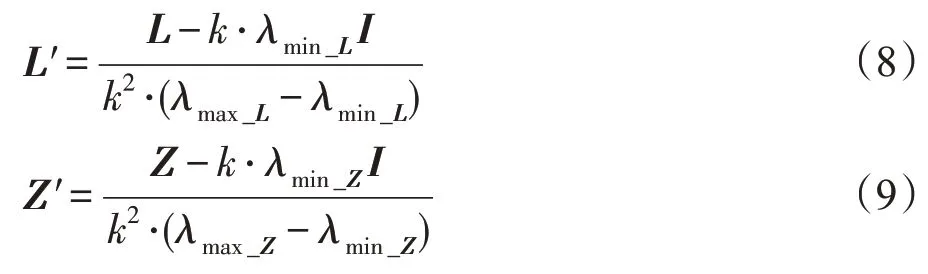
其中，λmin_L和λmax_L分别是L的最小和最大特征值，λmin_Z和λmax_Z分别是Z的最小和最大特征值，因此tr(GTL′G)和tr(GTZ′G)有相同的值域。

至此，就能够得到如下流形与成对约束联合正则化NMF框架：

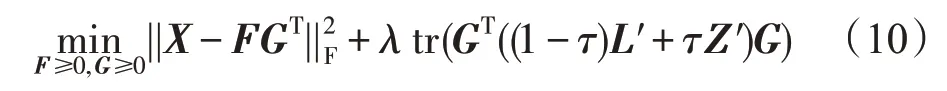
不同于tr(GTLG)与tr(GTZG)，tr(GTL′G)与tr(GTZ′G)的数量级是一致的。因此，使用一个简单的权衡系数τ∈[0,1)在任何数据场景中自适应地控制它们各自的影响。

最后，为了提升算法的鲁棒性，将损失函数中的Frobenius 范数替换为l2,1范数，就得到了NMFJRMLPC算法的目标函数：

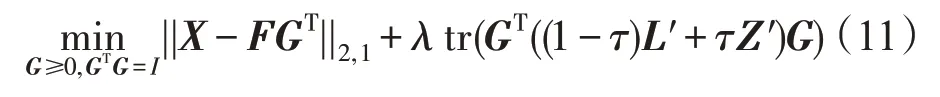
这里增加了一个额外的正交约束GTG=I，并且松弛了F的非负约束。其中，加入正交约束的主要目的有两个：第一个目的是为了保证解的唯一性。假设F*和G*是式（11）的解，那么对于任意给定的常数c＞1，无论F*和G*是局部最优解还是全局最优解，将cF*和G*/c代入目标函数中会使第一项中得到的值不变，而第二项中会得到较低的值。为了解决这个问题，文献[14]在算法收敛后通过标准化F的列来作为补救措施。因此，有必要通过引入正交约束来避免这样一个特别的步骤。第二个目的是降低算法的计算成本，稍后将对此进行详细说明。另外，松弛F的非负约束能够让算法处理具有混合符号的输入数据矩阵[15]。

3.2 算法优化

注意，上述目标函数中存在F和G两个变量。使用增广拉格朗日乘子法（augmented Lagrangian multiplier，ALM）来对本文的算法进行优化。在此，首先引入两个辅助变量E=X-FGT和H=G，并且令S=(1-τ)L′+τZ′。然后重写目标函数：

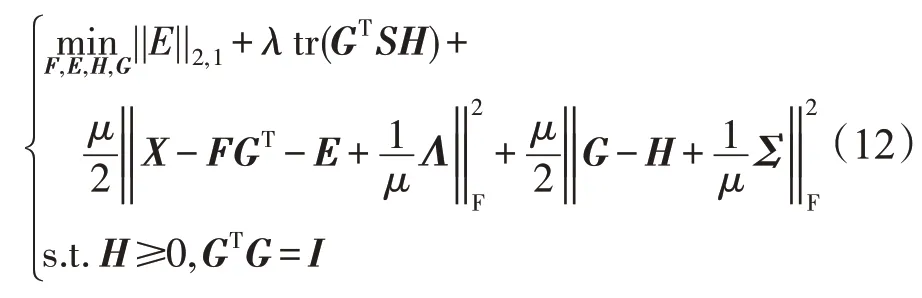
这里的μ、Λ和Σ都为ALM 框架中的参数；μ是决定不可行性惩罚的规范化系数；Λ和Σ都是用来惩罚目标变量和辅助变量之间的差距；并且μ是标量，Λ和Σ是两个n×k维的矩阵。下面通过迭代优化的方法来更新每一个变量。

（1）更新E

固定F、H和G，目标函数变为：

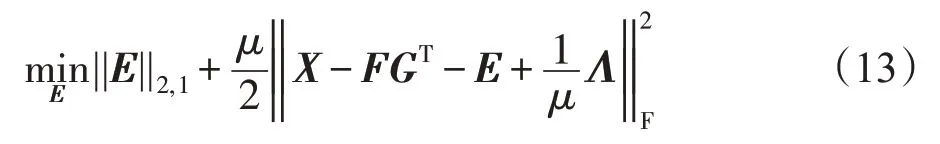
这里需要定理2来解决式（13），这个定理也在文献[24]中作为命题1 被提出。由于篇幅问题，不再对其进行详细的证明。

定理2给定一个矩阵W=[w1,w2,…,wn]∈ℜm×n和一个正标量λ，则X*是式（14）的最优解。

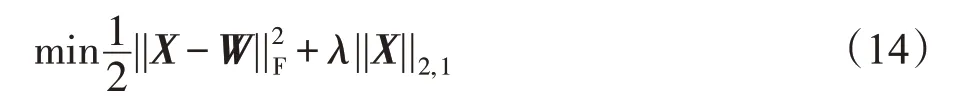
并且X*的第i列为：

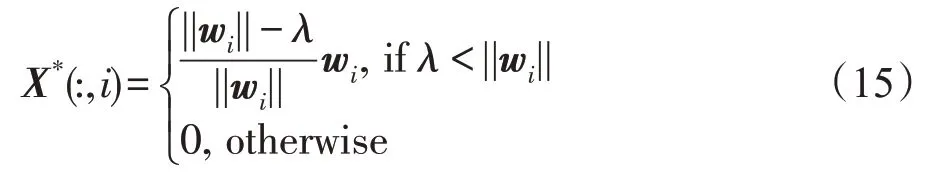
因此，式（13）可以写成如下形式：

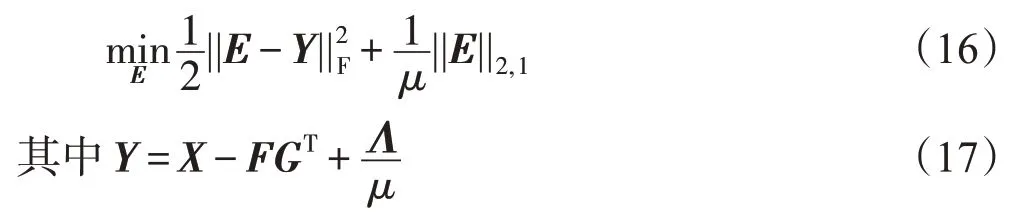
于是，根据定理2可以得到式（13）的解为：

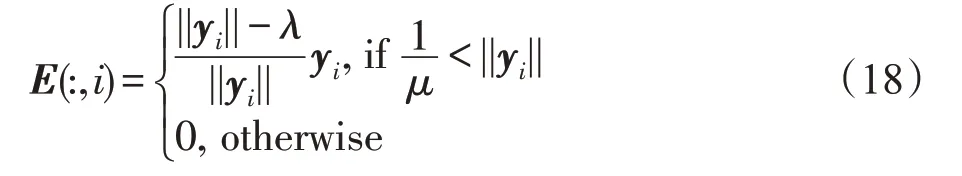
其中，yi是Y的列。

（2）更新F

固定E、H和G，目标函数变为：

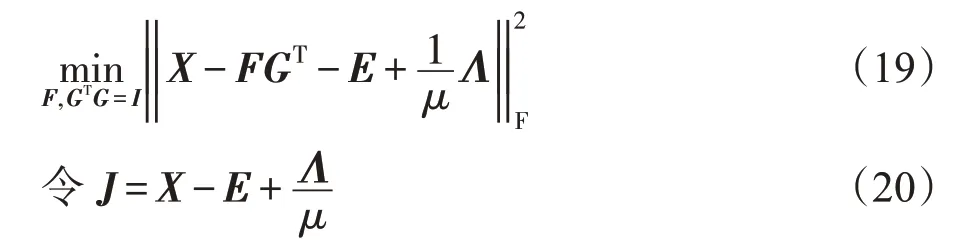
由于GTG=I，得到F的解为：

若不加入正交约束，则目标函数变为：

令上式关于F的一阶导数为0，则F的最优解可由下式得到：

于是，可以得到：

这就意味着除了保证解的唯一性外，有必要对G施加正交约束，否则求解F就需要对大尺寸矩阵进行求逆运算。显然，加入正交约束能够大大降低计算成本。这是加入正交约束的第二个目的。

（3）更新H

固定F、E和G，目标函数变为：

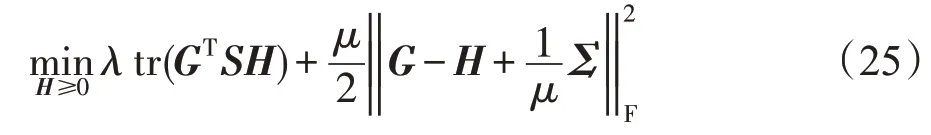
展开式（25）并舍弃与H无关的项得：

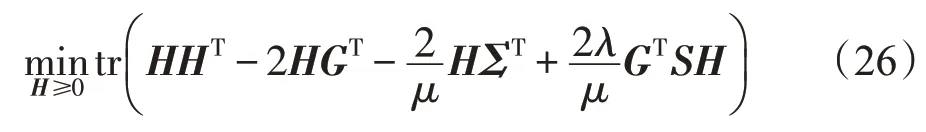
化简式（26）得：

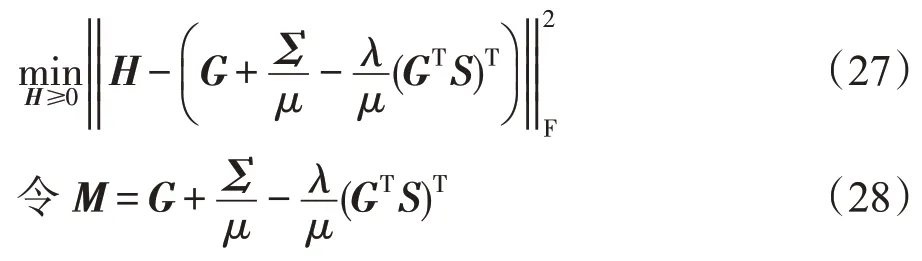
可得H的解为：

（4）更新G

固定F、E和H，目标函数变为：

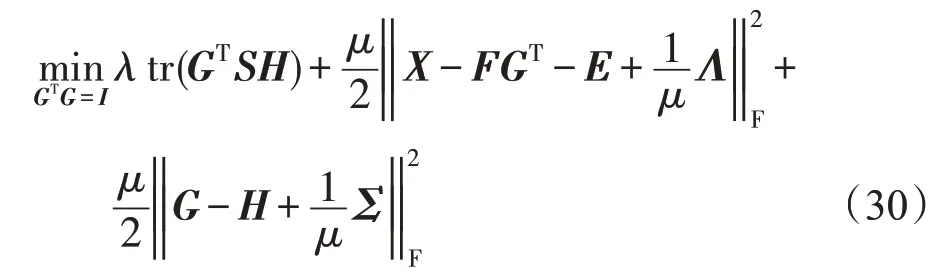
和上一部分优化H的过程相似，令：

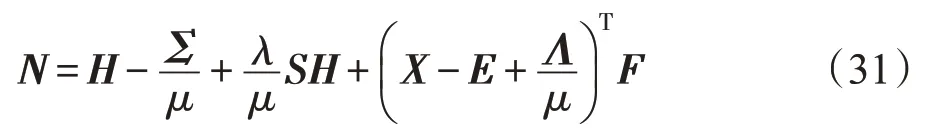
可将式（30）写为如下形式：

显然，式（32）等价于如下式子：

则G的最优解为：

其中，U和V是对N进行奇异值分解之后的左右奇异向量组成的矩阵。详细证明过程可见文献[25]中的理论1。

（5）更新μ、Σ和Λ

更新完F、E、H和G四个变量之后，还需要对ALM框架中的参数进行更新：

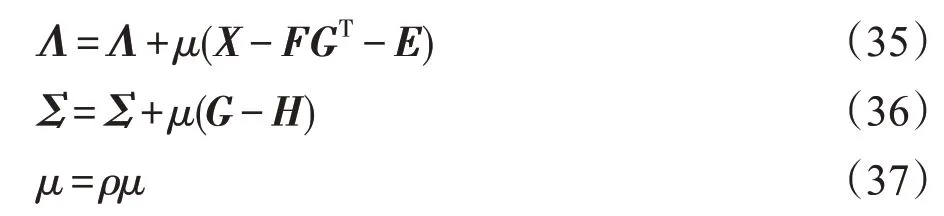
其中，ρ＞1是用来控制收敛速度的。ρ越大，收敛所需的迭代次数就越少，但与此同时会降低算法的精度。

NMF-JRMLPC算法步骤如下：

输入：数据矩阵X，类别数k、μ、λ、τ，部分有标记样本信息。

输出：簇隶属度矩阵G。

（1）初始化F和G，并根据式（8）和式（9）分别计算L′和Z′。

（2）根据式（17）和式（18）计算E。

（3）根据式（20）和式（21）计算F。

（4）根据式（28）和式（29）计算H。

（5）根据式（31）和式（34）计算G。

（6）根据式（35）、式（36）和式（37）分别计算Λ、Σ和μ。

重复步骤（2）至（5），直到算法收敛。

3.3 算法收敛性分析

在上一部分对本文方法进行了总结。注意到：随着迭代次数的增加，μ以指数级开始增长；同时，式（12）中的目标函数逐渐地收敛为式（11）中的原始目标函数。这是因为当μ变为无穷大时，为了保持目标函数值是有限的，则式（12）中的第三项和第四项必须为0。因此，只要给定充足的迭代次数，就能够保证本文算法的收敛性。并且，本文算法的收敛依赖于ALM 框架的收敛。在文献[26]中，已经证明和讨论了ALM框架的收敛性。还有需要注意的一点是，由于式（12）是非凸的，通过对式（12）的迭代优化得到的解不是全局最优解，而是一个局部最优解。但是，由于标准正交约束，它也是一个唯一解。该解渐近收敛于式（11）对应的解，因此式（11）的解也是局部唯一解。

4 实验结果分析

本章在5 个图像数据集和3 个UCI 数据集上，将本文的NMF-JRMLPC 算法和K-means、PCA、NMF、GNMF 和RMNMF 进行比较，从而评价本文算法的性能。表1总结了实验中用到的数据集的参数信息。

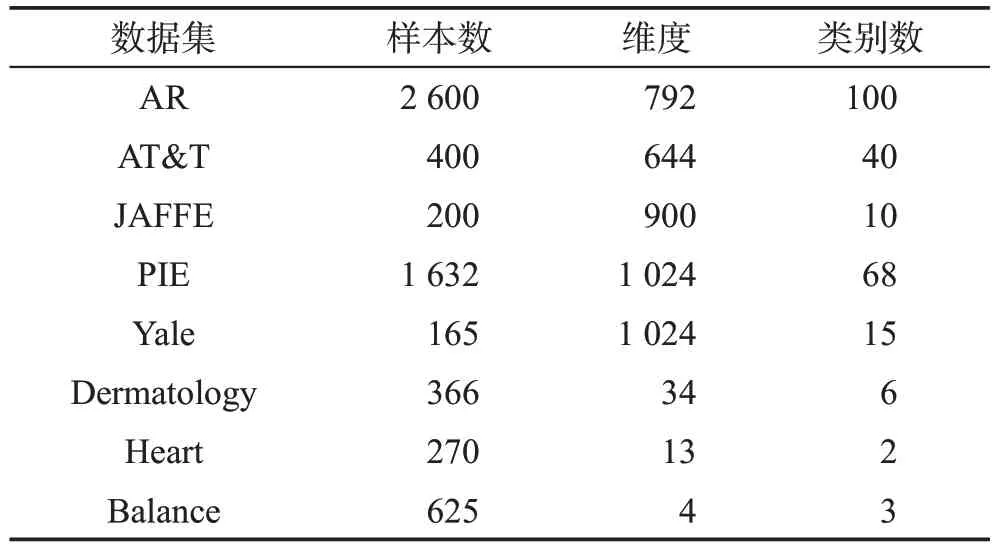
Table 1 Description of datasets表1 数据集描述

选取AT&T人脸数据集中第5到第8个文件夹中的图像数据，其中各类样本数量为10 张并统一尺寸为28×23，如图1所示。之后，在这些人脸图像中随机加入7×7 的遮挡区域来模拟真实世界的噪声数据，如图2所示。将本文的基于l2,1范数的NMF聚类模型与传统的基于l2范数的NMF聚类模型应用于这些有遮挡图像中，并比较聚类结果。为了进一步验证本文算法模型对有噪声干扰图像的识别效果，在这些人脸图像中随机加入椒盐噪声，加噪之后的图像数据如图3所示。

Fig.1 Original AT&T face image data图1 原始的AT&T人脸图像数据

4.1 参数设置

Fig.2 Occluded AT&T face image data图2 有遮挡的AT&T人脸图像数据

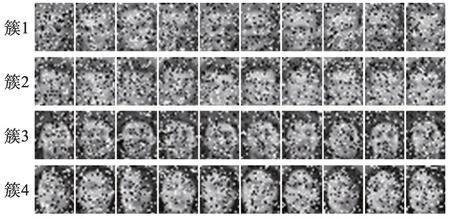
Fig.3 AT&T face image data with salt&pepper noise图3 加入椒盐噪声的AT&T人脸图像数据

对于图正则化的矩阵分解算法（即GNMF、RMNMF），使用0-1 权重的数据图，并且根据原文献设置近邻数寻优区间在{1,2,…,10}之间，正则化参数的寻优区间在{0.1,1,…,1 000}之间。由于K-means算法、PCA 算法和NMF 算法没有任何参数可以进行选择，因此只需给定聚类的簇个数即可。对于NMFJRMLPC 算法，初始化Γ,Σ∈0n×p，μ=0.001，ρ=1.05。然后设置正则化参数的寻优区间在{0.001,0.01,0.1,1,10,100}之间，近邻数寻优区间在{1,2,…,10}之间。对于所有的数据集，都随机采样10%的样本点来构造成对约束矩阵。最后，在每个数据集上运行所有算法20次，并记录结果进行比较。

4.2 在实验数据集上的聚类结果分析

使用归一化互信息（normalized mutual information，NMI）[27]和芮氏指标（Rand index）[28]作为聚类结果的评价指标。两种评价指标的取值范围均为[0，1]，值越大表明算法的聚类性能越好。6 种算法在本文的实验数据集上的聚类结果对比如表2所示。从表2中可以看出，本文算法的聚类性能在多数数据集中都优于其他5 个对比算法。这就意味着本文算法结合有效利用成对约束信息和充分学习样本结构信息这两方面的正确性和有效性。特别需要注意的是，AR和PIE这两个数据集中的图像中都包含着大量遮挡区域和不同光照引起的干扰，而从结果中可以看出：本文的NMF-JRMLPC 算法相对其他算法都表现出了较大的性能优势。这就证明了基于l2,1范数的目标函数对噪声和干扰所具有的鲁棒性。此外，表3中对有遮挡图像的聚类结果更进一步地说明了这一点。

Table 2 Clustering results of 6 algorithms表2 6种算法聚类结果

图4展示了NMF-JRMLPC算法在加入椒盐噪声的AT&T图像数据上的聚类结果。如图4可见，本文算法将所有图像分成的4 个簇中都包含着相同类别的图像。因此，进一步证明了本文的算法不易受噪声数据的干扰。

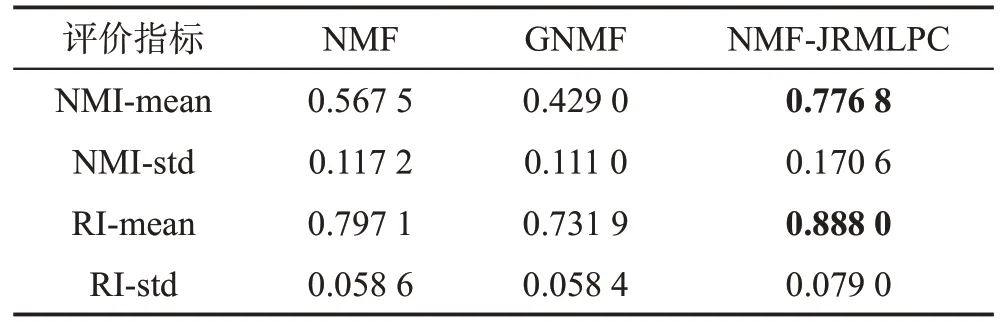
Table 3 Clustering results on occluded images表3 在遮挡图像上的聚类结果

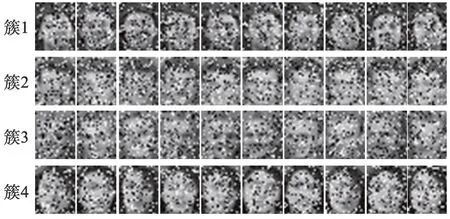
Fig.4 Clustering results of NMF-JRMLPC on noise image图4 NMF-JRMLPC算法在噪声图像上的聚类结果

4.3 权衡系数τ 的影响分析

本节研究了成对约束项与流行正则化项的权衡系数对聚类精度的影响。如前所述，本文算法通过使用一个在固定区间[ 0,1) 内变的权衡因子τ来控制成对约束对图拉普拉斯的影响程度。图5 展示了当固定其他参数时，τ从0.1到0.9之间的变化对聚类结果产生的影响。从图5 中可以看出：AR、AT&T、PIE和Heart 数据集对权衡系数τ存在着一定的鲁棒性，它们的聚类结果随着权衡系数的变化表现得较为稳定；而在JAFFE、Yale、Dermatology 和Balance 数据集中，聚类精度随着权衡系数的变化而不断波动，这就体现了成对约束对图拉普拉斯矩阵的调节作用。因为很难得到对数据流形的无偏估计，并且从给定的数据标签转换而来的成对约束通常具有较高的置信度，于是这种类型的调节就起到了一种校正的作用。通过这种灵活的参数调整，能够进一步提升半监督学习模型的性能。

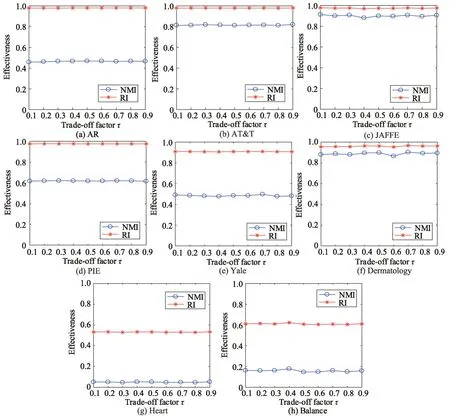
Fig.5 Clustering results with varyingτ values图5 不同τ 值的聚类结果

5 结束语

本文通过样本中包含的少量成对约束信息来构造成对约束矩阵，并结合流形学习的知识，提出了流形学习与成对约束联合正则化非负矩阵分解聚类方法（NMF-JRMLPC）。本文的目的是通过有效利用实际应用中存在的有限监督信息和充分探索样本中的结构信息来提升NMF算法的聚类准确性；同时，使用基于l2,1范数的损失函数来减少数据中噪声的影响程度并保持数据向量的特征旋转不变性。另外，本文提出的流形与成对约束联合正则化框架不只是流形与成对约束正则化的简单组合，它还利用了成对约束对图拉普拉斯的隐式调节，从而能够促进对真实数据流形的无偏差近似。