基于改进的HMM地图匹配算法
2020-07-09张浩刘大明
张浩 刘大明


摘 要:针对路网拓扑结构的复杂和轨迹信息利用不充分问题,文章提出了一种改进的HMM,该方法考虑了真实路网的拓扑信息,轨迹的位置、方向和速度信息。在计算发射概率时用二维正态分布将轨迹的位置信息和方向信息融合,转移概率计算时考虑到候选道路的限制速度和距离的非线性关联,并在实验中得到验证,改进后的匹配成功率比传统HMM提高了7%。
关键词:拓扑结构;HMM;观测概率;转移概率
中图分类号:TP301.6 文献标识码:A 文章编号:2096-4706(2020)21-0084-04
The Map Matching Algorithm Based on Improved HMM
ZHANG Hao,LIU Daming
(School of Computer Science and Technology,Shanghai University of Electric Power,Shanghai 200090,China)
Abstract:In view of the complexity of road network topology and inadequate utilization of track information,an improved HMM method is proposed in this paper,which considers the topology information,track position,direction and velocity information of the real road network. In the calculation of the emission probability,the location information and direction information of the trajectory are fused together with the two-dimensional normal distribution. In the calculation of the transition probability,the nonlinear relation between the limit speed and distance of the candidate road is taken into account,which is verified in the experiment. The improved matching success rate is 7% higher than the traditional HMM.
Keywords:topology;HMM;observation probability;transition probability
0 引 言
随着无线通信技术和定位技术的发展,轨迹数据可用于空间数据挖掘、智能交通[1-3]、城市规划[4,5]等领域。近年来学者在地图匹配算法或技术方面做了大量的研究。Quddus等人将其归纳为四种类型:基于几何的算法、基于拓扑的算法、基于概率的算法和基于高级数学理论的算法[6]。基于几何的算法主要考虑路网和轨迹的几何特征,如点对点[7]、点对线[8]和线对线算法[9],但是基于几何的算法通常会忽略拓扑信息,这可能导致复杂场景的错误匹配;基于拓扑的算法则侧重于轨迹和路网之间的拓扑关系[10],包括拓扑加权算法[11]、地图匹配算法[12]和加权地图匹配算法[13],这类算法将路网处理为图结构,从而将拓扑信息纳入其中,适用于高采样率的地图匹配算法;基于概率的算法将GPS位置视为随机变量,轨迹视为随机过程。HMM是这些算法中常用的算法。基于HMM的方法非常适合道路匹配[14],HMM可以同时考虑几何和地形信息,却不需要训练数据,但是该算法对最短路径进行计算使得计算开销很大。位置和方向信息不符合严格的独立分布,因而HMM的发射概率计算公式并不适用于地图匹配。模糊逻辑[15]、神经网络[16]、卡尔曼滤波[17,18]、粒子滤波和Dempster-Shafer[19]理论等先进的数学和人工智能理论在地图匹配领域广泛应用,但是此类算法通常需要大量的训练数据集来执行逐点匹配,使得它们的实际应用非常困难。
基于此,作者提出了一种改进的HMM方法并应用于地图匹配,该方法不仅考虑了路网的拓扑信息,轨迹的位置和方向信息,还在计算发射概率时将轨迹的位置信息和方向信息融合,转移概率计算时考虑到候选道路速度和距离的关联,并从数学的角度对匹配问题进行了研究。该方法在降低计算成本、减轻拓扑误差对路网的影响方面具有明显的优势。
1 地图匹配问题
1.1 建立路网
路网数据一般是shapefile格式,通过读取shp文件和dbf文件,获取道路的节点ID、坐标信息及属性信息,从而建立路网的有向图G(V,E),其中V的元素为道路端点,E的元素為道路路段。
1.2 地图匹配问题
本质上匹配问题可以推广为一个优化问题,在给定条件下寻找匹配的最优解。对应的GPS测量值g可定义为物理位置x和误差λ的叠加。对单一的轨迹点进行各种形式观测概率的计算,忽略了轨迹点的前后关联。
为了分析轨迹点与路网的对应关系,假定对应关系为:
g=x+λ (1)
其中,x∈r,r∈R,且r为路段,R为所有路段的集合,λ为GPS测量误差。为了说明,式(1)可以写成:
(2)
其中,x1∈r1,x2∈r2,…,xn∈rn和r1∈R,r2∈R,
…,rn∈R,因此匹配问题可以转化成以下目标函数:
或者
解决地图匹配问题包括为每一个GPS测量值在真实道路上找到一个最优的匹配点。在本研究中,我们将目标函数重新定义为随机过程:
(3)
其中,p(xi+1=si+1|xi=si)是指在前一个轨迹匹配概率最大的前提下下一个轨迹点选择路段的概率,si为候选路段。
在匹配概率最大的情况下,寻找一个最优映射集使得{si|i=1,2,…,n}取得最大匹配概率。
观测概率用来描述一个GPS测量值g对应一个候选状态x的可能性有多大,可以通过考虑位置和方向信息表示为条件概率:
Po(g)=p(x=xo|g,xr=gr|gr) (4)
其中,xr为轨迹方向信息。
Newson等认为观测到的轨迹点符合正态分布,可以使用高斯函数来表达距离因素的发射概率,本文考虑到轨迹点的距离、方向、速度三者之间具有很大的關联,所以采用的是二维正态分布表示观测概率,计算公式为:
(5)
其中,,,μ1为从轨迹点至候选路段的均值,μ2为GPS设备的系统误差,σ1为GPS的误差的标准差,一般取值为20,σ2为方向观测误差的方差,ρ均为常数,且σ1>0,σ2>0,|ρ|<1则称(x,y)服从参数为μ1,μ2,σ1,σ2,ρ的二维正态分布,记作(x,y)~N(μ1,μ2,σ12,σ22,ρ)。
d(x-g)=‖x-g‖ (6)
其中,d(x-g)为点到路段的距离。
假定 为速度方向与匹配路段的夹角。以正北方向为基准,计算速度与正北方向的夹角为βi,匹配路段与正北方向的夹角分别为 ,则 计算公式为:
(7)
为此本文将转移概率用式(8)表示:
(8)
其中,xi+1为第i+1个轨迹点,xi为第i个轨迹点对应的候选路段;ω1+ω2=1,其中ω1>0,ω2>0;v为所选路段的限速;Dis为从候选路段间的实际路网距离。区别于使用传统的BFS算法(如Dijkstra算法),本文使用启发式的A*算法进行路网距离的计算。A*算法不需要遍历路网中所有的路段,其距离估算值与实际值越接近,算法运行速度越快,效率越高。
2 算法模型与分析
2.1 数据集描述
本文的轨迹数据来源于北京市二环周围100辆出租车,24 860条GPS数据[20],此数据集的GPS轨迹由带有时间戳的点序列表示,每个点包含纬度、经度、速度和方向信息。缓冲区半径R设为200 m。
地图匹配的准确率为:
(9)
其中,acc为准确率,m为正确匹配到对应路段的轨迹点的个数,j为轨迹点的总数。
2.2 实验分析
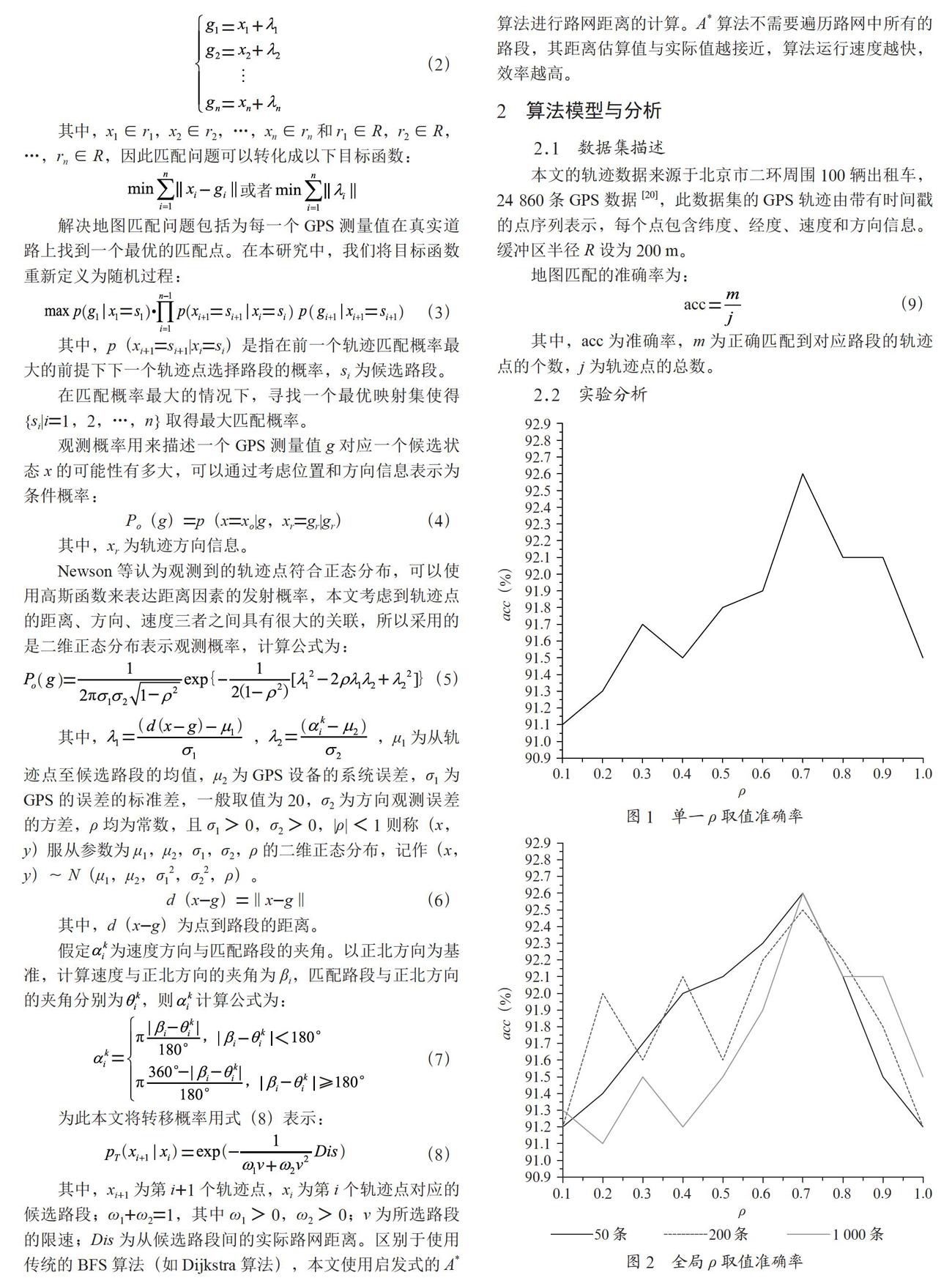
在计算观测概率时选择二维正态分布作为概率公式,其中的μ1,μ2,σ1,σ2,ρ参数有些是基于经验,有些是路网数据分析而来,其中ρ参数是反应距离和方向关联度大小的关键指标,在实验中以线性递进验证取值ρ为多少时轨迹匹配率最高,如图1、图2所示。
分别选择50,200,1 000条轨迹分析相关系数ρ取值的适用性,计算每组实验的匹配准确率平均值,如图2所示。从图1和图2中可得在计算观测概率时ρ的取值虽然对匹配准确率的影响很大,但是总体的准确率依旧很高,可以发现当ρ取值为0.7时,匹配效果最为显著。
当ρ取值为0.7,转移概率选用经典计算公式时,对比本文算法和HMM的匹配准确率,如表1所示。
考虑到距离和方向的关联性,并通过实验分析确定了关联度参数的取值,表1中的结果证明了匹配的准确率提高了2.58%。
当ρ取值为0.7时,我们选择一条轨迹分析ω取值对匹配准确率的影响,实验结果如图3、图4所示。
为了避免匹配偶然性的发生,分别选择50,200,1 000条轨迹分析ω取值的适用性,分别计算每一条轨迹的匹配准确率,总轨迹数叠加取其平均值,如图3所示。
从图3和图4可得随着ω取值的增大,准确率相对的增大,在相关系数ω为0.6时,轨迹匹配正确率的最大,随后便不断地下滑。本文选择ω为0.6作为实验的最终参数。匹配的准确率有些许波动,原因可能是真实路网中的某些路段没有收录在地图数据中,或是待匹配轨迹过度分散和漂移严重。
为此我们对本文所选用的数据集做了总体的预测,并将本文算法和原始HMM进行对比,如表2所示。
由表2可得,本文算法比原始的算法在匹配准确率上提高了7.12%,效果非常显著。
本文截取了部分出租车在一定时间段内的行驶轨迹点匹配到道路网的情况,其匹配结果如图5、图6中加粗的黑线所示。
从图5和图6中可以看出本文提出的地图匹配算法不仅适用于短路径匹配还在长轨迹段取得了优异的效果。
3 结 论
在地图匹配的研究中,本文提出了一种改进HMM地图匹配算法。在计算观测概率时兼顾了位置和方向的关联性,转移概率计算中将速度因素纳入考虑。结果表明,该算法的准确率可达97%。虽然我们的算法很大程度上依赖于详细正确路网数据,但仍在复杂路段取得了高精度的匹配。需要注意的是是该算法仍会受到相邻平行路段或多车道的干扰,候选路段的精确快速搜索以及驾驶人的行车习惯等因素的影响,上述问题是未来研究的潜在重要课题。
参考文献:
[1] YUAN J,ZHENG Y,XIE X,et al. Driving with knowledge from the physical world [C]//Proceedings of the 17th ACM SIGKDD international conference on Knowledge discovery and data mining.New York:Association for Computing Machinery,2011:316-324.
[2] CHEN C,ZHANG D Q,CASTRO P S,et al. iBOAT:Isolation-based online anomalous trajectory detection [J].IEEE Transactions on Intelligent Transportation Systems,2013,14(2):806-818.
[3] LI X L,HAN J W,LEE J G,et al. Traffic density-based discovery of hot routes in road networks [C]//Proceedings of the 10th international conference on Advances in spatial and temporal databases.Berlin:Springer-Verlag,2007:441-459.
[4] ZHENG Y,LIU Y C,YUAN J,et al. Urban Computing with Taxicabs [C]//Proceedings of the 13th ACM International Conference on Ubiquitous Computing.New York:Association for Computing Machinery,2011:89-98.
[5] ZHANG J T. Smarter outlier detection and deeper understanding of large-scale taxi trip records:a case study of NYC [C]//Proceedings of the ACM SIGKDD International Workshop on Urban Computing.New York:Association for Computing Machinery,2012:157-162.
[6] QUDDUS M A,OCHIENG W Y,NOLAND R B. Current map-matching algorithms for transport applications:State-of-the art and future research directions [J].Transportation Research Part C:Emerging Technologies,2007,15(5):312-328.
[7] KIM S,KIM J H. Adaptive fuzzy-network-based C-measure map-matching algorithm for car navigation system [J].IEEE Transactions on Industrial Electronics,2001,48(2):432-441.
[8] WHITE C E,BERNSTEIN D,KORNHAUSER A L. Some map matching algorithms for personal navigation assistants [J].Transportation Research Part C:Emerging Technologies,2000,8(1-6):91-108.
[9] PHUYAL A,BISHNU P. Adaptive trajectory segmentation method and its application in in-car navigation system [D].Ohio:The Ohio State University,2001.
[10] 張小国,王庆,万德钧.基于路网拓扑特性及先验知识的地图匹配算法 [J].东南大学学报(自然科学版),2006(4):625-629.
[11] 盛彩英,席唱白,钱天陆,等.浮动车轨迹点地图匹配及插值算法 [J].测绘科学,2019,44(8):106-112.
[12] QUDDUS M A,OCHIENG W Y,ZHAO L,et al. A general map matching algorithm for transport telematics applications [J].GPS Solutions,2003,7(3):157-167.
[13] HASHEMI M,KARIMI H A. A weight-based map-matching algorithm for vehicle navigation in complex urban networks [J].Journal of Intelligent Transportation Systems,2016,20(6):573-590.
[14] 高文超,李国良,塔娜.路网匹配算法综述 [J].软件学报,2018,29(2):225-250.
[15] 田甜,吕芳,王秀玲.一种基于浮动车优化地图匹配方法 [J].现代电子技术,2015,38(11):159-162.
[16] LI H Q,WU G. Map Matching for Taxi GPS Data with Extreme Learning Machine [C]//International Conference on Advanced Data Mining and Applications,2014:447-460.
[17] XU H,LIU H C,TAN C W,et al. Development and Application of an Enhanced Kalman Filter and Global Positioning System Error-Correction Approach for Improved Map-Matching [J].Journal of Intelligent Transportation Systems,2010,14(1):27-36.
[18] SMAILI C,NAJJAR M E B E,CHARPILLET F. A Hybrid Bayesian Framework for Map Matching:Formulation Using Switching Kalman Filter [J].Journal of Intelligent & Robotic Systems,2014,74(3-4):725-743.
[19] 王科,李鹏,金瑜,等.基于三证据DS理论的双模式地图匹配算法 [J].计算机工程,2018,44(5):316-321.
[20] 曾嘉郦,孙立双,王晓明.北京出租车GPS轨迹数据地图匹配算法研究 [J].北京测绘,2019,33(3):255-260.
作者简介:张浩(1996—),男,汉族,安徽蚌埠人,硕士研究生,主要研究方向:轨迹预测、物联网技术、嵌入式系统开发;刘大明(1971—),男,汉族,上海人,副教授,博士,主要研究方向:物联网技术、嵌入式系统与设计、智能工业机器人。
