基于信息熵的适应性随机测试用例生成算法分析

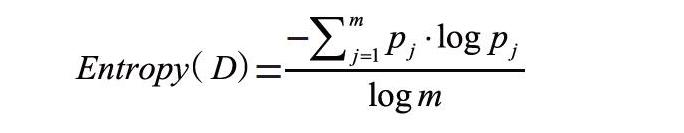
摘  要：文章对适应性随机测试理论基础进行分析，并在信息熵基础上对测试用例算法加以阐述，主要包括信息熵指标、算法应用、实证实验三项内容，通过文章研究可知，Entropy算法与其他算法相比，无论在高维还是低维空间情形下，均具有良好的失效检测能力。

关键词：信息熵;适应性随机测试;算法

中图分类号：TP301.6      文献标识码：A 文章编号：2096-4706（2020）02-0030-02

Abstract：This paper analyzes the theoretical basis of adaptive random testing，and explains the test case algorithm based on information entropy. It mainly includes three items：information entropy index，algorithm application，and empirical experiments. According to the research in this paper，Entropy algorithm and other compared with the algorithm，it has a good failure detection ability in both high-dimensional and low-dimensional space situations.

Keywords：information entropy;adaptive random test;algorithm

0  引  言

在信息时代背景下，计算机软件在技术产业得到广泛应用，对软件质量与可靠性提出严格要求，软件测试的地位不断提升。在软件测试过程中，测试用例选择十分重要，对测试效果具有直接影响。对此，应尽量采用典型用例，在信息熵的基础上采用适应性测试用例，引入FSCS-ART经典算法，提高揭错能力。

1  适应性随机测试的理论基础

1.1  随机测试

在软件测试方面，随机测试的应用范围较为广泛，测试时无需掌握程序中的内部结构与软件需求，只需在输入空间内部采用伪随机数生成器，便可对数据点进行自动化测试，具有成本低、自动化程度高、实施简便等特点。现阶段，软件种类不断增加，Unix工具集、Java程序、Windows GUI应用软件等在测试活动中得到普遍应用，还可与其他软件测试方法综合使用，如组合测试、回归测试等等。随机测试具有预测性，通过统计意义可对其检测能力进行分析，在此基础上的改进算法也随之产生。

1.2  FSCS-ART算法

在随机测试中，该方法属于第一个具体算法，受到软件工程领域的广泛关注。该算法适用于输入值为数值型的待测程序，利用用例候选策略，将候选用例与已测用例为标准，对多样性进行判断。在本文研究中，将该项指标定义为distance指标。据研究结果可知，在低维输入域中，ART中的F-measure值与随机测试相比降低，这意味着测试的失效检测力得到极大提升。

1.2.1  distance指标

该指标的具体定义为：给定候选用例集CS，其取值范围在c1，c2，c3，…，cs之间，以用例ci为例，指标计算公式為：

dis tance（ci）=dist（ci，η（ci，TS））

式中，TS代表的是已测用例集合;dist（ci，η（ci，TS））定义为数值程序中两个用例间的欧式距离;η（ci，TS）代表的是在TS集合中，与ci距离最近的用例。由上述公式可知，候选用例的指标主要是与全部已测用例之间距离最小的数值，该数值越大，意味着与已测用例的距离越长，区分度也就越大。因此，在ART算法中，dis tance的数值越大，说明候选用例中的优先级越高。

1.2.2  算法流程

在ART算法中，应将每次产生的候选用例、执行用例分别用两个集合进行存储，将CS与TS集合进行初始化处理。首先，从整个输入域中选出一个用例，当执行用例中无实效情况时，可将其输入到TS集合中，在第3～10行中循环，形成新的用例。在生成下一个用例之前，首先在输入域中随机生成s个候选用例，并将其存储在CS集合中。随机选出用例ci，i的范围在1～s之间，对其与TS集合中用例的最小距离进行计算，得出dis tance值，将其应用到后续实测用例中。对上述流程不断重复，直至与停止条件相符合，从而达到挖掘失效或已测用例数目预定值的目标[1]。

2  基于信息熵的随机测试用例算法分析

本文站在失效检测效果的视角，在高维环境下对ART算法进行改进，提出新的算法—FSCS-Entropy算法，以此获得更加理想的用例分布结果。同时，将信息熵与距离两项指标引入其中，对候选用例与已测用例的分散度进行绘制，以此降低边缘处用例优先级，使算法的失效检测性能得到进一步提升。

2.1  信息熵指标

该指标的主要作用在于解决信息量化度量问题，在信息工程领域应用较为普遍。在相关理论中，熵可对样本集合纯度进行衡量。假设集合D中第j类样本占比为pj，其中j的取值范围在1～m之间，则集合D信息熵的计算公式为：

如若集合中的样本类型为两种，信息熵与样本比例之间的变化呈曲线分布。当集合内不同样本发生概率均衡，也就是pj的数值为1/m时，集合中的信息熵数值处于最大值;当信息熵的最小值为0时，则意味着集合内部存在一类样本，其纯度较高[2]。

2.2  算法应用

针对FSCS-EntropyA算法进行分析，在该算法正式运行之前，应事先对各相关变量进行设置，即候选用例集大小，用s表示;待测程序的输入域，用R表示;准则k值以及输入域维度，用d表示。在算法应用过程中，先对TS和CS集合进行初始化，随后在程序中输入域中随机选择一个数据点，将其当作首个测试的用例，在待测程序中实施。对于首个新用例来说，如若没有发现失效情况，则在3～15行中反复循环，生成大量新用例，直至与停止条件相符合。当测试用例中均没有成功检测出失效时，可将其传入到TS集合中，在生成后续用例之前，先将其输入到域内，随机出现s个候选用例，并将其存入CS集合内。对于CS集合来说，其中包括的候选用例均为ci，先要对集合TS中的现有用例最短距离进行计算，将其记为dis tance（ci），然后利用该指标从CS集合中对最优k个候选用例进行选择，将其纳入到CS集合中，在第10～13行的位置对CS进行遍历。针对任意候选用例ci来说，可首先找出与之相距2d的邻居，将其记为Top-2d（ci），按照ci与上述邻居用例之间的距离进行计算，得出entropy指标。最后，利用CS集合中的最大entropy数值候选用例对后续测试用例进行计算。

在EntropyB算法的应用中，输入参数、初始操作与EntropyA之间的操作相同，IE大多数流程也较为相近，二者的不同之处在于B算法主要对CS集合中的各个候选用例ci进行计算，从中找出与之相距2d的邻居用例，用Top-2d表示，在此基础上对邻居用例间的距离进行计算，得出entropy指标，最后通过该指标从集合CS中选出最佳k用例，使其拥有最大值，应用到后续实测用例之中[3]。

2.3  实证实验

为了对Entropy算法在不同场景中的应用效果进行分析，本文提出以下实验问题：在失效实际程序中，Entropy算法与典型ART相比测试效果存在何种区别。

2.3.1  实验设置

在实证实验方面，本文采用25个经典程序，并采用Java语言进行实现，前14個程序由ACM收集算法提供，在适应性随机测试中得到普遍应用。在高维程序中，line、calDay与complex分别对点、线段、三角形之间的位置关系进行确定。对于上述几何程序来说，输入参数为点坐标、线段端点，select程序是从无序数组中取出的第k个最大元素，最后程序为tcas西门子防撞系统。对于不同的实际程序来说，失效率属于近似值，为了描述便利，采用F-measure指标对不同算法检测效果进行衡量。

2.3.2  失效检测效果

对高维实验结果进行对比可知，Entropy算法的检测效果与ART算法相比较差。通常情况下，前者中的measure数值均小于后者的对应值，将二者的p-value进行进一步对比可知，对于大多数实际程序来说，p-value数值均超过0.05，这意味着二者在失效检测能力方面无明显差异。另外，在plgndr程序中measure数值为552.76、binaryGCD程序中measure数值为1345.71，Entrop算法中measure数值为845.50，但是在ART算法中，三者对应的数值分别为603.19、1626.94与998.72。由此可见，在上述程序中，Entropy算法中的measure数值低于ART算法，且p-value的数值低于0.05，这充分表明Entropy算法具有较强的失效检测能力。此外，在低维程序中，与ART算法相比，Entropy算法的数值较低，且二者p-valur远远低于0.05，同样说明该算法在低维状态下的检测能力。

3  结  论

综上所述，在软件测试领域中，自动化测试在操作性、效率等方面具有更多优势。在众多测试用例生成方式中，随机测试更加简单高效、易于实现，应积极将Entropy算法应用到高维或者低维空间情形中，使失效检测效果得到进一步提升，为软件测试开展提供充足的技术支持。

参考文献：

[1] 李万庆，李彦苍.求解复杂优化问题的基于信息熵的自适应蚁群算法 [J].数学的实践与认识，2005（2）：134-139.

[2] 纳春宁.基于图像信息熵的自适应Harris角点检测算法 [J].内蒙古农业大学学报（自然科学版），2013，34（5）：141-144.

[3] 余绍蓉，尹益辉，徐兵，等.基于信息熵理论的随机—模糊可靠性分析方法探讨 [J].机械强度，2006（5）：695-698.

作者简介：孙德刚（1978.04-），男，汉族，山东德州人，高级工程师，学士学位，研究方向：教育信息化、软件开发。