最值问题的求解策略
2020-07-09朱丽
朱 丽
(江苏省梁丰高级中学,215600)
最值问题是高考数学命题的热点,其考题方式呈多元化,既有选择题或填空题,又有解答题,设问灵活,综合性强,注重考查分析问题和解决问题的能力,具有一定的难度.本文着重分析高中数学中涉及主要知识点的几个最值问题,供参考.
一、一元函数的最值
“导数法”是解题的主要方法,如果是二次函数或简单的分式函数,也可考虑用“配方法”或“均值不等式”法.



点评 用导数求一元函数的最值,解题过程可以程序化,即先求导,求驻点,再判断函数单调性,然后将驻点代人函数式求出最值.
二、多元函数的最值
一般是运用“均值不等式”整体求出最值.如果条件允许,也可以通过消元转化为一元函数的最值问题.
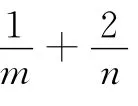

点评 有些已知条件中给出了等式条件,运用此等式是解题的关键,此题的结构极为精巧,条件等式比较隐含,通过找出定点就使问题变得真相大白了.
三、三角函数的最值
一般是将条件式化为一个复合角的三角函数式,利用正弦、余弦函数的有界性求最值,或转化为复合二次函数问题求解.
例3 (2008年四川高考题)求函数y=7-4sinxcosx+4cos2x-4cos4x的最大值与最小值.
解析 7-4sinxcosx+4cos2x-4cos4x=7-2sin 2x+4cos2x(1-cos2x)=7-2sin 2x+4cos2xsin2x=7-2sin 2x+sin22x=(1-sin 2x)2+6.由于sin 2x∈ [-1,1],且函数y=(1-x)2+6在[-1,1]上单调递减,当sin 2x=-1时,函数y有最大值(-1-1)2+6=10;当sin 2x=1时,函数y有最小值(1-1)2+6=6,即函数的最大值10,最小值6.
点评 求三角函数的最值是高考中最常见的题型,一般都是中档题.利用三角公式化简三角函数式是解题的重点.
四、实际应用问题中的最值
根据条件建立目标函数,可变为一元函数或三角函数最值问题,但要注意自变量的取值范围.
例4 (2004年全国高考题)某轮船航行过程中每小时的燃料费与其速度的立方成正比,已知当速度为10千米/时时,燃料费为10元/时,其他与速度无关的费用每小时180元. (1)轮船的速度为多少时,每千米航程成本最低?(2)若轮船限速不超过20千米/时,求每千米航程的最低成本.


点评 抓住题中的速度、时间、费用之间的数量关系,可以得到关于每千米航程成本的分式型目标函数.观察对比此题的两小题,可以发现函数自变量范围对求解优化问题方法选择上的影响.
五、平面区域中的最值
利用平面区域,数形结合解题.


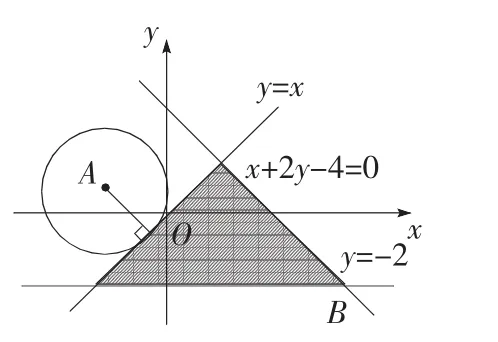
图1
点评 抓住问题的几何特征,或分析问题的几何背景,以形助数、以形解数是中学数学的重要思想方法.
六、数列中的最值
根据数列的性质,结合一些代数求最值的方法来求解.
例6 已知数列{an}的通项公式an=-2n3+24n2+18n+2,(n∈N),求数列的最大值项.
解析 ∵an+1-an=-2(n+1)3+24(n+1)2+18(n+1)+2-(-2n3+24n2+18n+2)=2n(21-3n)+40,当n≤7时,an+1-an≥0,即an+1≥an,当n≥8时,an+1-an<0,即an+1<an,∴数列{an}的最大值项可能为a7或a8,经计算知a8=658为最大值项.
点评 在数列{an}中,若an为最大值项,则an≥an+1且an≥an-1;若an为最小值项,则an≤an+1且an≤an-1.由此可列出不等式组求出正整数n.
七、立体几何中的最值
运用立体几何知识,分析线面关系及数据结论,通过建立目标函数求解.
例7 二面角α-CD-β的度数为θ,A为α上一点,△ADC面积为S,且DC=m,过A点作直线AB交半平面β于B,使AB⊥DC,且与半平面β成30°角,当θ为何值时,△BCD的面积取最大值,并求出最大值.

图2

点评 用三角知识解决立体几何中的求值问题是常见形式,同样用三角知识帮助解决有关的最值问题也是正确的选择.
八、解析几何中的最值
将解析几何问题函数化,再用函数求最值的方法解题.


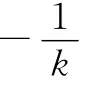
(2)当k=0时,MN为椭圆的长轴,

点评 在分析题意的基础上,通过转化向量关系,再利用斜率的相关运算建立了关于面积的函数关系,为后续解题指明了方向.
