布尔莎模型病态方程组解算的程序设计与实现
2020-07-09郑文霞
李 杰, 郑文霞
(湖北省地质局 第一地质大队,湖北 大冶 435100)
中国幅员辽阔,各地方使用的大地坐标系各不相同,由于历史原因造成有1954年北京坐标系、1980西安坐标系、地方独立坐标系等。根据《国土资源部国家测绘地理信息局关于加快使用2000国家大地坐标系的通知》(国测资发[2017]30号)的要求,于2018年6月底之前完成国土资源数据转换到国家2000坐标系,由于各坐标系统使用的椭球参数不同、椭球定位定向不同,因此没有一个严格的数学转换模型进行全面的转换,只能进行空间相似变换的方式求解出变换参数,再进行坐标转换。常用的转换模型有布尔莎、平面四参数、三维七参数、二维七参数等模型。
病态问题是指输入数据有微小误差引起输出数据相对误差很大,病态方程组是方程组的系数矩阵和常数项矩阵有微小误差,造成方程组的解不稳定;而方程组的病态程度可以用矩阵的条件数来衡量[1]。
本文主要探讨布尔莎模型及其产生病态方程组的原因和求解方法,并用VC++语言编程实现参数的求解过程。
1 布尔莎模型及其适用条件
布尔莎模型是假设了三个旋转参数εX、εY、εZ均为微小转角后的坐标转换模型,其模型[2]如下:
(1)
式中:△X0、△Y0、△Z0为三个平移参数;m为比例因子。
由于假设了三个旋转参数为微小角度,就限制了布尔莎模型的使用范围,一般在独立坐标系、地方坐标系中等旋转角较大的坐标转换时,该模型就不适用了。
另外,布尔莎模型适宜进行省级及以上大范围坐标转换,对于局部小范围的转换容易产生病态方程组,使得转换参数求解和转换结果不稳定。
2 布尔莎模型的误差方程及其程序实现
2.1 误差方程组成
(2)
式中:a1=a4εX;a2=a4εY;a3=a4εZ;a4=1+m。
2.2 误差方程程序设计的实现
根据公式(2)的误差方程,可编程实现系数矩阵和常数项矩阵元素的计算。
(1) 误差方程系数项计算的程序实现关键代码。
int k=0;
for (i=0;i { *(pA+k++) = 1; *(pA+k++) = 0; *(pA+k++) = 0; *(pA+k++) = 0; *(pA+k++) = 0-*(coordS_h+i); *(pA+k++) =*(coordS_y+i); *(pA+k++) =*(coordS_x+i); *(pA+k++) = 0; *(pA+k++) = 1; *(pA+k++) = 0; *(pA+k++) =*(coordS_h+i); *(pA+k++) = 0; *(pA+k++) = 0-*(coordS_x+i); *(pA+k++) =*(coordS_y+i); *(pA+k++) = 0; *(pA+k++) = 0; *(pA+k++) = 1; *(pA+k++) = 0-*(coordS_y+i); *(pA+k++) =*(coordS_x+i); *(pA+k++) = 0; *(pA+k++) =*(coordS_h+i); } (2) 常数项计算的程序实现关键代码 int j=0; for (int i=0;i< PointCount; i++) 常数项数组计算 { *(pL+j++)=*(coordT_x+i)-*(coordS_x+i); *(pL+j++)=*(coordT_y+i)-*(coordS_y+i); *(pL+j++)=*(coordT_h+i)-*(coordS_h+i); } CMatrix_cal为矩阵计算类,mat_A为误差方程系数矩阵,mat_L为误差方程常数项矩阵,mat_AT为转置矩阵,mat_ATA为法方程系数阵,mat_ATL为法方程常数项矩阵。程序实现如下: CMatrix_cal mat_AT(7,PointCount*3); mat_AT=mat_A.Transpose(); CMatrix_cal mat_ATA(7,7); mat_ATA=mat_AT*mat_A; CMatrix _cal mat_ATL(7,1); mat_ATL=mat_AT*mat_L; 由公式(2)可知法方程系数矩阵是一个非奇异的对称方阵,其矩阵元素之间相差数量级很大[3],如果进行局部小范围坐标转换,公共控制点的纵横坐标差异不大,则矩阵元素行向量相关性很强(近似线性相关),导致法方程系数矩阵接近奇异阵,矩阵求逆结果很不稳定[4],这样,公共点有很小的误差将直接导致法方程常数项的变化,系数矩阵的病态程度严重程度,将影响法方程解的误差大小[5]。 要判定法方程系数矩阵的病态程度,可利用矩阵的条件数来衡量[6]。 矩阵的条件数的大小,决定了矩阵是“良态”还是“病态”,一般矩阵的条件数远>1时(经验值为100),为中度病态,条件数>1 000时为较严重病态,条件数越大表明病态越严重[7]。 而矩阵的条件数与矩阵的范数有关,由矩阵范数的定义,可以用矩阵的行范数、列范数和2-范数来计算,其中: (3) (4) (5) 这里给出行范数的VC++关键程序代码如下: double max_sq=0; for (int v=1;v<=7;v++) { for (int w=0;w<7;w++) { sq=sq+abs(*(ATA+qw)); qw++; } s[v]=sq; if (s[v]>=max_sq) max_sq=s[v]; sq=0; } 同样,也可以用列范数和2-范数编程实现条件数的计算,这里不再赘述。 对于布尔莎模型可能产生的病态法方程(非严重病态),可利用迭代改善法[8]编程求解,具体求解步骤为: ① 利用“全选主元高斯消去法”求解未知参数(即七参数)的近似解X(1); ② 代入X(1),求余向量R=B-AX(1)的值; ③ 求解AQ=R,求取Q向量的值,然后X(2)=X(1)+Q; ④ 使X(1)=X(2),重复②至④,给定一个微小量ε, 上述①中的“全选主元高斯消去法”很多参考书可找到,这里将其成员函数命名为GetRootGuass()。病态方程求解程序实现的关键代码[9]如下: CMatrixTestDlg les(matrixCoef,matrixConst); if (! les.GetRootGuass(matrixResult)) return false; double* x = matrixResult.GetData(); q=1.0+eps; while (q>=eps) { if (i==0) return false; i=i-1; CMatrix_cal matrixE = matrixCoef*matrixResult; CMatrix_cal matrixR = matrixConst - matrixE; CMatrixTestDlg les(matrixCoef,matrixR); CMatrix_cal matrixRR; if (! les.GetRootGuass(matrixRR)) return false; double * r = matrixRR.GetData(); q=0.0; for ( k=0; k<=n-1; k++) { qq=fabs(r[k])/(1.0+fabs(x[k]+r[k])); if (qq>q) q=qq; } for ( k=0; k<=n-1; k++) x[k]=x[k]+r[k]; } 这里模拟一套原坐标系和目标坐标系下公共控制点的坐标数据,作为算例如图1和图2。 图1 原坐标文件Fig.1 Original coordinate file 图2 目标坐标文件Fig.2 Target coordinate file 程序主界面如图3。 图3 程序主界面 根据程序计算得法方程系数阵见图4。 图4 法方程系数矩阵 行范数(条件数)计算结果见图5。由行范数(条件数)为1.7×109量级,可见其病态较严重。利用上述程序,七参数计算结果如图6。 图5 条件数计算Fig.5 Condition number calculation 图6 七参数计算Fig.6 Seven parameters calculation 转换后各控制点的残差见图7。若在A7点上X、Y、Z三个坐标分量上均减去4cm(模拟误差),重新计算参数和残差,则计算的残差值如图8。 图7 坐标残差计算结果 图8 加入模拟误差后的坐标残差计算结果 由残差值可见,虽然法方程系数阵病态严重,公共控制点存在较大误差,但是利用求解病态方程组的方法,编程实现布尔莎模型的参数求解,求得的参数精度高(除A7点,其余点基本上是毫米级转换精度),坐标转换成果稳定。 布尔莎模型参数的求解,需要多次计算,逐步剔除有粗差的公共控制点,求得较好的参数,但要保障转换范围内公共控制点的总体数量和点位分布情况,还要注意以下几个问题:①该模型仅适合微小旋转角的坐标系之间的坐标转换;②该模型适合进行大范围(省级及以上)坐标系之间的坐标转换;③利用病态方程组求解方法能有效地提高参数求解的精度和可靠性;④非公共控制点的转换应尽量位于公共控制点的范围内。 本文通过VC++编程实现了上述求解过程,在生产实践中得到了验证,为提高成果转换精度和工作效率,起到了很大的作用。3 布尔莎模型的法方程组成
3.1 法方程系数及常数项计算的程序实现
3.2 法方程系数矩阵产生病态的原因
3.3 法方程系数矩阵的条件数



4 布尔莎模型的病态法方程解算

5 算例



Fig.3 Main interface of program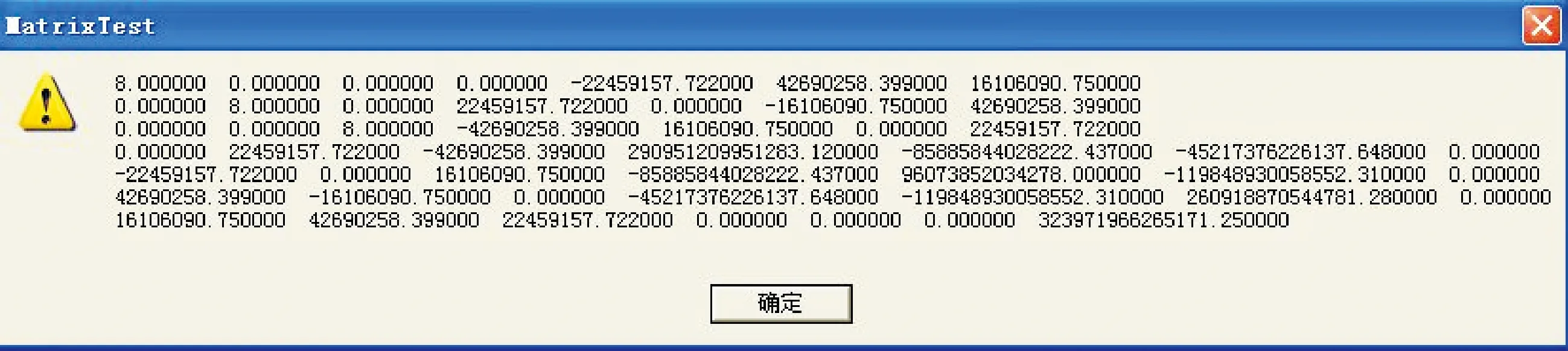
Fig.4 Coefficient matrix of normal equation
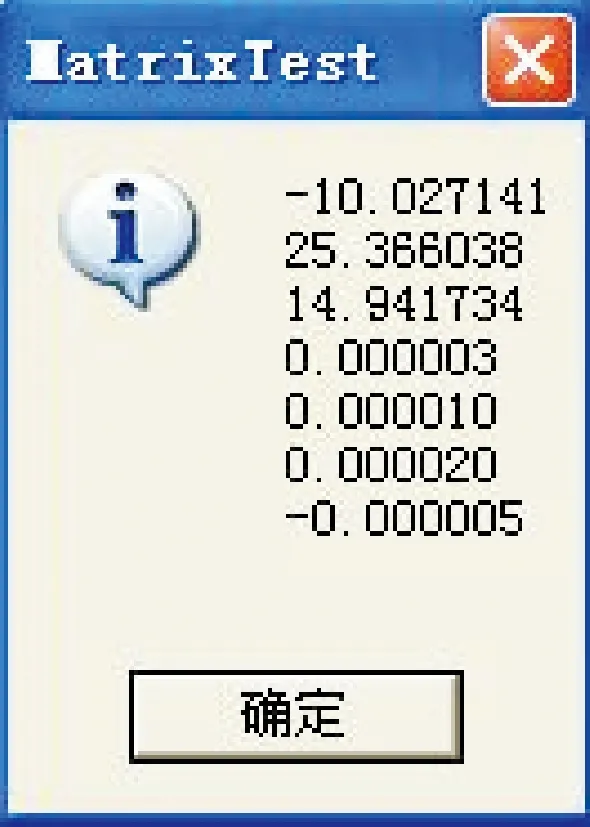
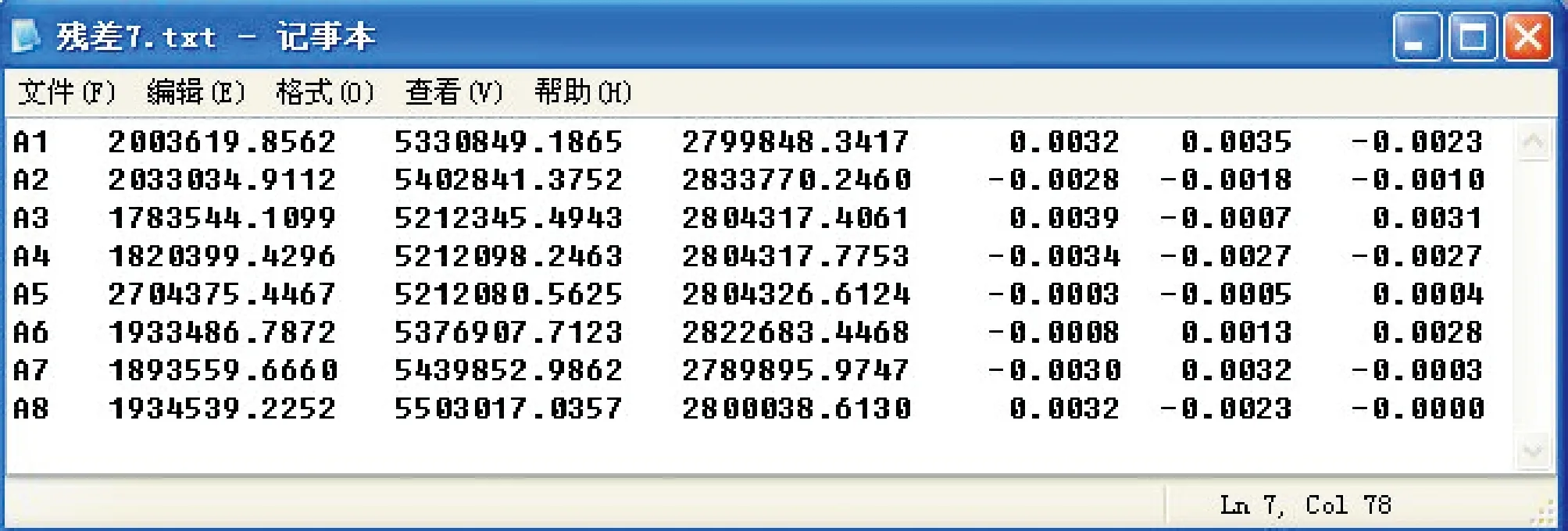
Fig.7 Calculation results of coordinate residuals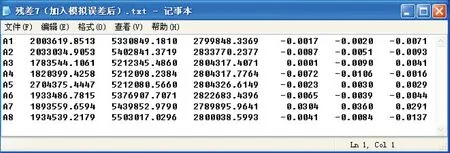
Fig.8 Calculation results of coodinate residual error after adding simulation error6 结语
