基于复数矢量分析的汽车起重机液压变幅机构优化设计
2020-07-09房秋怡周伟刘鹏段克军
房秋怡,周伟,刘鹏,段克军
(武警士官学校,杭州 311400)
引言
汽车起重机广泛应用于交通运输行业和建筑业,尤其在建筑业工程建设领域中得到广泛应用。比如在大型建筑物构建与设备安装过程中,使用大量工程材料能够垂直运输与装卸货物。液压变幅机构作为汽车起重机重要组成部分,不同部位铰点的布置方法以及液压变幅油缸位置对汽车起重机工作效率影响甚大[1]。在传统汽车起重机液压变幅机构设计中,通常采用类比法,并加以手工绘图方法确定铰点位置,整个设计周期较长,无法满足当代人们对于汽车起重机设计的高标准要求,严重制约了产品更新换代的速度[2]。液压变幅机构参数设计的合理性,对汽车起重机的结构稳定性及其整体性能带来直接影响。
当前,汽车起重机液压变幅机构设计理念较为落后,其机构中的角位置、角速度及角加速度与机构的实际运动规律存在较大的误差。为了解决传统设计方式存在的问题,将汽车起重机变幅机构作为优化对象,把机构视为封闭矢量多边形,采用复数方式描述该机构矢量方程式,并建立直角坐标,选取投影,实现基于复数矢量分析的汽车起重机液压变幅机构优化设计。
1 汽车起重机液压变幅机构优化
汽车起重机液压变幅机构主要结构包括主臂、转台、变幅油缸,在中心吨位汽车起重机中各个部分结构基本一致,为了对汽车起重机液压变幅机构优化,需对主臂、转台以及液压变幅三铰点进行优化设计[3]。汽车起重机液压变幅机构模型简图如图1所示。
在模型构建中,需利用Pro/E软件建立截面臂架、变幅液缸、回转平台的三维模型。将该文件保存后,直接导入虚拟样机环境之中,并在该环境中设置组件材料和质量,通过添加相对驱动约束条件,对汽车起重机液压变幅机构主臂、转台以及液压变幅三铰点进行优化[4]。
1.1 汽车起重机主臂优化
在汽车起重机液压变幅机构优化过程中,需先确定相关关键变量,并将这些变量设置为基本变量。在分析过程中,只需改变设计变量值大小,就能对主臂主要参数自动优化。
针对主臂结构优化需从主臂内各个节臂长度出发,依据《汽车起重机设计规范》,结合汽车起重机起重性能确定主臂仰角参数[5]。在主臂长度确定情况下,规范工作幅度,确定回转中心到吊臂根部铰点的水平距离,通过分析主臂仰角,计算出吊钩中心离吊臂端部滑轮组中心连线与从根部铰点作与吊臂纵平行线的交点的垂直距离。当主臂变幅起升速度出现明显变化后,测量的液压变幅油缸驱动力也将发生变化,这种变化随着主臂长度增加而逐渐增加;当液压变幅油缸以相对匀速变幅运行时,主臂起升角度保持较小角度,能够保证主臂稳定运行;当主臂起升角度过大时,随着液压变幅油缸匀速运动,主臂运动无法保持匀速[6]。这种不匀速将使主臂变幅起升更为明显,再加上内部构建产生的冲击载荷,使得主臂安全性受到一定影响,为此在对主臂结构优化设计过程中,保持液压变幅油缸驱动力[7]。
1.2 汽车起重机转台优化
转台实体结构如图2所示。

图1 汽车起重机液压变幅机构模型简图

图2 转台实体结构
汽车起重机转台通常采用的是板式焊接结构,当转台受到分布载荷和节点载荷作用时,需将其以等效载荷形式转移到单元节点之中。根据转台不同板厚进行网格划分,保证转台受力均匀,使其能够承受平面内和法线方向的荷载。将转台的回转支承使用SOLID45进行网格划分,通过转台端点与立板间节点连接,能够减小局部应力,为液压变幅三铰点优化奠定基础[8]。
1.3 汽车起重机液压变幅三铰点优化
1)确定转台坐标系
由于在液压变幅过程中,不同组建变形量相对较小,因此,以各个组件为刚体,确定坐标系,如图3所示。
图3中a、b、c点表示吊臂与转台之间铰点、液压变幅油缸活塞杆与吊臂之间的铰点以及油缸缸筒和转台之间的铰点[9]。

图3 铰点位置坐标
2)约束处理
在进行液压变幅机构优化设计过程中,需将变幅动作中相对静止的零件固定,然后将上述确定的坐标系中a、b、c三个铰点连接,并在滑轮和吊臂之间创建铰接副,以此添加沿变幅油缸方向的平移变量[10]。
3)变幅三铰点优化布局
液压系统中负载决定了其压力的大小,而活塞杆的负载力则决定了整个变幅过程中的油缸压力。当液压系统压力减小时,说明活塞杆的最大与最小的承载力区间正在变小,此时汽车起重机液压变幅机构压力变化将会变小,而在整个液压过程中,变幅油缸活塞杆受力状况是与变幅三铰点布局方案有关的[11]。
利用ADAMS参数化功能将机构三铰点坐标值进行参数化处理,生成6个设计变量,当这6个变量确定时,液压缸长度和安装位置以及吊臂位置就被确定[12]。依据三铰点几何关系,综合考虑汽车起重机不同组件给铰点连接带来的影响,需确定6个设计变量取值范围,以变幅过程中最大值和最小值的差值为最优目标。三铰点位置优化后,说明原设计中的液压变幅油缸两个铰点位置会出现变化,随着油缸活塞杆承受变幅力波动变化,优化后的最大波动值减小,通过计算分析可知,优化后的汽车起重机仰角变化范围与原设计相比仰角变小了,起升高度和幅度变化也相对较小,工作性能得到提高。
由于吊臂铰点越靠近后台,就越有利于改善油缸受力状况,汽车起重机总体结构变量范围较小,因此,最优解只能在取值范围边界上,由此证实了单目标优化的局限性。为了提高汽车起重机工作效率,需采用复数矢量分析法进行液压变幅机构优化。
2 基于复数矢量分析法优化方案的实现
汽车起重机液压变幅机构按照工作性质可分为工作性变幅和非工作性变幅,其中工作性变幅主要用于起重机工作循环且带有负载条件情况下的变幅,该变幅时间对起重机生产效率具有一定影响;而非工作性变幅机构只能用于起重机空载状态下的幅度变化,以此调整装置作业位置,该工作方式对起重机生产效率影响较小。
2.1 复数矢量分析原理
复数矢量分析法是将机构看成一个封闭的矢量多边形,通过复数形式能够表示液压变幅机构封闭的矢量方程式,以此获取汽车起重机液压变幅机构模型直角坐标投影。
任意多边形能够用于多个三角形组合,机构方位图由多个三角形构成,三角形是运动分析的基础条件。采用矢量图解法分解三角形,如图4所示。
其中任何一个三角形都可以用矢量方程式来表示:

将三角形矢量方程式形式改为复数型:

矢量方程式中分别包含1l、l2、l33个矢量模态及3个相应幅角β1、β2、β3。只要给出其中1个参数,就可以得出其它未知的参数。未知参数的组合形式存在以下4种情况:
1)2个矢量方向及大小均为已知项,求解另1个矢量的大小与方向,由此获取唯一解,并编制子程序C1;
2)1个矢量的方向、大小为已知项,其余2个矢量仅已知其方向,求解另2个矢量的方向,由此编制子程序C2;
3)1个矢量的方向、大小为均为已知项,另一个矢量的大小及剩余矢量的方向为已知项,求取另外一个矢量方向和其余一个矢量大小,由此编制子程序C3;
4)1个矢量的方向、大小均为已知项,另一个矢量的大小为已知项,求解另一矢量的方向,由此编制子程序C4。根据矢量编制的子程序对机构受力情况展开分析。
2.2 液压变幅机构受力分析
为了降低驱动所耗费的功率,需改变工作性变幅机构,实现臂架的自重平衡。起重机液压变幅机构主要有三种布置方式,分别是前置式、后置式和后拉式,其主要特点如下所示:
1)前置式:采用小直径液压缸变幅推力较小,且臂下方有效空间较小;
2)后置式:将液压缸后移,需要的变幅推力较大,此时臂架受力不均;
3)后拉式:臂架前方有效空间较大。
随着主臂拉伸与回缩,液压变幅幅度也随之改变,但伸缩式臂架拉伸与回缩主要目的就是在起重机作业时,所伸出的臂架得到了较大幅度的起升,且在汽车行驶过程中收缩臂所获取的外形尺寸较小,通常不能作为机构使用。针对液压变幅机构受力分析如图5所示。
当液压变幅机构升起时,作用于转台上的作用力包括:吊臂根部铰支座拉力F1、油缸压力N、钢丝绳拉力F2、各个结构重力G1以及自身配重G2。依据各个结构受力情况,采用复数矢量分析法对机构进行优化设计。
2.3 优化设计
根据复数矢量分析原理以及各个结构受力情况,对汽车起重机液压变幅机构运动情况展开分析:在给定机构示意图下设计封闭矢量回路图,然后按照封闭矢量写出位置矢量方程式,并将位置方程对时间的按阶导数进行计算,通过上述四种情况,调整相应子程序,就可实现对汽车起重机液压变幅机构优化。

图4 矢量法图解三角形

图5 液压变幅机构受力简图
如图6所示,将其连接成五杆机构形式。
1)位置分析
通过封闭矢量回路写出矢量方程为:

复数表达式为:

通过调用两次编制子程序C1和C4,能够计算出β2和β3大小。
2)速度分析
依据位置分析结果求取一阶导数,得出速度方程,通过调用编制子程序C1和C2,求解出β2和β3方向。
3)加速度分析
依据速度分析结果求取一阶导数,得出加速度方程,通过调用编制子程序C1和C2,求解出其余角度大小和方向。
通过调用编制子程序,调节不同角度,能够保证液压变幅机构受力均匀,使汽车起重机各个组织结构受力和自身惯性大小成正比,对于不同组织结构,在任意外力作用下,都有可能会出现相同运动状态,通过对任意组织结构进行质量和惯性结合的时候,能够保证其在质量、质心和转动惯量矩方面保持一致性,由此优化汽车起重机液压变幅机构。
3 联合仿真及运动学分析
参考某企业汽车起重机液压变幅机构系统,对基于复数矢量分析的汽车起重机液压变幅机构优化设计方法进行联合仿真及运动学分析。
3.1 仿真参数设置
实验仿真参数设置如表1所示。

图6 五杆机构形式

表1 仿真参数设置

图7 臂架上仰运动过程中角位移曲线
3.2 俯仰运动学分析
1)角位移
分析臂架上仰运动过程中角位移曲线,如图7所示。
黑线表示的是联合仿真运动规律,蓝色表示的是复数矢量分析下的运动规律,绿色表示的是传统方法的运动规律。由图7可知,当时间为20 s时,传统方法下的角位移为30 °,而复数矢量分析下的角位移为12 °,联合仿真下的角位移为10 °;当时间为40 s时,传统方法下的角位移为38 °,而复数矢量分析下的角位移为25 °,联合仿真下的角位移为21 °;当时间为80 s时,传统方法下的角位移为55 °,而复数矢量分析下的角位移为47 °,联合仿真下的角位移为46 °。
复数矢量分析下的运动规律与联合仿真运动规律相一致,说明复数矢量分析方法的有效性及仿真正确性。但与此同时,两条线并不重合,说明存在一定差异,主要是因为两种理论并非完全相同。联合仿真运动规律是在实际运行状态下得到的,而复数矢量分析下的运动规律是经过理论分析获取的,因此存在一定差异。而传统方法缺少对汽车起重机液压变幅机构因素共同作用影响分析,导致其运动状态无法更加逼真接近实际值。
2)角速度
仰运动过程中角速度曲线,如图8所示。
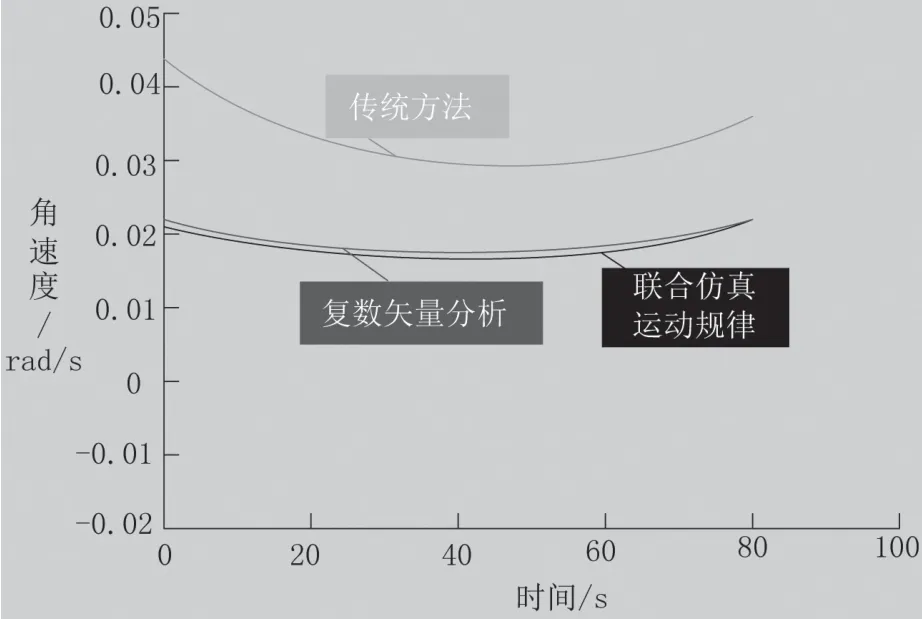
图8 仰运动过程中角速度曲线
汽车起重机液压变幅机构在80 s内去除掉开始和结束阶段,其他阶段角速度都是低于0.02 rad/s。由图8可知,当时间为20 s时,传统方法下的角速度为0.035,而复数矢量分析下的角速度为0.017,联合仿真下的角速度为0.016;当时间为40 s时,传统方法下的角速度为0.031,而复数矢量分析下的角速度为0.019,联合仿真下的角速度为0.018;当时间为80 s时,传统方法下的角速度为0.038,而复数矢量分析下的角速度为0.023,联合仿真下的角速度为0.023。
综上所述:采用传统方法角速度较快,与联合仿真运动规律相比明显偏大,而复数矢量分析下的角速度与联合仿真运动规律角速度基本一致,虽有偏差,但偏差较小,不影响优化结果。
3)角加速度
仰运动过程中角加速度曲线,如图9所示。

图9 角加速度曲线
在时间为80 s时,臂架上仰过程中的角加速度近似为水平线,视为匀速运动,角加速度数值保持在零值附近。受到联合仿真运动规律与理论仿真运动规律之间的差异影响,导致复数矢量分析与联合仿真运动规律曲线不同,尤其在终端时刻,两条线具有显著差异。产生这种现象的主要原因是在联合仿真中,俯仰角度闭环位置控制系统中的液压缸在预定重点位置附近做小幅运动,导致臂架角加速度震荡波动,属于正常波动数值,而传统方法波动数值并不在正常数值范围内。
4 结论与展望
4.1 结论
汽车其中以液压变幅机构现有研究主要集中在主臂、转台和三铰点位置优化方面,各个方面是相对独立的,无法形成一套有效联动机制。利用动力学仿真软件对变幅机构进行仿真研究,能够得出以下结论:
1)对于臂架上仰运动过程中角位移,采用传统方法缺少对汽车起重机液压变幅机构因素分析,导致其运动状态与联合仿真运动规律不一致。
2)对于臂架上仰运动过程中角速度,复数矢量分析下的角速度与联合仿真运动规律角速度基本一致,传统方法存在较大偏差。
3)对于臂架上仰运动过程中角加速度震荡波动数值并不在正常数值范围内,而复数矢量分析下的角加速度与联合仿真运动规律角加速度基本一致。
4.2 展望
对汽车起重机液压变幅机构进行全方位的动力学分析,能够获取基本数据信息,使得各部分数据得以应用,对于独立研究具有较大作用。但受到专业知识限制,所提出的研究项目需进一步深入完善,将具有类似属性的汽车起重机液压变幅机构整合,形成一套满足所有机构形式的有限元分析系统,具有一定应用价值。
