基于逆幂率模型的随机振动疲劳加速试验应用方法研究
2020-07-09曹强何亚屏王婷孙保涛刘斐
曹强,何亚屏,王婷,孙保涛,刘斐
(中车时代电气株洲变流技术国家工程研究中心有限公司,株洲 412001)
引言
在汽车、航天航空、轨道交通等行业中,外界环境的振动、冲击已成为影响产品稳定、可靠工作的关键因素之一,在产品设计、开发过程中需对振动疲劳耐久性进行充分的分析与评估[1]。对产品开展振动疲劳耐久性评估,一般需先采集、获取产品实际服役工况下的振动载荷谱,再借助振动疲劳耐久性快速评价技术,设计等效加速振动实验方案,从而在振动实验设备上快速完成其振动疲劳耐久性考核。通过准确、可靠的振动疲劳等效加速实验技术,可以快速评估出产品潜在故障与失效风险点,显著缩短产品开发周期,降低开发成本,提升产品竞争力。
目前工程实际应用中振动疲劳等效加速试验设计方法主要可分为幅值增强法和疲劳编辑法两类。幅值增强法基于逆幂律加速模型,保持谱型不变,等比例提高各频率点振动幅值,使得加速前后累积疲劳损伤一致,实现等效加速试验[2-4]。基于逆幂率模型的加速试验方法,由于加速设计方法相对简单、可执行性强,目前在国军标GJB 150.16A、汽车电气电子设备试验标准GB/T 28046.3(等同采用ISO 16750-3)、轨道交通GB/T 215639(等同采用IEC 61373)、美军标MIL-STD-810G等行业标准与工程实践中得到了广泛应用。疲劳编辑加速试验方法,首先采集结构危险位置的应变谱,通过雨流计数方法得到损伤时间历程曲线,然后基于损伤历程曲线对应变谱进行编辑处理,滤掉对结构损伤贡献较小的循环,最后借助重构技术生成用于加速试验的载荷谱[5,6]。损伤编辑法更加定量、精准化,但试验方法复杂、技术难度高。
基于逆幂律模型加速试验设计方法,在实际工程应用中还面临一个共性难题:如何确定合理的加速因子,以便尽可能缩短加速试验时间,而又能避免过度加速引起的过试验。目前对于加速因子的选择,还多依赖于经验和强化摸底试验,缺乏有效的指导设计方法。本文将基于加速试验前后疲劳破坏机理一致原则,结合结构服役工况下振动应力分析结果,研究提出一种加速因子上限值的计算方法,以提高实际工程应用中振动加速试验设计方案的准确性。
1 振动疲劳等效加速试验设计方法理论分析
1.1 随机振动疲劳加速试验模型
目前广泛采用的逆幂率加速模型关系式如下[2]:

式中:
Ts—实际服役工况下的设计寿命;
Tt—等效加速试验时间;
As—实际服役工况下的振动加速度均方根值;
At—等效加速试验条件下振动加速度均方根值;
Gs(f)—实际服役振动工况下的加速度功率谱密度;
Gt(f)—等效加速振动试验对应的加速度功率谱密度;
m—材料疲劳指数。
通常定义等效加速试验与实际服役工况下振动加速度均方根比值为加速因子α,即

由上述式(1)与式(2),则可以得到开展随机振动加速试验所需的加速等效时间与加速试验加速度功率谱密度:

由式(3)与式(4)可知,随机振动加速试验设计关键在于确定加速因子和材料疲劳指数m。
1.2 加速试验关键参数设计方法
1.2.1 服役设计寿命内振动循环次数修正计算
如图1所示,一般对于具有明显恒幅疲劳极限特性的材料,其S-N曲线根据应力循环破坏次数,分为低周疲劳破坏区间a-b、高周疲劳破坏区间b-c、无限寿命区间c-d。基于逆幂率模型的振动疲劳加速实验是基于材料疲劳曲线高周疲劳区间b-c段进行设计,当服役寿命内振动循环次数Ns大于疲劳极限转折点次数Nl时,加速试验实际是按图中b-c-d′曲线进行的加速,将导致过试验;当服役寿命内振动循环次数Ns大于恒幅疲劳极限点循环次数Nl时,结构若还没有产生疲劳破坏,则可认为结构可按理想无限疲劳寿命设计,用于加速计算的服役工况设计寿命内振动循环次数Ns需修正为Nl。目前轨道交通IEC 61373标准最新的2010版中进行加速试验设计时[7],如果计算出的服役寿命内振动循环次数超过108,需修正为108来进行加速试验量级计算。
服役工况设计寿命内振动循环次数Ns为:

式中:
按上述分析,为保证加速试验的等效性,当振动循环次数Ns大于等于恒幅疲劳极限点循环次数Nl时,需修正为Nl,即
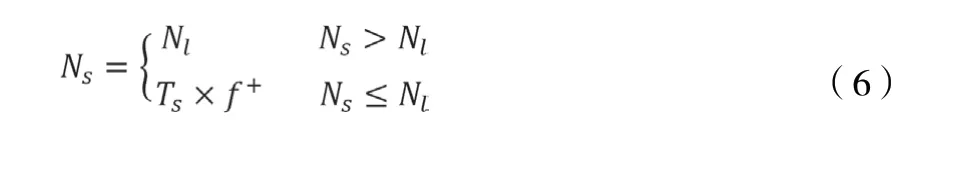
综合式(5)与式 (6),转换后可以得到用于加速试验设计的的服役工况设计寿命修正值Tsr为:

式(7)也可以表示为:

考虑一定的冗余,金属材料恒幅疲劳极限点循环次数Nl选取为108;平均振动频率可基于仿真分析结果,取节点应力功率密度谱的峰值穿越频率,或者由节点的1σ速度解除以1σ位移解得到[9]。
1.2.2 材料疲劳指数m
加速试验模型中材料疲劳指数m,主要取决于材料疲劳特性曲线(SbN=C)中的指数b,但同时也受材料表面质量、结构几何尺寸、平均应力、载荷类型等因素影响。对于随机振动加速试验,美军标MIL-STD-810G中建议材料疲劳指数m可取疲劳曲线指数b的80 %[8]。在实际工程应用中,由于产品往往包含多个不同部件,根据不同的材料疲劳曲线将设计得到不同的加速试验方案,因此需要综合统筹考虑产品材料组成、部件连接形式、应用领域可靠性要求。目前部分行业规范、标准与文献资料中,对于加速实验设计中疲劳参数m的取值规定如下:
国军标GJB 150.16A中对于随机振动,建议材料疲劳指数m取8[9];
美军标MIL-STD-810G中对于随机振动,建议材料疲劳指数m取7.5[8];
轨道交通IEC 61373标准中,建议材料参数m取4[7];
《振动与冲击手册》第五版中,指出对于金属的疲劳破坏,m取8对于大多数材料是合适的,然而在电气电子设备中对典型故障的机理一般取4较合适[10];
德国机械工程研究委员会制定的FKM标准中,对于母材正应力状态取5、剪切应力状态取8,对于焊缝正应力状态取3、剪切应力状态取5[11]。
综合上述,建议对于振动可靠性要求较高的一类产品或焊接结构类产品,建议取3~4;其他类型产品可参照材料疲劳曲线指数b的80 %,在5~8范围内选取。

图1 材料疲劳曲线示意图
1.2.3 极限加速因子计算方法
1)逆幂率加速模型只能考虑材料线弹性范围内的疲劳损伤等效行为,为保证加速试验疲劳机理不发生改变,加速试验不能处于如图1所示的低周疲劳破坏区间a-b(材料通常发生了塑性变形行为),而需位于高周疲劳区间b-c。
基于上述损伤等效准则,需保证加速试验振动循环次数Nt大于高低周疲劳转折点循环次数Np,即:

将式 (10)代入式 (3),可以推导得到加速因子α需满足:
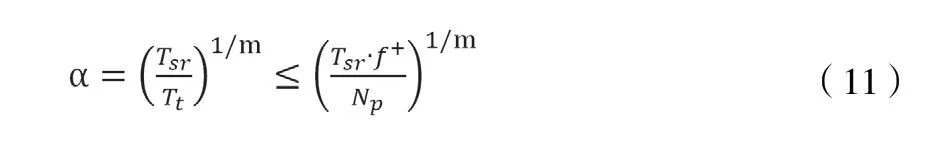
高低周疲劳转折点的循环次数一般为104。
2)为保证加速试验的等效,产品在加速试验前后的疲劳破坏机理不能发生改变。振动加速试验随着激励量级增大时,结构的承受的应力水平也随之增高,有可能超过材料屈服极限,而使得高周疲劳破坏转变为塑性变形引起的低周疲劳破坏。
随机振动加速前后振动加速度均方根值与振动应力水平成正比[3],即


图2 随机振动加速试验设计流程
式中:
σ1s和σ1t分别加速前后的产品结构危险位置的应力值。
基于Steinberg随机振动疲劳理论[12]:结构在随机载荷作用下的应力响应近似服从高斯分布,加速试验后结构在随机载荷下的最大应力水平σtmax可近似为3σ1t,即

为保证加速前后疲劳破坏机理的不变,加速试验后最大应力水平应不超过材料屈服强度σs,则有:

由式(12)与式(15)进而可以得到:

综合式(11)与式(16),可以得到极限加速因子αmax计算方法为:

结合式(3)与式(17)可以得到对应极限加速因子下最短加速时间Ttmin计算方法:

1.3 加速试验改进设计流程
综合上述1.1、1.2节提出的随机振动疲劳加速试验设计方法,可以制定如图3所示的随机振动加速试验改进设计流程。
2 加速试验实例分析
2.1 振动加速试验输入条件
选取某型号中央空调变频器装置为研究对象,分析产品在运输振动环境下产品可靠性。基于该装置运输振动实测数据,依据GJB/Z 126-1990中规定的统计容差法[13],归纳得到了如图3所示的运输振动载荷规范谱。运输里程按4 000 km考核,折算成运输时间约60 h。
2.2 加速试验关键参数计算
依据图3所示实测运输振动载荷谱工况,在Hypermesh和ANSYS建立了变频器装置随机振动有限元仿真模型,各方向随机振动应力求解分析结果如图4~6所示。

图3 变频器装置运输振动载荷规范谱
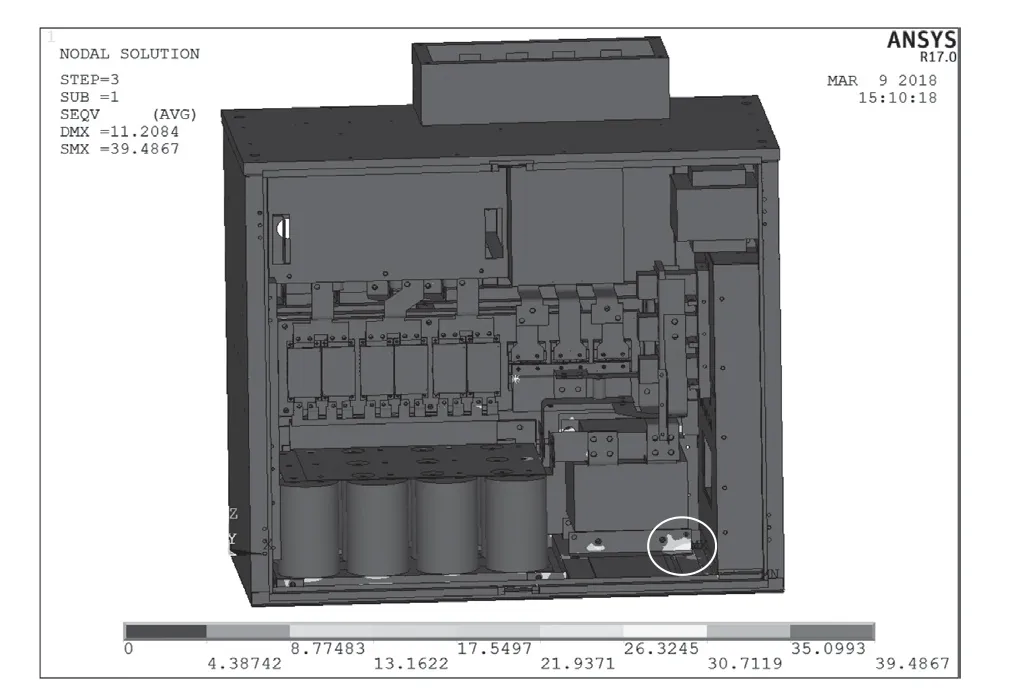
图4 实测运输载荷谱垂直方向随机振动1σ应力
提取每个振动方向最大1σ应力与平均振动频率,基于Steinberg振动疲劳计算模型[9],可以计算得到三个方向振动疲劳损伤值,并可以进一步按照前文1.2节所述方法计算加速试验关键参数,计算结果如表1所示。根据表1中各方向仿真分析与计算结果,横向所允许的振动加速程度最小,以此作为加速试验设计依据,将加速时间取整为4 h,相应可计算出对应的加速因子为1.72。
2.3 加速试验PSD谱计算
根据2.2节确定的各加速试验参数,由式(4)计算得到各方向用于加速试验的振动载荷谱,如图7所示。
2.4 加速等效试验

图5 实测运输载荷谱纵向随机振动1σ应力

图6 实测运输载荷谱横向随机振动1σ应力
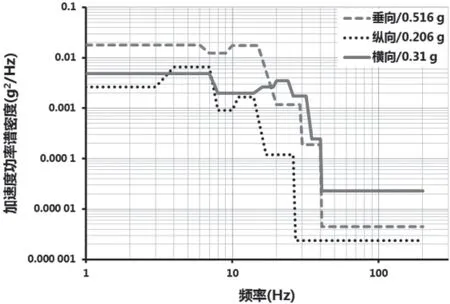
图7 运输加速振动试验载荷谱

图8 振动等效加速试验

表1 加速试验关键参数计算
基于上述2.3节计算得到的加速试验振动载荷谱,在振动台上依次开展变频器装置三个方向的振动等效加速试验(图8),试验完成后,产品外观和功能检查均无异常,与2.3节振动疲劳仿真分析结果吻合。进一步对比变频器装置内部IGBT模块横向振动响应的仿真与试验曲线,如图9所示,两者整体上较为吻合,尤其在50 Hz以下吻合度较高;一阶谐振频率、加速度均方根值仿真与试验误差如表2所示,两者误差均在5 %以内。基于仿真与试验对比分析结果,一定程度上验证了本文所述加速试验设计方法的可行性与有效性。

图9 变频器装置IGBT模块横向振动响应曲线

表2 变频器装置IGBT模块横向振动仿真与试验误差对比
3 结论
本文基于逆幂率加速模型,依据振动疲劳等效原则,通过理论分析与推导,确定了极限加速因子、材料疲劳指数、设计服役寿命等关键加速试验参数的计算方法,建立了随机振动加速试验改进设计方法与流程。主要研究结论如下:
1)对于具有明显恒幅疲劳特性的材料,当设计服役寿命内振动循环次数大于材料恒幅疲劳极限点循环次数时,用于加速试验计算的服役寿命内振动循环次数应按恒幅疲劳极限点所对应的循环次数进行修正计算,以避免可能导致的过加速。
2)逆幂率加速模型只能考虑材料线弹性范围内的疲劳损伤等效行为,为保证加速试验等效性,必须合理控制加速因子,不能使得振动疲劳由加速前的高周疲劳破坏转变为加速试验后的低周疲劳破坏,即需保证加速试验工况下结构最大应力水平不超过超过材料屈服强度。
