边坡预应力锚索服役寿命预测模型对比分析

2020-07-08王梓鉴

江西水利科技 2020年3期

杨俊，王梓鉴

（九江市水利电力规划设计院，江西九江 332000）

0 引言

预应力锚索在复杂的工作环境下，腐蚀问题非常严重，容易发生应力和腐蚀耦合作用下的应力腐蚀，最终趋于破坏，造成严重的工程加固失事后果[1]。在我国使用预应力锚索的50余年，出现了大量预应力锚索因腐蚀导致失效案例。如1976年采用预应力锚索加固的某桥台，5年后坍塌[2]；安徽梅山水库预应力锚索仅仅服役了6～8年就发生了断裂[3]；京珠高速公路粤境南段通车2年后就因锚索腐蚀失效发生滑坡[4]。因此，正确预测预应力锚索服役寿命对控制整个锚固工程风险具有重大工程价值。

目前关于腐蚀条件下预应力锚索服役寿命研究较少，破坏原因多种多样，腐蚀形式千变万化，预测服役寿命的关键在于是否能够有效确定其寿命达到终止的准则，不同的方法有不同的准则，预测的寿命也不同。目前常用锚索服役寿命预测模型有：锚索体受力达到屈服强度[4]、腐蚀锈胀量达到极限锈胀量[5]、氯离子入侵导致钢筋腐蚀[6]。李英勇[4]基于材料力学运用承载能力寿命理论以预应力锚索为主体，研究了锚索在长期应力作用下腐蚀作用导致锚索截面面积减小，承载能力降低，张拉力随之变化，从而使锚索体达到屈服强度造成锚索体破坏；邓东平等[7]基于弹性力学运用开裂寿命理论，研究了锚索注浆体在复杂运行环境下，注浆体由于钢绞线腐蚀作用锈胀开裂，进而加速腐蚀，导致锚索与注浆体之间的粘结力损失，最终锈胀量达到极限锈胀量导致锚索体从注浆体中脱落发生破坏；刘贞国[8]基于Fick第二定律运用电化学等知识，研究了氯盐和硫酸盐腐蚀环境下锚索服役寿命。3种服役寿命预测方法的研究对象不同，李英勇以锚索体破坏为主体，邓东平等着重于注浆体破坏，刘贞国以锚索工作环境为研究主体，3种模型的研究对象基本上涵盖了预应力锚索及锚索体本身，考虑的影响因素较全面，与实际工程接近。然而，这3种模型在预测预应力锚索服役寿命中的优缺点及适用性值得深入探讨。

本文首先介绍了3种腐蚀条件下锚索服役寿命预测模型的基本原理，然后系统比较了3种模型的优缺点和适用性，最后通过参数敏感性分析探讨了模型参数对锚索服役寿命的影响规律，从而为边坡预应力锚索加固设计和施工提供技术指导和参考。

1 腐蚀条件下预应力锚索服役寿命预测模型

1.1 模型一——李英勇模型

李英勇[4]根据材料力学，材料受拉力作用时，所受应力大于等于其屈服强度就意味着杆件失效，即：

式中：P为预应力锚索张拉力值，kN；A为锚索截面面积，mm2；σb锚索材料屈服强度，MPa。

众多学者研究表明[9～11]，预应力结构张拉力由于杆体材料松弛，岩体蠕变等因素影响，其量值由动态变化衰减直到逐渐趋于一个稳定的值。李英勇[4]根据工程现场长期实测资料，运用流变理论，考虑降雨变化、温度变化的影响，拟合得到适合工程实际的预应力锚索服役过程的时变张拉力计算公式如下：

式中：x1～x4为模型参数，可根据工程实测资料拟合确定；t为时间，月；△PTmax为温度变化引起的张拉力最大变化值，kN；△Pγmax为降雨引起的张拉力最大变化值，kN。

锚索因腐蚀作用，使得锚索应力大小不断变化，因此，确定预应力锚索腐蚀时变模型是计算锚索服役寿命的关键。李英勇[4]考虑钢绞线在pH值、时间、应力水平3个主要因素，进行了加速腐蚀试验，并结合工程现场实测数据拟合修正，得出腐蚀量时变计算公式：

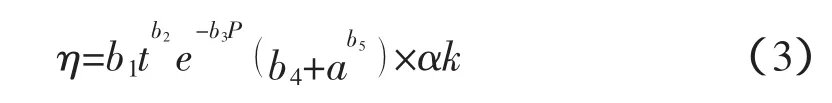
式中：η 是钢丝单位长度腐蚀量，g/cm；b1～b5为模型参数，可通过现场资料和室内加速实验拟合得到；t为时间，月；P 为 pH 值；a为应力水平，a=σ/σb，σ 为当前钢丝应力值，MPa，σb为钢绞线屈服强度，MPa；α 为锚索材料截面修正系数；k为腐蚀环境修正系数。假设钢绞线都发生均匀腐蚀作用，则钢绞线腐蚀后剩余的截面面积为：

式中：A1为钢绞线腐蚀作用后剩余截面面积，mm2；A为钢丝初始截面面积，mm2；ρ为钢丝单位长度质量，g/cm。将公式（2）、公式（3）和公式（4）代入公式（1）便可求得预应力锚索服役寿命t，为简便计，该模型称作“模型一”。

1.2 模型二——邓东平模型

由于施工过程中可能存在锚固段砂浆灌浆不密实，有空隙，使钢绞线发生锈蚀，邓东平等[7]在考虑注浆体外部围岩的约束作用和注浆体本身存在内部裂缝的情况下，根据弹性力学对注浆体进行受力分析得到极限锈胀力，再根据钢绞线、注浆体、外围岩体三者之间的变形协调关系得到极限锈胀力作用下的锚索锈胀量。其中，极限锈胀力计算公式为：

式中：ftk是注浆体的抗拉强度，MPa；qmax是极限锈胀力，kN；ζ是模型参数，计算公式为：

式中：c是保护层厚度，mm；d是锚索钢绞线直径，mm；注浆体泊松比 μb=0.15、0.2、0.3时参数 a1和 a2通过以下公式拟合得到：

式中：λ是注浆体外周的位移边界条件，当λ=0时，外围岩土体对锚固体形成固定约束，当λ=1时，无外围岩土体约束。极限锈胀力求出后，进而可求得锈胀量，计算公式如下：

式中：δ为锈胀量；Ec是注浆体弹性模量，GPa；Er为铁锈弹性模量，GPa，根据文献[12]，Er=6 000（1-2μr），其中 μr是铁锈泊松比，取 0.49；B、c1、c2是模型参数。参数B通过拟合而得：

当注浆体泊松比 μc=0.15、0.2、0.25 时，b1和 b2同样可由下式拟合得到：

c1和c2计算公式如下：

式中：n是体积膨胀率。结合工程实际可以获得锚索直径d，注浆体厚度c、弹性模量Ec、泊松比μc和抗拉强度ftk，因此，确定位移边界条件比例参数λ和锚索体积膨胀率n之后，就能得到极限锈胀力时的锚索锈蚀量，再选定合适锚索腐蚀率模型便可预测预应力锚索服役寿命，为简便计，该模型称作“模型二”。

1.3 模型三——刘贞国模型

预应力锚索大多处于含氯盐等腐蚀介质的水环境中，刘贞国[8]通过将服役寿命时间分割为氯盐腐蚀作用下的服役时间和供氧控制下的服役时间两部分。第1部分氯盐腐蚀作用下的服役时间为：

式中：t1为氯离子入侵到钢绞线表面的时间，月；β1为硫酸盐腐蚀后导致氯盐扩散系数增加引起的时间减小系数（0～1）；D 为氯离子扩散系数，m2/s；Ccr为氯离子临界浓度；Cs为水泥浆体表面处的氯离子浓度；c为水泥浆体保护层的厚度，m。按照美国寿命预测软件Life-365[13]，氯离子扩散系数D（m2/s）计算公式如下：

式中：w为注浆体水胶比。第2部分供氧控制下的服役时间为：

式中：βo为硫酸盐腐蚀后导致氧气扩散系数增加引起的时间减小系数（0～1）；βρ为硫酸盐腐蚀后钢绞线腐蚀率的增加引起的时间减小系数（0～1）；ρ为钢绞线腐蚀失重率钢绞线的线密度，g/m；d钢绞线的直径，m；T钢绞线的标准温度，一般按环境温度考虑，K；M为Fe的摩尔质量，等于56 g/mol；z为Fe的电极反应的电子计量数，取为2；F为法拉第常数，等于96 485；为氧气在整个保护层内的等效扩散系数，m2/s，计算公式如下[14]：

式中：w为注浆体水胶比；T为环境温度，℃；RH为环境相对湿度。两部分时间相加便是预应力锚索服役寿命时间，为简便计，该模型称作“模型三”。综上，可将以上3种模型的优缺点及适用性归纳如见表1所示。

2 工程应用

以山东某高速路堑公路边坡[4]为实例，对上述3种计算预应力锚索服役寿命的模型进行系统比较。该边坡采用预应力锚索进行加固边坡，使用500多根30～45 m长的锚索。5束7Φ5的高强度低松弛钢绞线为一孔预应力锚索，钢丝屈服强度为1 860 MPa，一束钢绞线截面面积为140 mm2，换算成直径为13.35 mm，每根钢丝线密度取1.554 2 g/m，单孔设计张拉力为850 kN。注浆体参考水电工程边坡常用预应力锚索参数[15]，注浆体抗压强度取40 MPa，抗拉强度取3 MPa，弹性模量取19.5 GPa，注浆体厚度取27.5 mm，水胶比0.45，泊松比为0.2。经工程现场监测，该边坡预应力锚索周围温度常年在12℃～14℃之间，对周围地下水，岩土体取样分析，得到pH=7.62，呈碱性。

2.1 采用模型一计算的服役寿命

李英勇[4]根据监测仪器长期监测结果进行拟合，得到 x1=5.578，x2=0.012，x3=219.66，x4=605.46，张拉力受温度变化影响变化值取多年变化平均值50 kN，张拉力受降雨变化影响变化值取多年变化平均值55 kN。同样根据室内加速试验和工程实际拟合得到b1=0.04399，b2=0.535 18，b3=0.250 47，b4=2.059 87，b5=3.740 76×10-3；锚索材料截面修正系数a=1；腐蚀环境修正系数k=1.24。文献[16，17]指出，由于预应力锚索是多束钢绞线、钢丝组成，张拉过程中存在不均匀性，极限荷载需要进行折减，即当锚索所受应力达到0.94σb时就认为已经破坏。计算时先将拟合出来的参数和实际工程情况的参数值代入公式（2）、（3），再将公式（3）的结果代入公式（4），得出变化之后的截面面积，最后将公式（2）、（4）的结果代入公式（1），看是否满足判别式，满足时的时间就是服役寿命；如果不满足将时间增大，继续代入公式，直至满足判别式（1），得到最终服役时间为31.8年，与李英勇计算结果33.3年基本吻合。

患者，男，30岁，因“劳累后下腰部正中及右侧髂腰部疼痛加重1年”就诊。追问病史，12年前新兵训练5 km武装越野时曾出现类似症状，疼痛视觉模拟量表（VAS）评分［2］5 ～ 7分，休息及对症治疗后症状消失；此后偶有劳累后腰痛，VAS评分2 ～ 4分，休息后减轻，未予重视，未行影像学检查。1年前更换岗位，弯腰负重增多，腰痛症状再次出现并进行性加重，VAS评分4 ～ 6分，且休息不能缓解。查体：腰部姿势僵硬，右侧腰部肌肉紧张；L4/L5棘突间隙触诊不清且有压痛，腰部屈伸时疼痛均加重，弯腰时痛点略下移；右侧L4/L5关节突关节处压痛，腰部前屈及向右侧侧曲时加重，VAS评分6分；下肢感觉、肌力正常。

表1 三种模型的比较

2.2 采用模型二计算的服役寿命

牛荻涛[18]将一般大气环境下快速锈蚀试验数据和大量工程检测结果的计算结果进行对比分析，根据各因素对钢筋锈蚀深度影响，拟合得到锚索锈蚀速率v（mm/a）：

式中：kcr是锚索位置修正参数；kce是环境条件修正参数，T是环境温度，℃；RH是环境湿度；c是锚索外围注浆体厚度，mm；fck注浆体抗压强度，MPa；考虑腐蚀速度在大气环境与预应力锚索工作环境的差异，根据文献[5]的建议取 kcr=1.0，kce=4.0，RH=100%。

引入折减系数ζ对室内加速试验腐蚀速率进行缩小：

本文取 ζ=0.2，将 T=13℃、c=27.5mm、σc=19.5GPa、kcr=1.0、kce=4.0、RH=100%，代入公式（16）、（17）计算得到锚杆（索）名义腐蚀速率。接着根据文献[7]计算极限锈胀量，λ 取 0.22，有 μc=0.2，代入公式（7）和（10），得出a1、a2、b1、b2的参数值，将 a1、a2、b1、b2分别代入公式（6）和（9）得到 A 和 B；将 c=27.50mm，d=13.35mm，ftk=3MPa和A代入公式（5）得到qmax。由铁锈膨胀率n=2，代入公式（11）得到c1和c2。由μr=0.49，根据Er=6 000（1-2μr）算得铁锈弹性模量。将计算出的参数qmax=13.71MPa、B=3.2104、c1=115.89×10-3、c2=0.03×10-3、Er=120MPa 和实际工程已知参数Ec、Er、d代入公式（8）得到极限锈胀力下的锈胀量。将极限锈胀力下的锈胀量δ除以名义腐蚀速度v*得到预应力锚索服役时间为31.2年。

2.3 采用模型三计算的服役寿命

根据文献[20]对氯离子扩散系数衰减指数的统计规律，由于实际工程中采用的是普通硅酸盐水泥，锚索处于含有水的环境下，氯离子扩散系数衰减系数均值为0.3，方差为0.05，因此，本文硫酸盐腐蚀后导致氯盐扩散系数增加引起的时间减小系数β，可参考氯离子扩散系数衰减系数取0.3计算。硫酸盐腐蚀后导致氧气扩散系数增加引起的时间减小系数βo与硫酸盐腐蚀后钢绞线腐蚀率的增加引起的时间减小系数βρ取0.3。根据文献[21]统计发现，氯离子临界浓度Ccr在1.24～3.08之间，本文取Ccr=1.7。根据文献[8]，注浆体表面处的氯离子浓度Cs取1.5。钢绞线腐蚀失重率取李英勇模型失效破坏时的腐蚀量对应的失重率。由注浆体水胶比和抗压强度，根据公式（13）、（15）得到氯离子扩散系数 D=7.94×10-12m2/s和氧气等效扩散系数，再将各参数代入公式（12）、（14），得到服役时间t=18.7年。

将3种预应力锚索服役寿命预测方法计算结果汇总，见表2。

表2 预应力锚索服役年限对比

由表2可知，采用模型一与模型二计算的预应力锚索服役年限较为接近，为33.3年和31.2年，模型三与前两者计算的预应力锚索服役年限相差较大，为18.7年。这是因为模型三假设处于深层内部岩土介质中的内锚段在供氧状态下，然而实际工程中预应力锚索被注浆体紧密包围，处于缺氧状态，供氧状态下的锚索腐蚀速率比缺氧状态下腐蚀速率要大的多，从而导致采用模型三计算的服役寿命偏小。因此，建议边坡预应力锚索服役31年后需要进行针对性的检测，对存在失稳风险的区域进行加固稳定。

2.4 参数敏感性分析

根据表1中总结的3种模型的主要参数进行参数敏感性分析探讨它们对预应力锚索服役寿命的影响，其中这些输入参数的参考值取值如下：锚索钢绞线直径取13.35 mm，每根钢丝线密度取1.554 2 g/m，注浆体抗压强度取40 MPa，抗拉强度取3.0 MPa，弹性模量取19.5 GPa，注浆体厚度取27.5 mm，水胶比0.45，泊松比为0.2。环境温度取13℃，PH为7.62，位移边界条件取0.22。

（1）探讨锚索直径d对锚索服役寿命的影响。d分别取 11mm、12mm、13mm、14mm、15mm、16mm，计算结果见图1。从图1可看出，模型一的服役寿命随着锚索直径d的增大而增大；模型二的服役寿命随着锚索直径d的增大而变小；模型三计算的锚索服役寿命几乎不受锚索直径d的影响。这是因为模型一只考虑锚索钢绞线直径d，未考虑注浆体厚度c，所以当锚索直径增大时，能承受的张拉力随之增大，服役寿命也随之增大。

图1 锚索钢绞线直径d对锚索服役寿命的影响

图2 注浆体厚度c对服役寿命的影响

（2）探讨注浆体厚度c对锚索服役寿命的影响。模型二与模型三考虑注浆体厚度c与锚索钢绞线直径d共同作用下的服役寿命，c取25.5～30.5 mm，锚索直径d取12～14 mm，如图2所示。由图2可知：当锚索直径d不变时，模型二与模型三的服役寿命随着注浆体厚度c的增大而增大；当注浆体厚度c不变时，锚索直径d增大将轻微缩减模型二的服役寿命，而模型三则不受影响。

（3）探讨环境温度T对锚索服役寿命的影响。采用模型二与模型三计算的服役寿命均受温度的影响，T取5～20℃研究，水胶比取 0.2、0.3、0.4，如图 3 所示。由图3可知，模型二计算的服役寿命在一定范围内随着温度的增加而减小，这是因为在一定范围内，温度的增加会导致腐蚀速度的加快；模型三的服役寿命，在水胶比等于0.2时，随着温度的增加而减小，但随着水胶比的增大，减小的值程度越来越小，当水胶比增加到0.4时，温度对模型三的服役寿命不起作用，当温度不变时，水胶比的增大会使锚索的服役寿命减小，这是由于在水胶比较低时，氯离子扩散系数较小[22]，腐蚀速度慢，这时候温度对腐蚀速度的影响较大一点，随之影响服役寿命，当水胶比较大时，氯离子扩散系数较大，腐蚀速度较快，温度对腐蚀速度的影响微乎其微，基本不影响服役寿命的大小。

（4）探讨钢丝线密度对锚索服役寿命的影响。采用模型一与模型三服役寿命受钢丝线密度的影响，钢丝线密度取1.1～1.7 g/cm，如图4所示。由图4可以看出，当钢丝的线密度增大时，模型一的服役寿命随之增大，且增大较多，模型三的服役寿命不受钢绞线密度变化的影响，数值基本不变，这是因为模型三在计算过程中，并没有考虑锚索体自身的因素，所以，当改变钢绞线密度时，不影响服役寿命。