LTE230MHz电力无线专网的频谱空洞感知技术
2020-07-08杨眉
杨 眉
(南方电网海南数字电网研究院有限公司,海口 570203)
0 引言
正交频分复用(OFDM)与频谱感知是LTE230系统的两项关键技术[1]。OFDM能够有效提高频谱效率和系统容量,同时还能抵抗多径干扰,是一种优秀的物理层传输技术[2]。针对OFDM信号的存在性检测属于二元检测问题,传统的算法主要有匹配滤波器检测、能量检测(energy detection,ED)、循环平稳性检测[3]。由于在实际环境中,待检测信号特征、噪声功率、信道特性等先验信息未知,所以基于协方差矩阵的盲频谱检测器应用更为广泛,如CAV检测器、MME检测器、BOC检测器等。
在频谱空洞检测方面,针对边缘检测问题,文献[4]提出了一种利用小波变换实现噪声功率估计,并根据噪声功率的估计进行能量检测的算法。文献[5]提出了基于能量检测的边界检测算法和单级尺度小波变换的频谱边界检测算法。能量检测算法复杂度较低,易于实现,但需要知道噪声方差,同时低信噪比(signal noise ratio,SNR)下性能较差;而单级尺度的小波分解边界检测算法对噪声十分敏感,导致检测性能不理想。文献[6]将该方法用于频谱空洞检测中,但只利用多级小波分解系数累积方法对频谱空洞检测进行了定性分析,同时该方法未考虑载波频偏对OFDM信号频谱和小波分解系数的影响,致使性能受限。
针对以上问题,为提高LTE230MHz电力无线专网频谱利用率,本文提出了一种存在载波频偏的OFDM系统频谱空洞感知技术。首先构建接收信号协方差矩阵,通过最小化其非对角线元素的能量,估计并消除载波频偏;然后对其对角线元素序列进行多尺度小波变换,寻找序列的边界奇异点,即OFDM符号频谱的边界点,完成频谱空洞检测。
1 系统模型
本文以LTE230MHz电力无线专网为研究背景。假定活跃用户采用NC-OFDM的传输方式使用频谱资源,分别占用一段连续的子载波,即频谱块。不同用户的频谱块之间没有交叠,并且在用户频谱间存在保护间隔。本文将正在使用频谱资源的用户称为活跃用户,进行频谱感知的用户称为认知用户,未被占用的频段称为频谱空洞。
针对LTE230MHz电力无线专网的应用场景,NC-OFDM通信系统频谱感知主要包含两个过程(如图1所示):①活跃用户是否存在;②如果有活跃用户存在,其频谱占用情况(位置及功率)如何。其中,第一个问题属于活跃用户存在性检测,为粗检测;第二个问题为功率谱密度边界检测及功率估计,为精检测。
活跃用户存在性检测用以判断信号的有无,边界检测为定位频谱空洞位置。由于基于协方差矩阵的感知算法具有感知性能好、不需要先验信息等优点,本文假设已通过该类算法完成频谱存在性检测(图1虚线框部分)。针对存在信号条件下的OFDM频谱边界检测问题(图1实线框部分),提出了一种改进的OFDM系统频谱空洞检测算法。
为不失一般性,采用通用的OFDM传输模型,第k个OFDM调制块可以写成
b(k)=FNa(k)
(1)
接收到的OFDM信号,在去除CP后的时域信号可以表示为[7]
(2)

(3)
(4)
(5)
式中diag[*]表示取对角元素运算。
考虑感知频段为[f0,f1],总带宽为BMHz,存在的活跃用户总个数为U。频谱空洞的检测需要在待感知频段上寻找U个活跃用户频谱块的边界集合Ω={(S1,E1),…,(Su,Eu),…,(SU,EU)},满足条件f0≤Su (6) 由文献[8],式(5)可以写为 (7) (8) 式中Hl为第l个子载波上的信道频率响应。由式(7)可以看出,当存在载波频偏时,由于载波频偏破坏了子载波之间的正交性,接收信号的功率谱被衰减Il-k(ε)Hl,使得信号功率谱P(k)在频带内起伏变大,带外衰减变慢。频偏越大,该现象越明显,如图2所示(仿真条件:高斯信道,SNR为10 dB,N=64,其中第16到48的子载波设置为空载波,QPSK调制)。从图中可以发现,频偏使得空载波处的功率谱密度提升,同时减小了数据子载波处的功率谱密度。 当存在载波频偏时,文献[5]直接采用能量检测法或小波变换法提取功率谱边界。但由于载波频偏容易造成功率谱带内起伏,直接检测边界容易产生虚假边界,从而导致检测出虚假空洞;同时,载波频偏还会造成功率谱带外衰减变慢,直接提取时容易使得检测出的频谱空洞边界位置偏离真实位置,使得频谱边界归一化均方误差(NMSE)变大。 继续化简式(4),可以得到 (9) (10) (11) 式中:⊙表示Hadamard积;IIN为N阶全1矩阵。 (12) (13) (14) (15) 通过式(15)求解载波频偏,然后进行频偏补偿和DFT后,由式(5)得到信号功率谱密度。实际情况中P(k)可以通过保存求解频偏的中间结果Q(v0)、Q(v1)的对角线元素获得。 小波变换具有良好的降噪特性,已广泛应用于信号和图像的边缘检测中[9]。本文算法通过对频偏补偿后的信号功率谱密度进行多尺度小波变换,分析多尺度小波系数累积函数的奇异点来识别各活跃用户占据的频带边缘,从而完成频谱空洞检测。设u(f)为小波平滑函数,θ(f)=d[u(f)]/df为小波母函数,θ(k)为θ(f)在其支撑区间上离散化后的小波函数,令θs(k)=θ(k/s)/s,尺度因子s=2m(m=1,2,…,M),M为小波变化的级数,则功率谱密度P(k)的连续小波变换(continuous wavelet transform,CWT)Ws(f)及其一阶导数可以分别表示为 WS(k)=P(k)×θS(k) (16) (17) 本文选用具有良好降噪特性的高斯函数作为小波平滑函数,采用三级尺度小波变换的累积检测信号边缘,代价函数为 (18) 分析可知三级尺度小波变换累积函数的极大值点对应于活跃用户起始边界,极小值点对应于活跃用户结束边界。 小波去噪另一个关键点是门限的选取。文献[10]采用Donoho提出的VisuShrink方法[11],但该方法在小波变换系数长度L较大时,存在严重的“过扼杀”现象[12]。由于小波变换并不改变高斯白噪声的统计特性,根据高斯分布中的3σ原则,本文选取的阈值为[13] Th=3·median(|D(k)|)/0.675 (19) 则活跃用户的起始频点和结束频点为满足阈值条件的极值点,可以表示为 (20) (21) 当不存在干扰时,活跃用户的起始频点和结束频点交替出现;当干扰存在时,干扰可能造成D(k)产生额外的局部奇异点。因此实际中可以将式(20)和(21)中求取连续出现的多个Si中的最大值或Ei的最小值分别作为实际活跃用户的起始频点和结束频点。 综上所述,本文提出的基于协方差矩阵的多尺度小波变换频谱空洞感知步骤如下: 1)首先计算接收信号rs(k)的协方差矩阵cov(rs(k))。 为验证本文所提算法,下面给出计算机数值仿真结果。仿真环境包括3个LTE230活跃用户和1个认知用户。采用的OFDM系统如下:子载波数目N=256,CP长度NCP=16,调制方式为QPSK,观测的OFDM符号个数M=40,频偏在(0,1)内随机分布。作为性能比较,仿真加入能量检测和文献[5]的算法。在ED检测法中假设已知噪声方差,当存在噪声不确定度时,用p表示噪声不确定度的大小。假设3个LTE230MHz活跃用户的频谱边界定义为Ω={(15,30),…,(71,136),…,(200,237)},即活跃用户分别占用[15:30]、[71:136]、[200:237]三个区间;边界矩阵MU=[15 30;71 136;200 237]。所有结果采用10 000次蒙特卡洛仿真得到,仿真信道为高斯信道;频谱边界检测的性能由频谱块个数同时检测概率Pd(当检测到的活跃用户个数与设定个数相同时,认为成功检测,否则检测失败),定义边界NMSE为 (22) 不同算法的频谱空洞检测概率如图3所示。从图中可以看出,当信噪比较低时,能量检测法的检测性能主要受虚警概率(probability of false alarm,Pfa)影响。设定的Pfa越高,ED检测的检测性能越好。但当Pfa大于等于10e-1时,检测概率将会出现98%左右的检测平台。当信噪比满足大于等于-4 dB时,Pfa为10e-3条件下的ED检测法的检测概率与本文算法相当;但当信噪比满足小于-4 dB时,本文算法远优于ED检测算法。同时,当考虑噪声不确定度时,本文算法的检测概率优于Pfa为10e-3且噪声不确定度大于等于1 dB时的ED检测。另一方面,可以看出本文算法较文献[5]采用的方法,无论是高信噪比还是低信噪比均有1 dB左右的性能提升。 图4、5为本文算法与ED算法的NMSE对比。从图中可以看出,低信噪条件下,本文算法远优于ED检测算法;当信噪比处于-5~-2 dB之间时,本文算法略差于ED检测算法;同时从图6可以发现,本文算法无论是高信噪比还是低信噪比下均优于文献[5]的检测算法。当信噪比较高时,由图4可以看出,3种算法的NMSE性能均出现平台,本文算法与文献[5]以及不考虑噪声不确定性条件下,Pfa为10e-3时的ED检测算法的检测平台相当。由图5可以看出,当考虑噪声不确定度时,本文算法相较于ED检测法具有更低的误差平台。 从仿真结果可以看出,当信噪比较低时,检测概率主要受噪声和频偏等因素的影响。由于小波变换具有良好的抑制噪声特性,因此基于小波变换的检测方法优于ED检测法。而当信噪比较高的时候,ED检测法的边界归一化均方误差平台主要受频偏等因素的影响,平台大小随虚警概率和噪声不确定度p的减小而减小;而对于本文算法和文献[5]采用的算法,影响边界位置平均误差的关键原因不再是频偏,而是小波变换法本身对信号功率谱的平滑处理。 为了适应我国智能电网的快速发展,亟需提高230 MHz频段的使用效率,以承载更高速率和质量要求的业务。基于认知无线电的频谱共享正是一种有效的解决方案。为此,本文提出了一种面向LTE230MHz电力无线专网的频谱空洞感知算法。在基于协方差矩阵的活跃用户OFDM信号检测的基础上,利用载波频偏估计和补偿以及小波变换实现存在载波频偏条件下的频谱空洞检测方法。该方法首先根据接收信号协方差矩阵的对角化准则,求取并补偿载波频偏,然后对补偿后信号的功率谱进行多尺度小波分解,通过对求取的多级小波分解系数累积函数的奇异点来完成活跃用户的频谱边界检测,从而完成频谱空洞感知。仿真结果表明,该算法较已有的算法不需要先验信息,并且检测概率和边界归一化均方误差均有一定程度的改善。2 改进的频谱空洞检测算法
2.1 频偏对信号功率谱边界的影响
2.2 基于协方差矩阵对角化准则的频偏估计算法

2.3 基于多尺度小波变换的频谱空洞检测算法
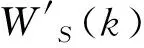

2.4 复杂度分析
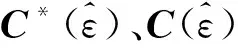


3 仿真分析
4 结束语
