带时间窗的多式联运路径优化模型及算法研究
2020-07-07杨楠
杨楠
(中国铁路兰州局集团有限公司科技和信息化部,甘肃兰州730000)
1 引言
多式联运作为一种高效的货物运输组织形式,具有整合不同运输方式的优势,通过有效转换和无缝衔接来提高货运效率和质量。在集装箱多式联运网络中存在若干个运输节点和多种运输方式,如何合理地做出各种运输组织与调度的决策是提高联运效率的关键,这些决策尤其体现在运输方式选择与运输路径组合优化方面。
张运河等[1]对运输费用和中转费用进行分析估计,得出广义费用最小的运输方案,并利用Dijkstra进行求解。Chang等[2]考虑了固定运输成本、运输中转成本,以此构建了以最小成本为目标并带有时间窗的规划模型。刘舰等[3]考虑了运输成本、运输的时效性,以此建立了基于运输成本最小的综合优化模型。张建勇[4]具体描述了多式联运网络,并以总成本最小为目标,建立了一种多式联运网络的最优分配模型。孙华灿等人[5]提出了多种运输方式联合的合理运输路径,考虑运输过程中运输方式序列的合理性以及转运次数的合理性,建立了以运输费用最低为目标的联合运输合理路径选择模型。张家应等人[6]考虑军事运输的特殊性,战时要求时最短,平时要求总成本最低,分别以运输时间最短和总成本最小为目标建立模型,在计算时间、费用时,考虑了超出运输期限造成的时间和成本的损耗。雷英杰等人[7-8]提出采用Matlab的遗传算法工具箱来求解该复杂问题,并通过案例予说明,将铁、水、公、空等运输方式的道路网络直接用于求解,但传统遗传算法的运行效率十分低。杨秋秋[9]将多式联运的运输优化问题转化为最短路径问题,使用遗传算法来求解该问题。此种方法适用于网络较小的情况,而且在实际中时间最短未必总成本最少,该遗传算法有待改进。
在已有求解过程中,多是采用传统的遗传算法或者确定性的最短路求解问题,没有考虑时间与总成本的联系分开求解。结合各种运输方式的客观需要,本文以总成本最小为目标建立模型,考虑了运到时限因素,在总成本中加入超过约束时间的惩罚成本,同时采用一种基于floyd的K短路算法并结合遗传算法为各路段分配合理的运输方式,从而指导运输方案的制定。
2 多式联运模型构建
2.1 问题描述
现有一批货物,欲从O点送至D点,运输途中有n个节点(城市),任意相邻节点之间均有k(k=1,2)种运输方式,每个节点都可以转换货物的运输方式,转运需一定的中转费用和中转时间,构建从出发点到目的点的完整路径,选择OD间最佳的运输方式和运输路径组合,以使总成本(包括运输费用和时间成本)最低,且尽可能满足托运人的运到时限。
2.2 模型假设
①货物在运输节点中不可分开运输;②货物的转运只能发生在节点,且在各节点最多进行一次转载;③货物在两个节点中只能选择一条运输路径和一种运输方式;④货物在节点即时转运,没有库存[10]。
2.3 符号说明
构造网络G(V,E),其中V为节点集合,E为节点间的弧集;L为运输方式集合;为从节点i到节点j选择第k种运输方式;表示在i点运输方式由k转换为l;为从节点i到节点j选择第k种运输方式时所需的费用;为在节点i处,运输方式由k转换为运输方式l时所需要的费用;Tmax、Tmin分别为运到时限的上、下界;p表示实际运输时间低于下限的惩罚因子;q表示实际运输时间高于上限的惩罚因子;为在节点i、j之间以第k种运输方式通过时所需的时间,其由和分别为通过节点i到j的距离与所选运输方式的速度[11-12]。
2.4 模型建立
根据以上描述,模型可被定义为具有时间约束的路径及运输方式选择问题,其目标为在使总成本最少的前提下,尽可能满足托运人的时间需求,可建立如下模型[13]:
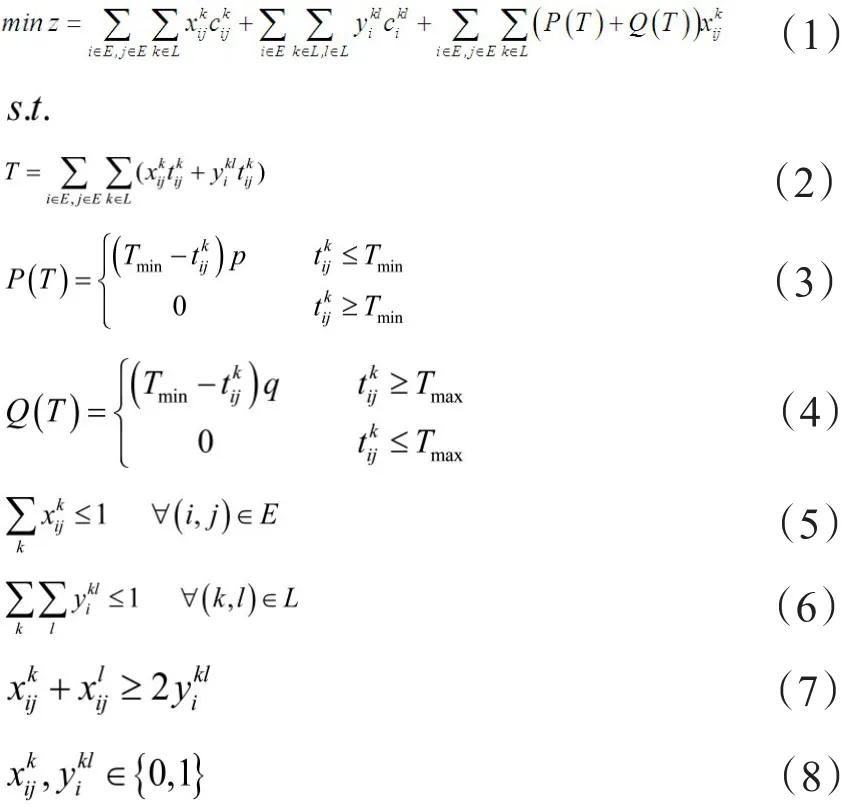
上述模型中,目标函数(1)表示总费用最小,其主要包括三部分:运输成本运输方式转换成本,超出限制时间的惩罚成本;约束(2)表示整体运输时间为各节点间运输时间与转运时间之和;(3)和(4)分别表示运到时间超出时间约束的下限惩罚函数和上限惩罚函数;(5)和(6)表示任意两节点间只采用一种交通方式,任意节点处最多进行一次运输方式转换;(7)确保运输的连续性;(8)决策变量为整数。
3 算法设计
本文研究的问题属于网络优化问题,而网络和路径优化本身就属于组合优化的问题,该问题已经被吕凯等[14]证明是NP-hard问题。目前已有相当多的文献提出了求解该类问题的方法,并且随着计算机技术的不断应用,用于解决此类问题的新方法也不断涌现,具体可以归纳为两大类:确定性算法和启发式算法。结合确定性算法和启发式算法的特点及其适用范围,对本文所要求解的问题分两个阶段进行求解,第一阶段利用基于floyd的K短路算法求出K条运输路径;第二阶段利用遗传算法,为求出的K条运输路径分配运输方式。
3.1 基于Floyd的K短路算法
本文研究的路径优化问题中,两点间的弧无方向约束,即运输网络为无向图。在多式联运中,所求的最短路并不一定是运输网络中的最优方案路径,基于此,将求出的K条最短路作为初始方案中的路径。具体步骤如下:
对于每一对顶点i和j,看是否存在一个顶点w使得从i到w再到j比已知的路径更短,如果是更新它;把网络图G用邻接矩阵表示,如果从i到j可达的路径,则G[i,j]=d,d表示该条路径的长度,否则G[i,j]=无穷大;定义一个矩阵D用来记录所插入点的信息,D[i,j]表示从i到j需要经过的点,初始化D[i,j]=j;把各个顶点插入图中,比较插点后的距离与原来的距离,G[i,j]=min(G[i,j],G[i,k]+G[k,j]),如果G[i,j]的值变小,则D[i,j]=k;G中包含两点之间最短道路的信息,D中则包含了最短可通过路径的信息。
3.2 遗传算法
遗传算法采用概率的变迁规则来指导搜索方向。因此第二阶段将上述所求得的K条短路作为问题的初始可行路径,利用遗传算法为其匹配运输方式。
3.2.1 染色体编码和种群初始化
在运输网络中,用V={1,2,3L n}表示城市节点集合,用L={1,2}表示两种运输方式[11](公路、铁路)。以第一阶段所求出的K条最短路进行循环,随机取L中元素,插入到方案路径中,即为各个路段分配了对应的运输方式,从而形成了有K条染色体的初始种群,染色体编码如图1所示。在编码过程中,城市节点和运输方式分别进行编码,图中城市编号中的0表示不通过该节点。
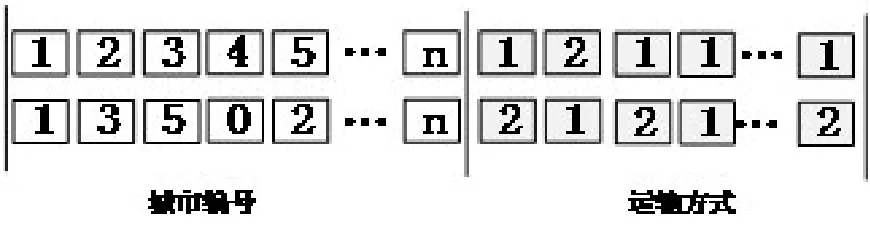
图1 染色体编码图
3.2.2 适应度函数
本多式联运问题将目标函数的倒数作为适应度函数[15],适应度函数为
3.2.3 选择算子
选择操作主要分为两个阶段:第一是计算出单个个体的适应度值;第二是以轮盘赌选择法来进行个体的选择,具体的操作过程如下:
3.2.4 交叉算子
交叉算子可以产生新的个体,采用双点交叉,在城市节点和运输方式中分别随机产生两个交叉点,把两个交叉点之间的基因进行交换,得到新的个体,具体的交叉过程如图2所示,虚线位置表示随机选择的交叉点。
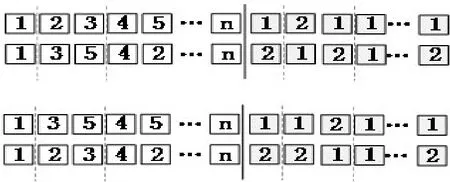
图2 双点交叉算子
3.2.5 变异算子
变异算子是指将个体编码串中的某些基因值改变或者替换成其他的基因值,从而形成一个新的个体。遗传算法中使用变异算子的目的主要有两个:一是改善遗传算法的局部搜索能力;二是维持种群的基因多样性,抑制早熟。本文变异采用双点变异,具体的变异方式如图3所示。

图3 双点变异算子
3.3 算法流程
Step 1.设置算法初始值;
Step 2.利用floyd算法,找出初始最短路;
Step 3.删去原值中最短路的边的权值,从新的权值矩阵中求出新的最短路,即次短路,顺次求出N最短路,即最初方案;
Step 4.编码,对上述N最短路进行循环,随机产生小于等于k的正整数,插入最短路方案中,即为各个路段分配了对应的运输方式,从而形成一个完整的染色体;
Step 5.初始化,根据step4产生初始种群并计算适应度值;
Step 6.对Step5的结果进行轮盘赌选择;
Step 7.将选择出来的染色体两两进行交叉;
Step 8.检查生成路径是否可行,如果可行,保留个体;如果不可行,将父代的两条染色体执行Step 9;
Step 9.变异操作,返回Step8;
Step 10.终止条件,若连续若干代的最优解相同,则终止迭代,解码并输出最优个体与目标函数值。
4 案例设计
现在有一批50 t货物从节点1运送到节点18,如图4,整个运输过程中共有公路,铁路,两种运输方式可供选择,各节点间运输距离如表1,各运输方式特征如表2,算法初始值见表3。现要求在托运人指定的时间窗[18 h,24 h]内,用最小的经济成本,选择合理的路径和运输方式搭配,将货物从起点运至终点。其中公铁单位换装费用为10¥/t,单位换装时间为0.01 h/t。
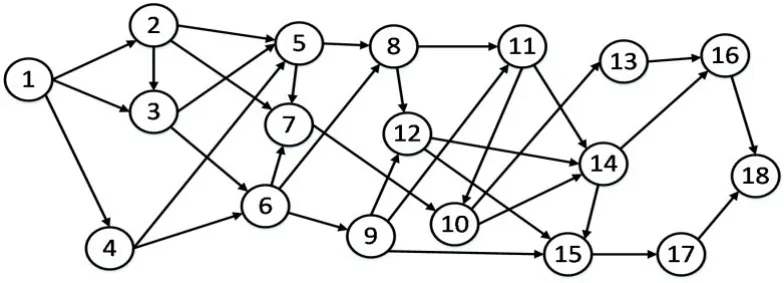
图4 城市节点连接图
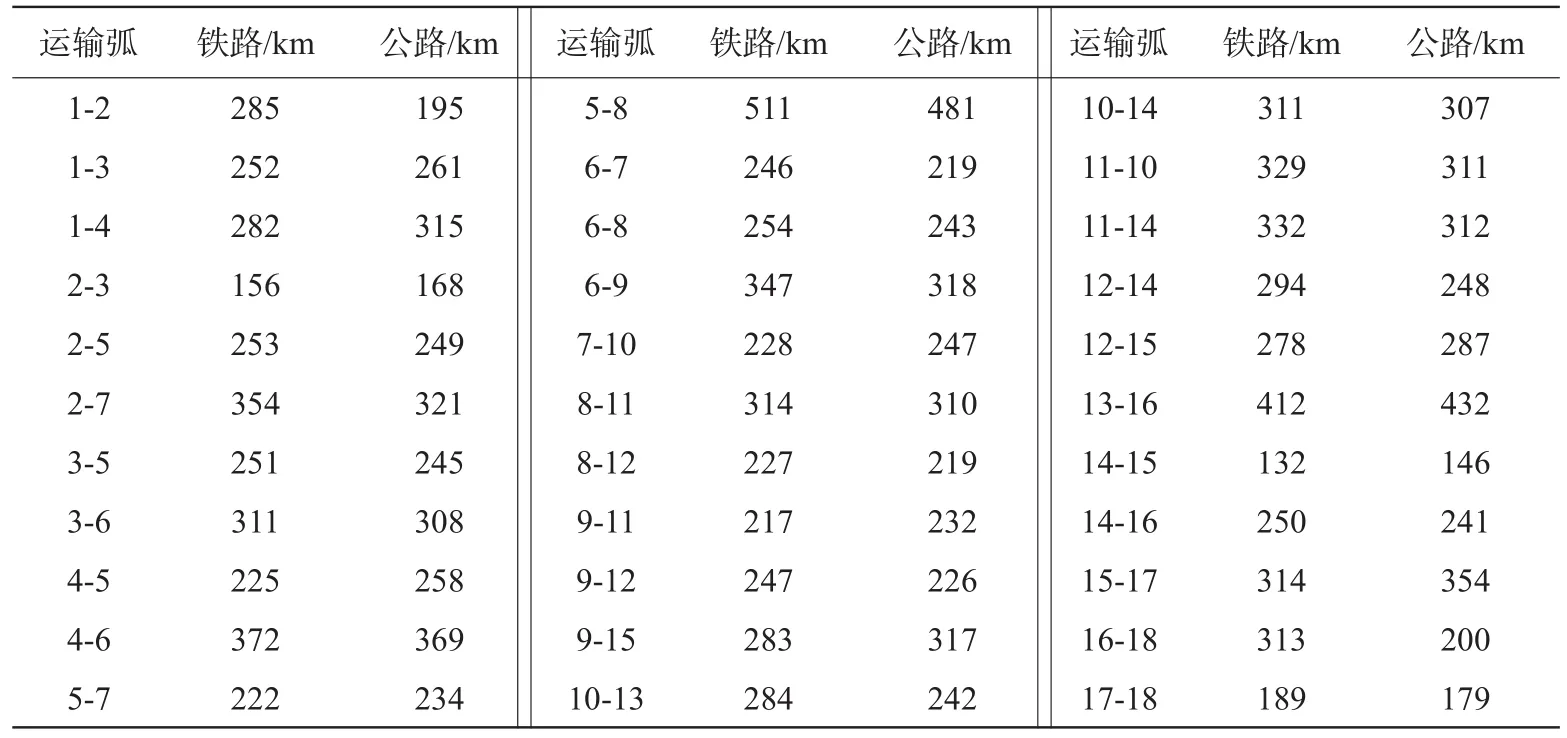
表1 节点间运输距离
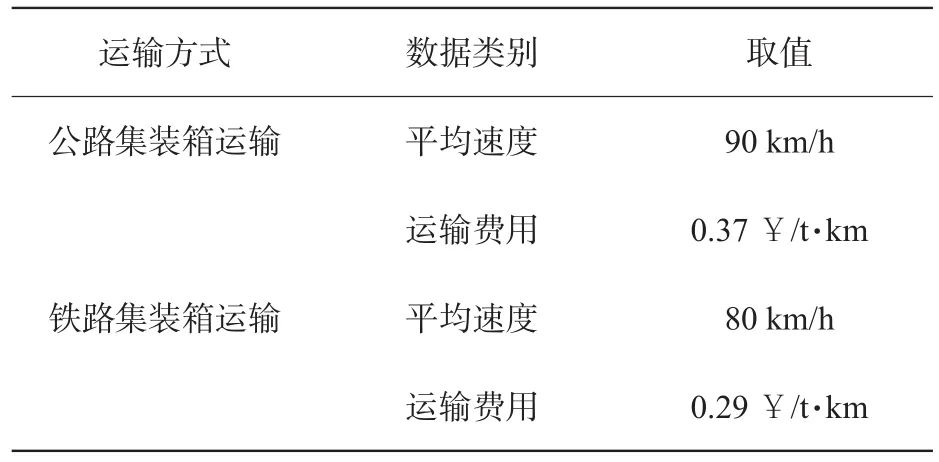
表2 运输方式特征
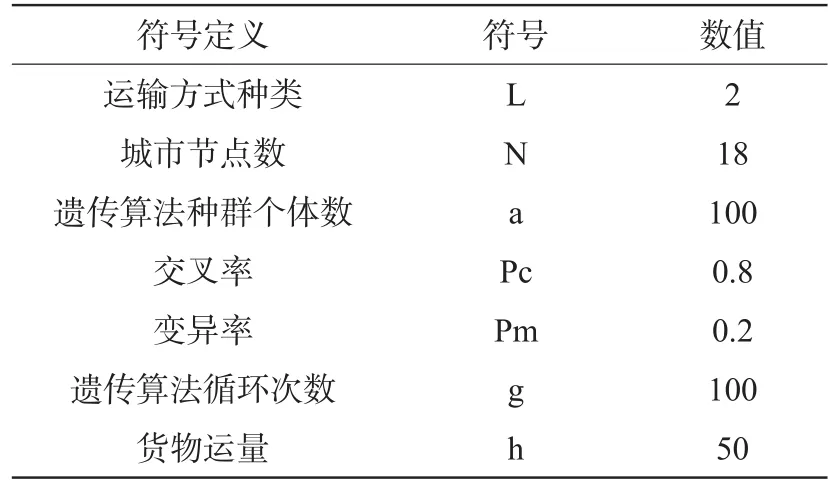
表3 算法初始值
本算法属于启发式算法,收敛结果具有一定随机性,为验证混合算法的普适性,在此取各算法运行10次中的最好解和性能评价指标进行对比。
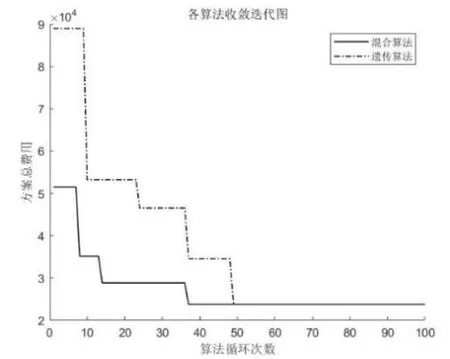
图5 各算法收敛图

图6 算法结果
以此算例作为测试集,运行结果如图5~6所示,表4给出了两种算法的求解结果,由结果可知,各算法求得最佳路径均为1→2→7→10→14→16→18,其中转运方式为:公→铁→铁→铁→铁→铁,总花费为23 755元,该方案总耗时19.604 2 h。

表4 各算法求解结果
从结果可知混合算法能够有效收敛到最好解,且收敛代数较传统遗传算法减少22.9%;从仿真过程可以看出混合算法具有更快的收敛能力和更好的优化性能。
5 结语
通过对多式联运和遗传算法相关的大量文献进行研究,在对运输方式和运输路径合理选择的基础上,考虑运输成本、转运成本、时间惩罚成本建立了多式联运网络优化模型。
设计了基于floyd的K短路-GA混合算法,该混合算法增强了算法的搜索能力,避免出现局部最优解,并利用MATLAB对模型进行仿真计算,能够求解得到总成本最少的联运方案。
将该混合算法和传统遗传算法同时应用于多式联运算例求解,从混合算法的传统遗传算法的求解结果对比可知混合算法在约36次迭代时达到最优,传统遗传算法到约50次迭代才达到最优,表明混合遗传算法较传统算法收敛更快,并验证了混合算法的有效性。
