线性离散时间系统的有限时间镇定

郁鹏飞，傅 勤

(苏州科技大学 数理学院，江苏 苏州 215009)

引言

在控制领域中, 有两类不同的有限时间稳定性的概念. 第一类引出背景是出自于Dorato在1961年提出的短时间稳定性(Short time stability)[1], 这类稳定性有别于通常意义下的Lyapunov稳定性, 考虑的是在二次性能指标下, 从初始时刻起的某一有限时间段内, 系统状态的二次性能指标是否小于初始状态的相应量[2-4]; 第二类引出背景是出自于通常意义下的Lyapunov稳定性, 考虑的是系统是否满足Lyapunov稳定性, 并且状态变量能否在有限时间收敛至平衡点[5-11]. 本文研讨的有限时间稳定性为上述第二类.迄今为止, 涉及这类有限时间稳定性的研究工作针对的均为连续时间系统[5-11].如何将有限时间稳定性等相关概念引入到离散时间系统中, 并进行相应的有限时间控制设计，据笔者所知, 尚无相关的研究论文.

本文提出的离散时间系统有限时间控制问题, 是先将有限时间稳定、镇定等相关概念引入到离散时间系统中, 然后针对一类线性离散时间系统进行有限时间控制设计, 构建得到状态反馈控制律.借助于矩阵运算, 证明当反馈控制律作用于该系统时, 闭环系统是有限时间稳定的.

1 问题描述

由参考文献[5-11], 对离散时间系统, 给出相应的定义如下:

定义1 称离散时间系统x(t+1)=f(x(t)),x(t)Rn是有限时间稳定的, 是指系统满足Lyapunov稳定性, 且可在有限时间收敛至平衡点,t=0,1,2.

定义2 称离散时间系统x(t+1)=f(x(t),u(t)),x(t)Rn,u(t)Rm, 是基于状态反馈有限时间镇定的, 若存在状态反馈控制律u(t)=φ(x(t)), 则使得闭环系统x(t+1)=f(x(t),φ(x(t)))是有限时间稳定的, 其中t=0,1,2….

考虑如下形式的线性离散时间系统:

x(t+1)=Ax(t)+Bu(t),x(0)=x0

(1)

这里x(t)Rn,u(t)Rm分别是系统的状态和控制输入,t=0,1,2… .

有限时间镇定的目的是寻找适当的状态反馈控制律u(t)=-Kx(t), 使得闭环系统x(t+1)=(A-BK)x(t)是Lyapunov稳定的, 且存在某个正整数N, 使得x(N)=0,t=0,1,2,….

2 主要结论

对式(1)给出如下假设条件：

假设1 (A，B)是完全能控的.

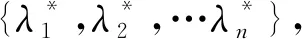
(2)

由此可引出本文的主要结论:

定理1 若假设1成立, 则存在状态反馈矩阵K, 使得闭环系统：

x(t+1)=(A-BK)x(t)

(3)

是有限时间稳定的,t=0,1,2….

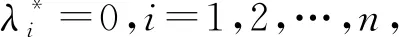
(4)

注意到严格下三角矩阵的性质:n个n×n的严格下三角矩阵相乘, 其乘积为零矩阵, 即：

(5)

反复套用式(4)，有：

然后证Lyapunov稳定性. 结合上述结论, 由(3)式有：

由此可得：

(6)

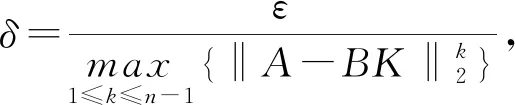
‖x(t)‖2<ε，t=1，2，3…n成立.

所以闭环系统式(3)是Lyapunov稳定的. 证毕.

注1 若假设1不成立, 只需存在状态反馈矩阵K, 能使得λi(A-BK)=0,i=1,2,… ,n, 定理1的结论同样成立.

3 仿真算例

表1 x(t)的模

表1相应的坐标图，如图1所示.

图1 x(t)的模

由图1可看出，系统的状态是有限时间收敛到零的.

4 结语

本文对离散时间系统提出了有限时间控制问题，并针对一类线性离散时间系统进行了有限时间控制设计，构建得到状态反馈控制律.利用矩阵运算，证明当反馈控制律作用于该系统时，闭环系统是有限时间稳定的.仿真算例也说明如此. 至于如何针对非线性离散时间系统进行相应的有限时间控制设计，则有待做进一步的探究.