基于MAA全温滞后模型的MEMS陀螺仪零偏补偿技术

吴 英，蒋 博，邸 克，邹新海，刘 宇

1. 重庆科技学院 智能技术与工程学院, 重庆 401331; 2. 重庆邮电大学 智能传感技术与微系统重庆市高校工程研究中心，重庆 400065)

0 引言

随着微机电系统(MEMS)技术的持续发展，MEMS陀螺仪技术逐渐成为人们的研究热点[1]。MEMS陀螺仪具有体积小、精度高、寿命长等优点，被广泛用于惯性导航与定位领域[2]；但也存在初始安装校准时间较长，器件材料对温度较敏感，角度积分误差随时间累积等缺点[3-4]。由于MEMS陀螺仪内部构造材料膨胀系数的差异会产生相应的热阻值和热应力[5-7]，环境温度的变化对陀螺零偏稳定性影响较大。

研究者从多方面对零偏补偿进行了研究，典型的补偿方法有：恒定参量激励法、滑动平均法及多元向量回归法等。文献[8]采用一种基于恒定参量激励的驱动控制方案，改善了小范围温度下降时陀螺仪温度敏感性，但缺少在宽温范围内的温度实验结果。文献[9]利用滑动平均法(MAA)对陀螺信号进行趋势项提取，减小了输出信号的时延问题。文献[10]使用一种基于支持向量回归的多元温度补偿方法，建立基于温度梯度的多元补偿模型，但在温度转折点处补偿效果较差。

以上研究仅对温度建立一个单一拟合曲线，对复杂温度变化下MEMS陀螺的零偏补偿效果较差。当环境温度升降循环变化时，陀螺的零偏误差并不是一条重合的曲线，而是多条有一定滞后偏移距离的曲线。

基于此，针对传统的MEMS陀螺仪的温度补偿模型难以解决由温度滞后变化引起零偏误差的问题，本文提出了一种基于MAA全温滞后模型的MEMS陀螺仪零偏补偿技术。

1 陀螺仪全温滞后模型

1.1 温度滞后原理

温度误差是 MEMS 惯性器件的主要误差之一。当环境温度变化时，材料热扩散速度有差异，引起陀螺结构尺寸、材料弹性模量和振动频率变化，从而引起零偏变化。温度的滞后性主要源于惯性器件的不同组成材料的热阻值和热应力各不相同，如缓冲胶的单位热阻值比陶瓷管的单位热阻值约高3个数量级。另外，由于温度传感器在固体上的空间位置不同而引起的测量误差，惯性装置中的金属和陶瓷外壳的温度滞后于传感器装置的输出温度，这也导致了温度滞后现象。

1.2 全温滞后模型

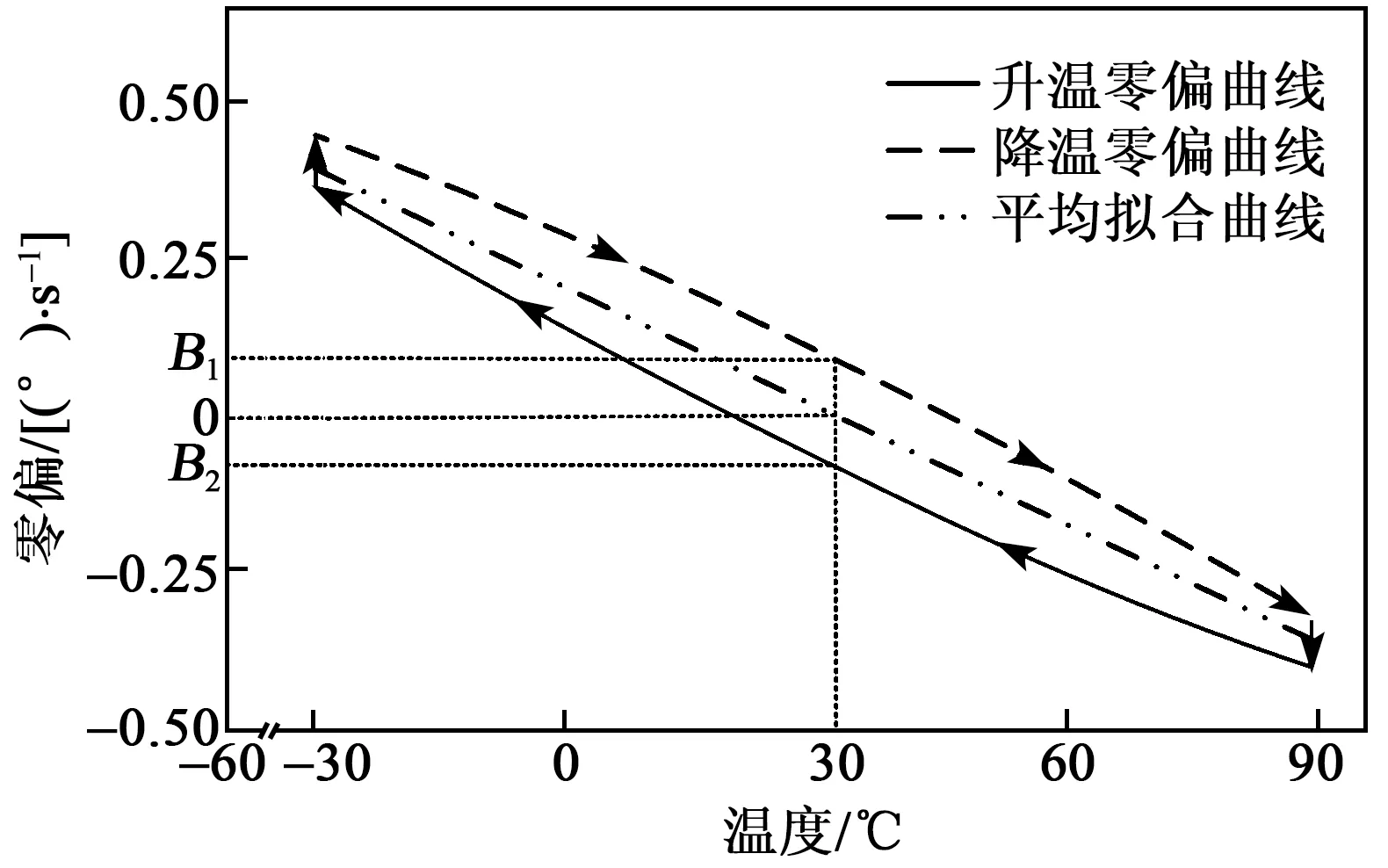
图1 全温滞后模型示意图

在安全额定温度范围内陀螺仪进行温度实验，温度滞后零偏的变化近似于梭型(或橄榄球型)。全温滞后模型示意图如图1所示。由图可见，其形状饱满、近似椭圆，反映出该结构的塑性变形能力和吸收震动能量的能力较强，具有良好的延展性。

首先设定30 ℃时的静态零位角度值作为温度误差基准值；然后温度循环实验测得的零偏值减去温度误差基准值，即为由温度变化引起的温度零偏值。在升降温度循环实验中，当温度回到30 ℃时，零偏B1、B2并未回到0 (°)/s，这种情况是由于温度的滞后性导致的现象，它将严重影响系统输出航向精度，因此需要对升温和降温分别建立补偿曲线，建立升降温度滞后零偏补偿模型，从而提高陀螺在环境温度循环变化下的零偏稳定性，减小温度滞后对陀螺仪精度的影响。

2 基于MAA全温滞后模型的零偏补偿技术

2.1 滑动平均算法

在离散动态实验数据中，利用区间离散点的函数值表示研究对象的真实变化规律。为了消除动态实验数据里的随机噪声波动，对于非平稳的陀螺仪数据，在一定长度的小区间上认为是稳定的。对其做局部求平均值的处理，过滤掉数据中的随机噪声，从而得到较平滑的数据曲线，即滑动平均算法。

在处理陀螺仪零偏数据过程中，对于一个长度为M的有序数据集合，按顺序滑动选取r个相邻数值，对每一个数值乘以一个比例权重系数，并相加求和，得到平滑的数据。

(k=p+1,p+2,…,M-q)

(1)

(k=s+1,s+2,…,M-s)

(2)

当p=0，q=r-1，θi=1/r，即左端点等权平滑法：

(3)

当p=-r+1，q=0，θi=1/r，即右端点等权平滑法：

(4)

本文对陀螺零偏数据采用右端点等权平滑法，如选取滑动步长r=9，通常用前9个零偏数据的均值来等效替换表示右端点，即第9个数据的测量结果：

g7+g8+g9)

(5)

对于滑动步长为r的右端点等权平滑法，它可以得到右端全部的值，但缺少左端头部的平滑滤波值，称为端部效应，即在区间[1,r-1]里的r-1个测量数据无法按公式(4)直接得到，需要额外补充录入。

2.2 全温滞后模型的零偏补偿技术

分析陀螺仪静态时温度零偏的滞后性，采用滑动平均算法对陀螺仪信号进行数据提取，提出一种升降温度滞后零偏补偿模型。对不同温度下的MEMS陀螺仪零偏进行标定，达到在全温变化范围内对陀螺仪零偏的精准补偿目标。MEMS陀螺仪的MAA温度滞后零偏补偿模型Hω(T)为

(6)

式中：f0，f1，f2，f3为拟合系数函数；T为MEMS陀螺仪温度；dT/dt为MEMS陀螺仪温度变化率。

实验中采样得到的数据都是离散化的，计算dT时，利用ΔT(现在时刻温度值减去前一时刻温度值)近似表示，即dT/dt=ΔT/Δt，其中设定采样频率为1 Hz，Δt为定值。因此，MAA温度滞后零偏补偿模型可近似简化为

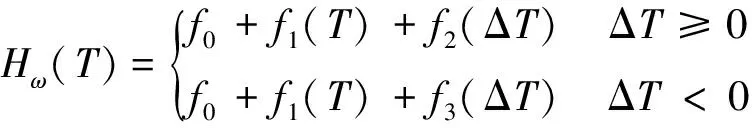
(7)

由于升温和降温时的零偏值有差异，若用传统单一曲线来拟合升降温度的零偏，得到的零偏误差较大。因此，不仅要采集此刻的温度值，还要考虑前一时刻的温度值，MAA升降温度补偿模型流程图如图2所示。本文以当前陀螺仪温度值T和温度变化率ΔT(此刻温度值减去前一时刻温度值)作为判断条件，分别通过传统补偿模型、升温模型(ΔT>0)和降温模型(ΔT<0)来补偿零偏误差。

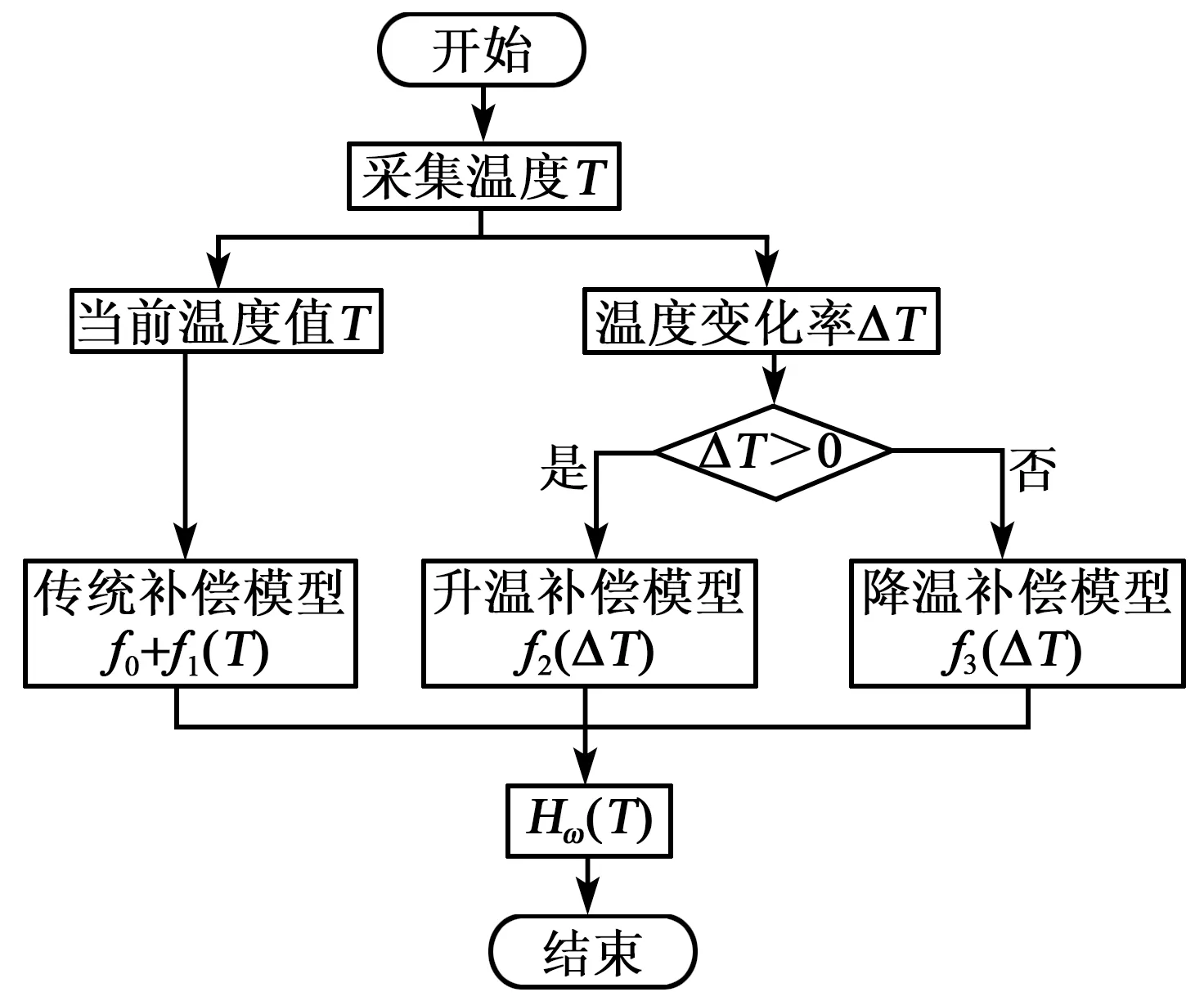
图2 MAA升降温度补偿模型流程图

3 实验与分析

3.1 实验过程

本实验选用SCR系列陀螺，ESPEC系列SET-A-04型号温箱，数据采集频率为1 Hz ，整体实验流程图如图3所示。

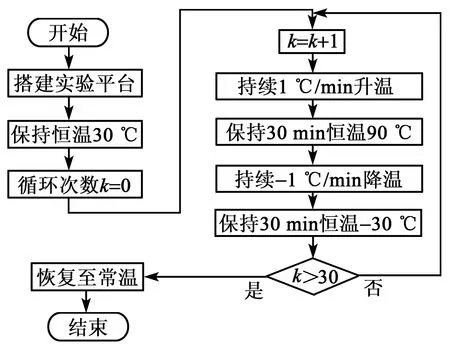
图3 整体实验流程图

实验步骤主要分为4步：

1) 温箱恒温30 ℃，对陀螺预热30 min。

2) 以1 ℃/min的速度持续升温，温度上升至90 ℃，保持恒温运行30 min。

3) 以-1 ℃/min的速度持续降温，温度降至-30 ℃，保持恒温运行30 min。

4) 重复2)、3)步实验30次。

在安全额定温度-30～+90 ℃进行实验，其中实验循环1次的时间-温度曲线图如图4所示。

图4 实验循环1次的时间-温度曲线

3.2 零偏补偿实验结果分析

首先选取局部温度变化区间-30～0 ℃和时间段 210～300 min的零偏变化数据进行分析，对应的局部时间、温度、零偏拟合曲线如图5所示。由图可见，温度从0降温至-30 ℃，保持-30 ℃恒温30 min，再升温至0。无滞后曲线的零偏随温度呈单一线性变化；有滞后曲线的零偏随温度呈现复杂曲线变化，在温度上升和下降趋势发生变化时，会暂时保持原有状态，从而出现温度滞后零偏的情况。滞后区间对应的时间持续约5 min，温度零偏相差约0.02 (°)/s。

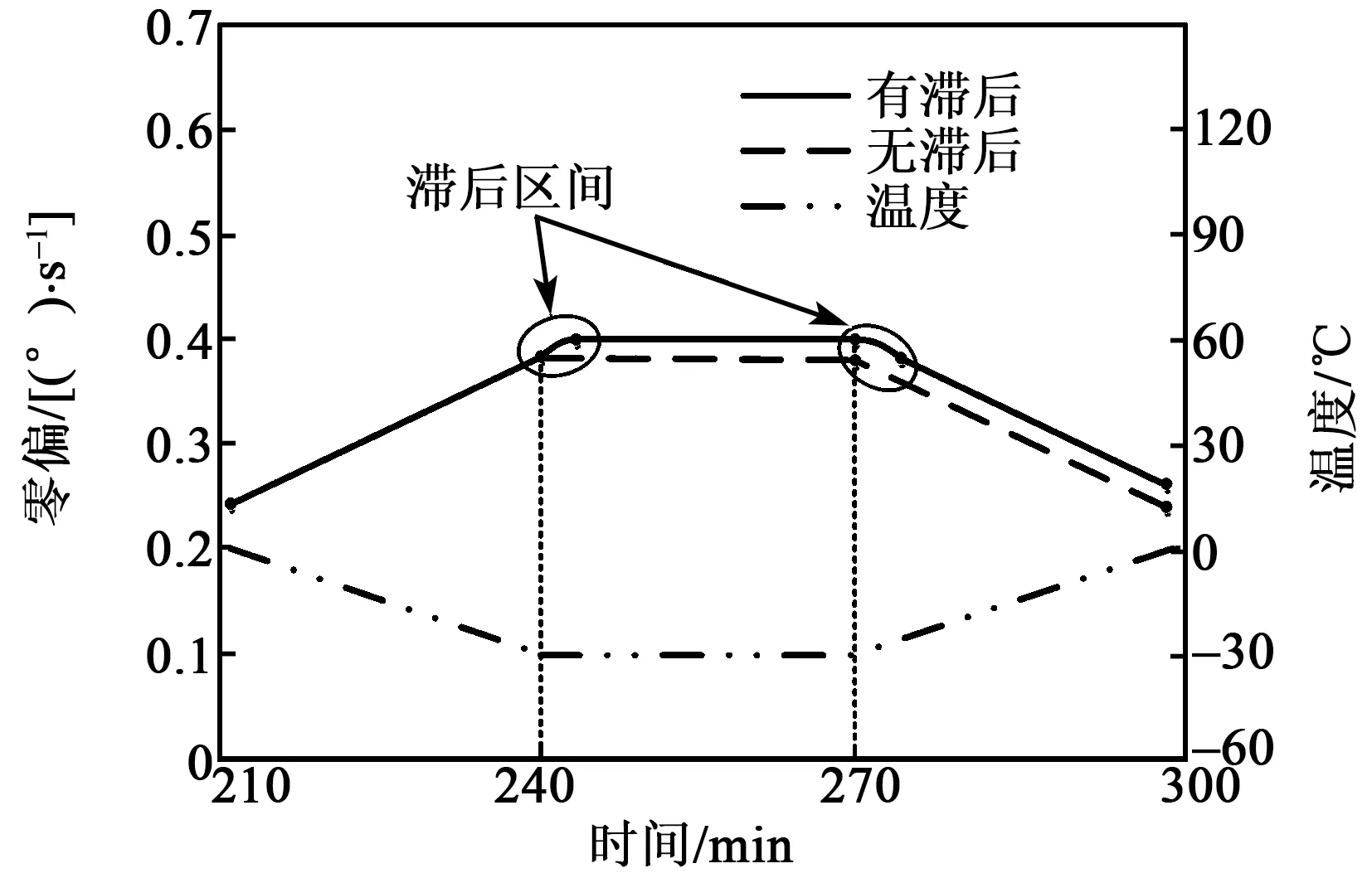
图5 局部时间、温度、零偏拟合曲线图

选取全温变化区间-30～+90 ℃的零偏数据进行整体分析，先对传统补偿模型进行试验，根据陀螺仪升温与降温时的初始零偏数据计算出平均拟合曲线，接着代入传统补偿模型得到补偿后的升降温度零偏输出值，对应的传统零偏补偿前、后对比图如图6所示。传统补偿前的初始升温、降温曲线是在-0.5～+0.5 (°)/s波动的倾斜曲线，而通过传统校准拟合曲线补偿后，变成在-0.1～+0.1 (°)/s波动的近似水平曲线。

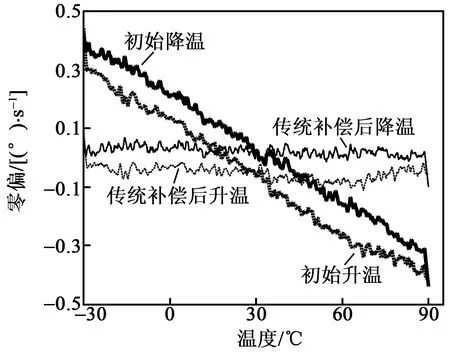
图6 传统零偏补偿前后对比图

对MAA补偿模型进行试验，根据陀螺初始零偏数据计算出校准拟合升、降温曲线，代入MAA升降温度滞后零偏补偿模型得到补偿后的零偏值，对应的MAA零偏补偿前、后的对比曲线如图7所示。通过MAA校准拟合曲线补偿后，变成在-0.04～+0.04 (°)/s波动的近似水平曲线。

图7 MAA零偏补偿前后对比图

分析对比MAA补偿法与传统补偿法的结果，对应的陀螺仪零偏补偿前、后参数变化情况如表1所示。零偏补偿前的零偏标准偏差为0.21 (°)/s。通过传统零偏补偿后的零偏标准偏差为0.06 (°)/s，其减小了近3倍；通过MAA零偏补偿后的零偏标准偏差为0.02 (°)/s，其减小了近10倍。由表可见，在减小温度滞后零偏误差方面，MAA补偿法优于传统补偿法，提高了近3倍。

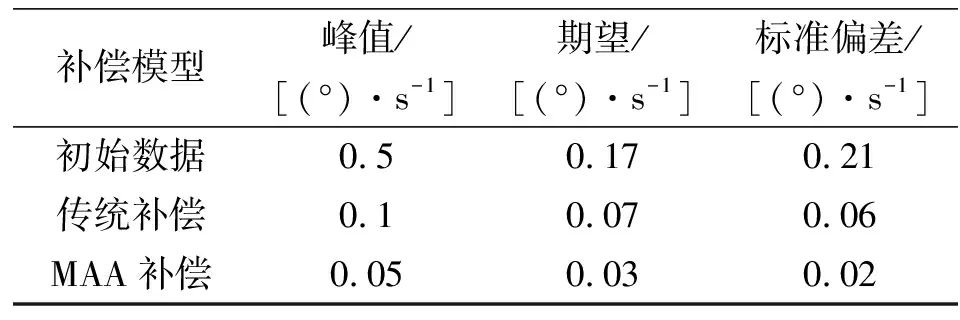
表1 零偏补偿前、后参数变化表

4 结束语

本文针对传统的MEMS陀螺仪的温度补偿模型难以适应温度滞后变化的问题，我们利用滑动平均算法建立温度滞后模型，采集升、降温情况下的零偏数据，并做出拟合曲线，对陀螺仪的零偏进行校准补偿。在-30～+90 ℃全温范围内的实验表明，通过MAA升、降温滞后零偏补偿模型，可将陀螺仪零偏标准偏差从0.21 (°)/s 降至0.02 (°)/s，零偏稳定性增加了近10倍。通过MAA全温滞后模型的零偏补偿技术，可以适应全温范围的温度变化，有效提高了MEMS陀螺仪的零偏稳定性和测量角度精度。