双模式压电粘滑驱动器设计与试验

段铁群，马颜龙，孟庆亮，田原实

1. 哈尔滨理工大学 机械动力工程学院，黑龙江 哈尔滨 150080;2. 北京空间机电研究所，北京 100094)

0 引言

压电驱动器具有分辨率高，尺寸小，无电磁干扰等优点，广泛应用于扫描显微镜、生物医药及光学制造等领域[1-4]。其中能实现大行程运动的驱动器称为步进式压电驱动器，根据其工作原理可分为超声驱动型、尺蠖驱动型及粘滑惯性驱动型等，各个类型压电驱动器均有各自的优缺点。超声驱动型是利用器件的谐振状态来驱动动子或转子运动，尤其擅长高速运动。如刘英想等[5]提出，采用一、二阶弯曲模态组合的方式设计的超声旋转马达最大空载转速可达158 r/min，但该类型驱动器分辨率低，磨损、发热严重。尺蠖型驱动器是以自然界中的尺蠖虫作为原型仿生研制的一种新型驱动器，通过驱动单元和钳位单元“驱动—钳位—驱动”交替动作的方式实现精密驱动，该类型驱动器具有较大的输出力，但结构和控制系统较复杂，运动速度较低。粘滑惯性型驱动器利用定子和动子间的动、静摩擦力差来实现驱动。周明星等[6]设计了一种利用双压电叠堆共同驱动的压电粘滑直线驱动器，嵌于桥式柔性铰链机构内的压电叠堆A用于调节摩擦力，嵌于平行四边形柔性铰链机构内的压电叠堆B用于驱动滑块运动，该驱动器可实现最大输出速度为3.27 mm/s的大行程直线运动，但该类型压电驱动器运动速度相对较低，无法实现快速定位。

针对现有各类型步进式压电驱动器无法兼顾速度和精度的问题，本文通过将谐振形式融入到粘滑型驱动器中的方式，设计了一种双模式压电粘滑驱动器，可实现高精度定位和快速响应的目的。

1 结构和工作原理

1.1 驱动器结构

图1为本文提出的双模式压电粘滑驱动器整体结构。固定基座和基板一体加工，固定基座用于固定安装，压电陶瓷片通过环氧树脂胶粘贴于基板中心，柔性放大机构的两端通过环氧树脂胶粘贴在基板两端，柔性放大机构和滑杆一体加工，滑块可在滑杆上自由滑动。固定基座、基板、柔性放大机构、滑杆及滑块均采用65Mn弹簧钢线切割加工而成。

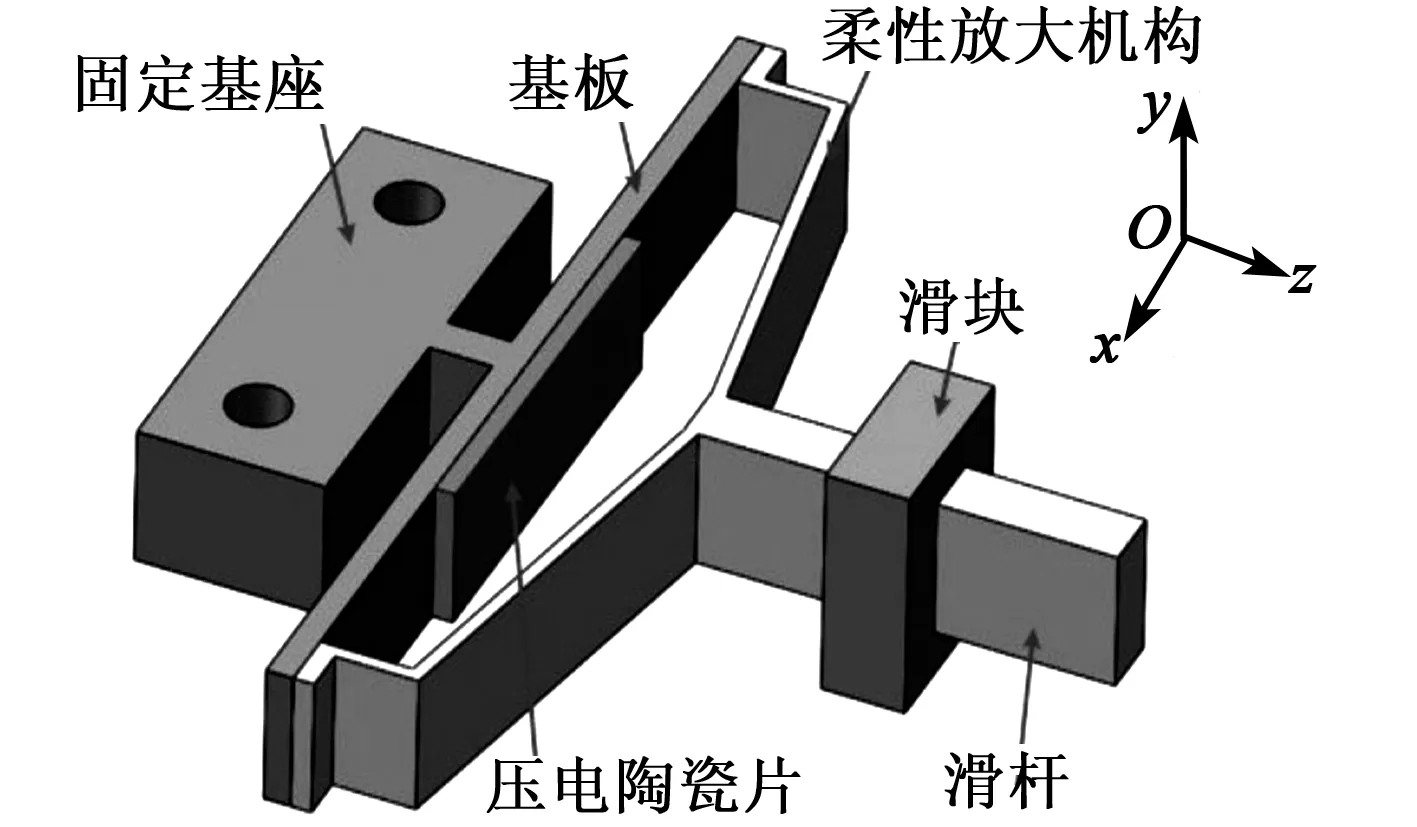
图1 双模式压电粘滑驱动器整体结构

1.2 工作原理

锯齿波型电信号被用来驱动双模式压电粘滑驱动器中的压电陶瓷片，其工作原理可分为非谐振模式和谐振模式。非谐振模式的工作原理如图2所示。

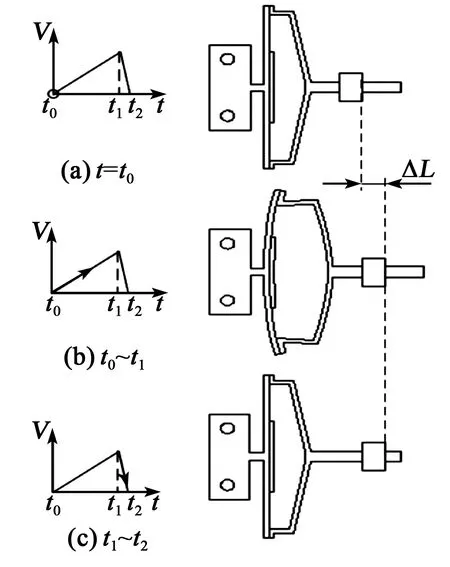
图2 本文所提出的压电驱动器非谐振模式工作原理

初始状态如图2(a)所示，每个运动周期分为两个步骤：

1) 从时刻t0～t1，压电陶瓷片缓慢弯曲，通过柔性放大机构的放大使滑杆向前伸长ΔL，在静摩擦力作用下推动滑块向前运动ΔL，如图2(b)所示。

2) 从t1～t2，压电陶瓷片快速恢复，因此，柔性放大机构和滑杆返回到其初始位置，由于惯性力的作用，滑块将保持位置如图2(c)所示。

通过重复步骤1)、2)，所设计的压电驱动器逐步实现大工作行程，该模式下工作分辨率较高。

谐振模式工作原理与非谐振式工作原理类似，但谐振模式工作频率在该驱动器的共振频率下完成，此时，滑杆向前伸长量ΔL1≫ΔL，因此，与非谐振模式相比，滑块的移动速度较快。

2 设计与分析

2.1 柔性放大机构参数设计

为了获得最优的驱动效果，应调整驱动器柔性放大机构的参数。本文提出的压电驱动器整体结构尺寸如图3所示，分别对柔性放大机构的参数角度β、长度比l3/l4及厚度d2进行有限元仿真设计。

图3 所提出的压电驱动器结构尺寸参数

驱动器除压电陶瓷片外所有材料均为65Mn钢，密度ρ=7 810 kg/m3，弹性模量E=1.96×1011N/ m2，泊松比μ=0.3。选择具有较高压电常数的陶瓷材料 PZT-4，矩形压电陶瓷片厚1 mm,其压电矩阵、刚度矩阵和介电矩阵分别为

1010(C/N)

(1)

(2)

(3)

在静力学分析过程中，2个安装孔上施加固定约束，给左、右弯曲压电陶瓷施加 100 V电压，网格划分如图4(a)所示，3种参数对变形的影响如图 4(b)～(d)所示。

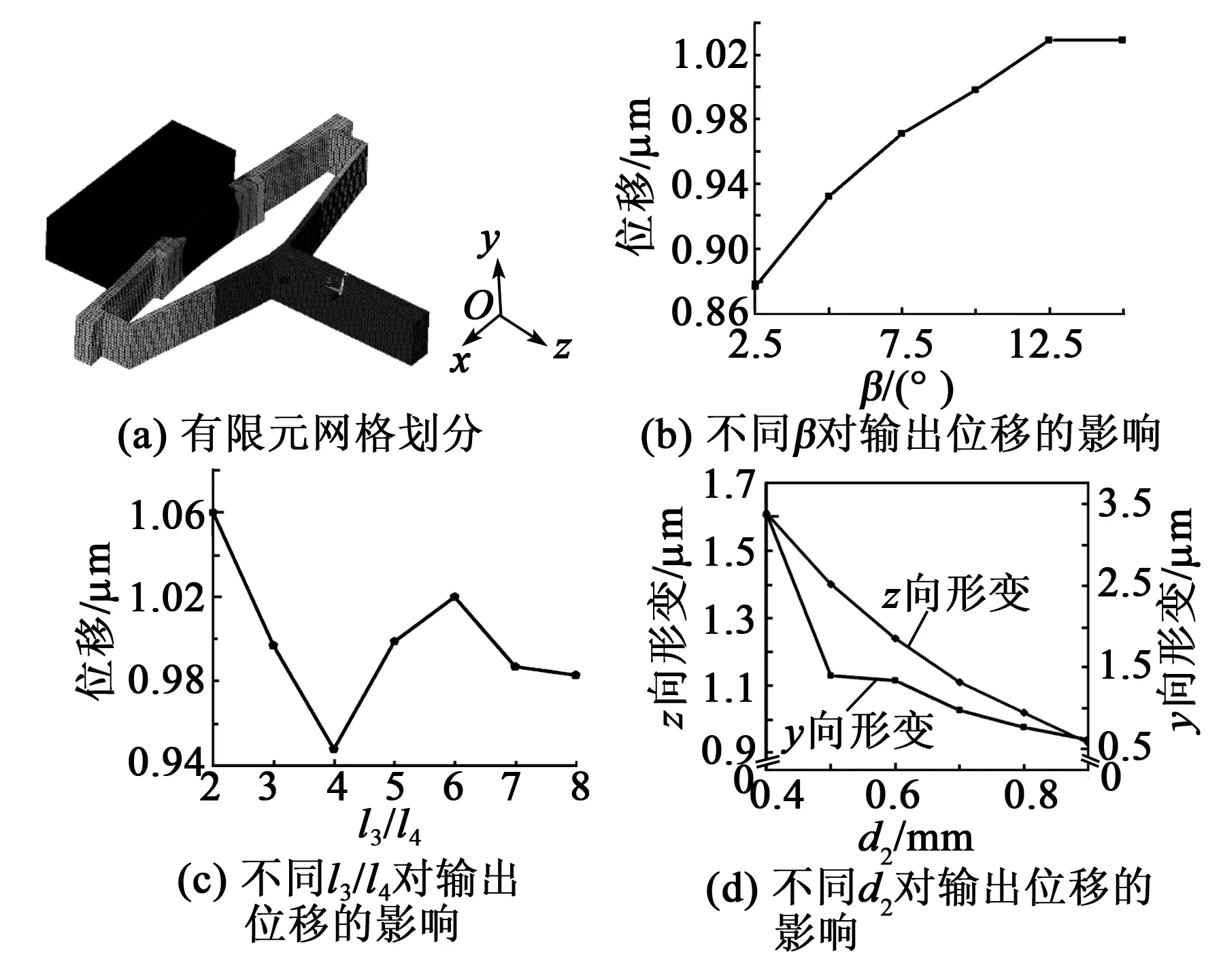
图4 有限元设计柔性放大机构参数

由图4可看出，随着β的增大，输出位移先增大后基本保持不变。l3/l4越小，说明驱动器在z向的尺寸越大，因此在选择l3/l4时，需综合考虑驱动器的z向位移输出和整体尺寸。柔性放大机构的d2对驱动器整体刚度影响较大，因此，为了选择较优参数，仿真时当给驱动器滑杆的末端沿-y向施加一个0.01 N的力，驱动器滑杆末端的输出位移如图4(d)所示。由图可看出，随着d2的增大，z向输出位移逐渐降低；沿-y向施加一个0.01 N的力，当d2>0.7 mm时，y向输出位移小于z向输出位移。

综合考虑尺寸小型化，输出稳定性等因素，选择β=10°，l3/l4=6，d2=0.7 mm的3种参数加工柔性放大机构。

2.2 驱动器模态分析

为了使驱动器能实现非谐振与谐振双模式的工作形式，需对其谐振状态进行模态仿真，确定哪一阶振型适合作为驱动器的工作振型，同样，在有限元模态仿真过程中，给固定基座上的两孔施加位移全约束，驱动器前4阶模态如图5所示。其前4阶共振频率分别为466.25 Hz，739.96 Hz，828.57 Hz，1 697.1 Hz。由图可看出，只有三阶模态振型的滑杆是沿z向伸缩变形，因此，证明了该驱动器可实现双模式的驱动。

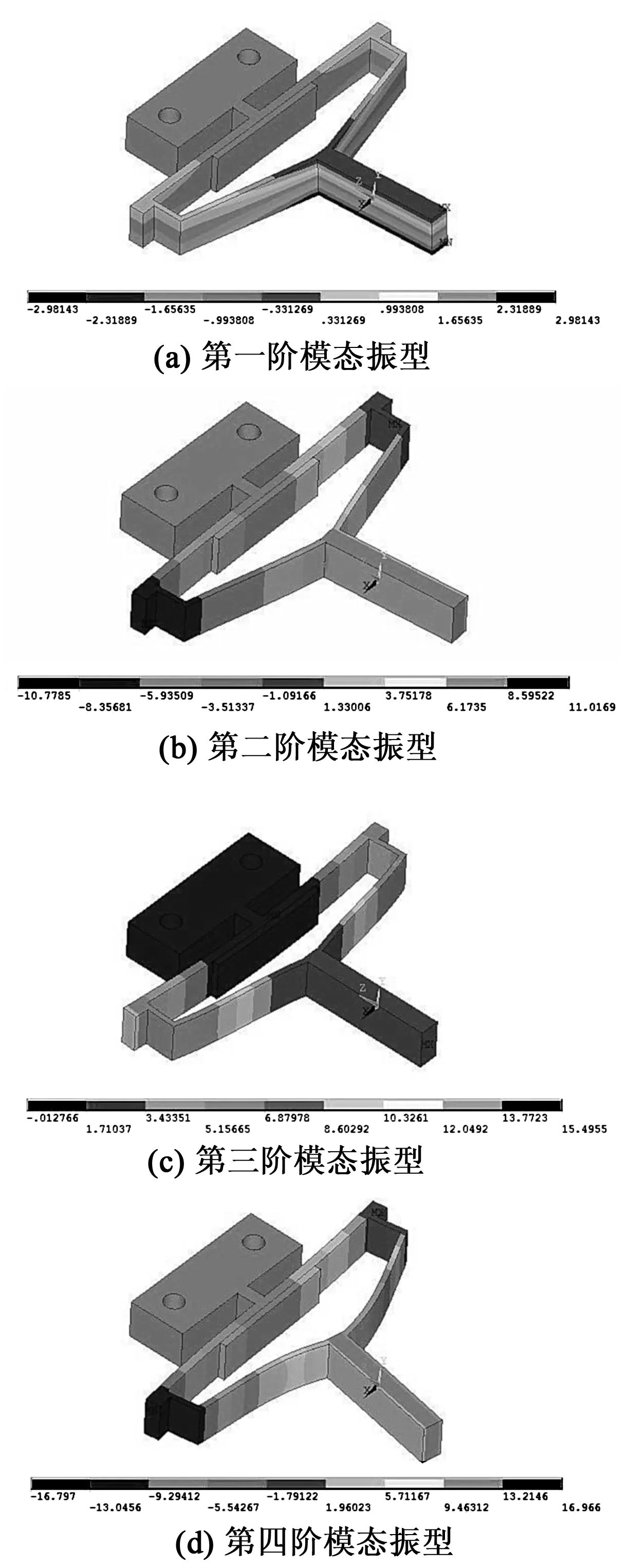
图5 前4阶模态振型

2.3 驱动器动力学分析

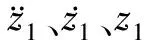
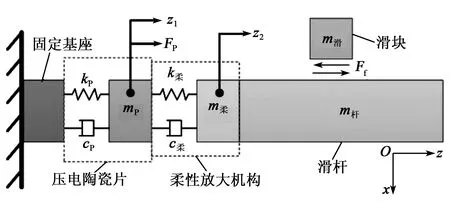
图6 整机动力学模型

对压电单晶片、柔性放大机构和滑块分别进行受力分析，如图7所示。

图7 压电单晶片、柔性放大机构和滑块受力情况

压电单晶片、柔性放大机构和滑块的动力学方程分别为

(4)

(5)

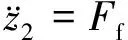
(6)

联立式(4)～(6)可得整机动力学方程：

kPz1+k柔z2=FP-Ff

(7)

3 驱动器性能测试

3.1 搭建实验平台

图8为搭建的试验测试系统。在该实验系统工作的情况下，信号发生器产生锯齿波电压信号，通过功率放大器(RH41-D)放大该电压信号。激光传感器(LK-H020)测量滑块的运动。激光传感器测得的所有数据都由计算机进行处理和保存。

图8 双模式压电粘滑驱动器试验测试系统

3.2 性能测试

本文所有实验均在占空比100%的锯齿波电信号下进行。驱动电压与步距的关系如图9所示，设置驱动频率f=1 Hz。

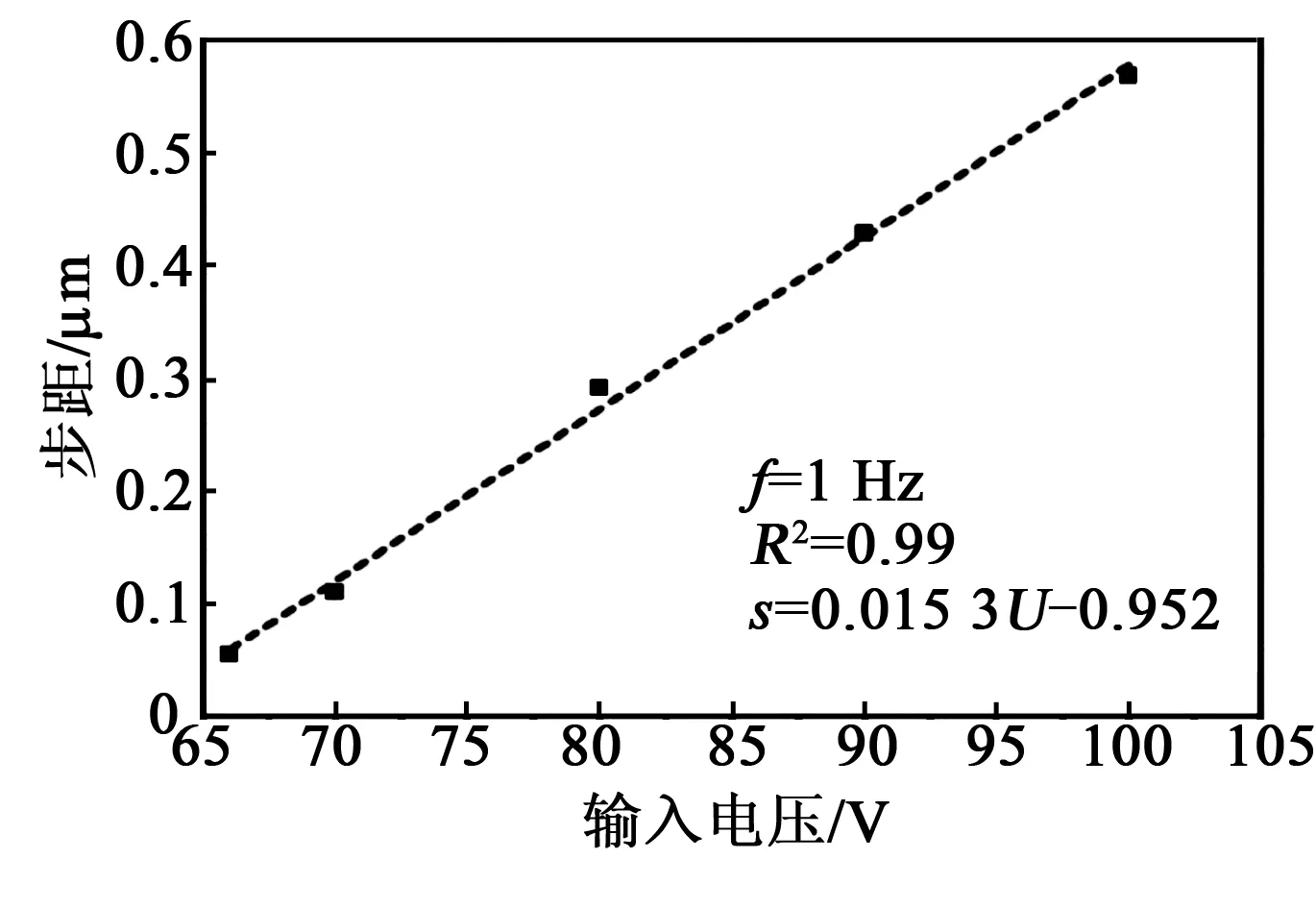
图9 1 Hz驱动频率下驱动器步距-电压关系曲线

由图9可看出，随着驱动器驱动电压升高，步距增加；当驱动电压为100 V时，最大步距约为0.569 μm；当驱动电压低于66 V 时，驱动器不能稳定工作，最小步距为0.054 μm。最小步距即为本文提出的压电驱动器的分辨率。驱动器的步距与驱动电压的线性关系为

s= 0.015 3U-0.952

(8)

式中：s为驱动器步距；U为驱动器的输入电压。线性拟合度R2= 0.99。

驱动频率是影响驱动器性能的一个重要因素，本文提出的双模式压电粘滑驱动器的两种工作模式主要通过频率来区分。非谐振模式下的速度、步距与频率关系如图10(a)所示。在非谐振模式下(主要是f< 400 Hz情况下)，驱动器的步距保持在ΔL=0.56 μm附近，此时，f是使滑块运动速度升高的主要原因，滑块移动速度随着f的增加而增加。驱动器的输出速度v与f的线性关系为

v= 0.55f-0.15

(9)

此时R2=0.99，这证实了所提出的双模式压电粘滑驱动器在非谐振模式下,其输出性能的稳定性。

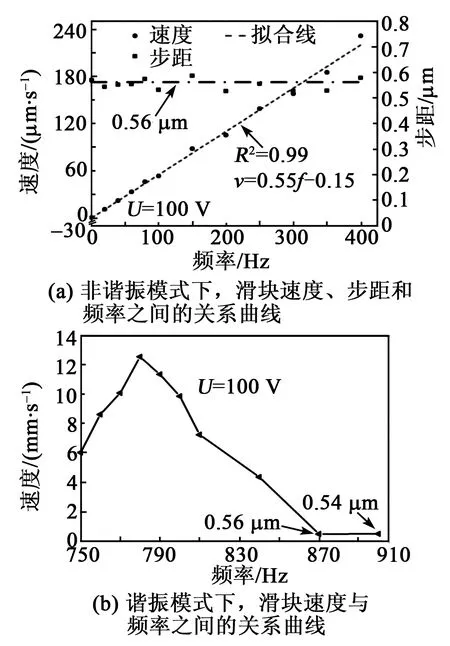
图10 两种模式下，驱动频率对输出性能的影响

谐振模式下,v与f的关系如图10(b)所示。在频率780 Hz左右时，驱动速度较大，最大可达12.56 mm/s。当频率超过870 Hz时，驱动器步距降到和非谐振模式相同的0.56 μm左右。在模态仿真分析时得到的三阶谐振频率为828.57 Hz，而实验结果的最大速度出现在780 Hz附近，与仿真结果出现偏差，分析主要原因为压电陶瓷片的粘贴存在偏差。

图11为双模式压电粘滑驱动器的输出速度-负载关系曲线图。非谐振模式下输出速度-负载关系曲线如图11(a)所示。当f=1 Hz时，最大负载约为1.2 N，驱动器的速度与负载F的线性关系为

v= -0.426F+ 0.48

(10)

此时R2=0.9。

图11 双模式压电粘滑驱动器输出速度-负载关系曲线

当f=780 Hz时，最大负载约为1.4 N，稍大于非谐振模式下的最大负载，驱动器的速度与负载的线性关系为

v=-9 108.26F+10 736.97

(11)

此时R2= 0.87。

4 结束语

本文提出了一种双模式压电粘滑驱动器，通过压电单晶片和柔性放大机构相结合实现高精度非谐振工作模式和高速度的谐振工作模式。通过有限元法获得了合适的柔性放大机构参数，并分析验证了驱动器双模式工作的可行性。实验结果表明，在非谐振模式下，样机可实现最小步距为0.056 μm，最大输出负载为1.2 N；谐振模式下，样机的最大输出速度为12.56 mm/s ，最大输出负载为1.4 N。