三段式扑翼飞行器气动特性的仿真研究
2020-07-07赵卫凯李文彬
赵卫凯,李文彬,黄 灿,吴 杰
(南京理工大学智能弹药技术国家重点实验室, 南京 210094)
扑翼飞行器在低雷诺数下的气动特性是其研究过程中的一大难点,早在1909年Knoller和Betz[1]发现二维翼型在扑动过程中可同时产生升力和推力;1975年Weis-Fogh解释了昆虫升力产生的拍合机制[2];1997 年,Van Den Berg 等在对飞蛾飞行的研究中发现了“延时失速” 机制[3],并在后来被Dickinso等在果蝇模拟实验中得以证实;曾理江等研究蜜蜂飞行时翅膀的气动特性[4];孙茂等用Navier-Stokes(N-S)方程计算了柔性翼的气动特性[5];黄鸣阳、昂海松等设计出了一款多段柔性仿鸟折叠翼模型[6-8]。
目前,对扑翼飞行器的气动研究主要依靠数值模拟和风洞实验,且研究对象多为仿昆虫的单段式扑翼,建立的扑翼模型为“拍动+扭转”的两自由度模型。近年来,通过分析鸟类翅膀的拍动过程,在扑翼模型中引入折叠这一运动,建立了“拍动+折叠+扭转”的三自由度模型[9-10]。
以往的单段翼模型[11]是以小翼展、高频率拍动的昆虫为仿生对象,主要描述的是扑翼沿翼展拍动运动和沿翼弦的扭转运动,并不适用于鸟类这样的大型飞行生物,因为该模型也未考虑过鸟类翅膀拍动过程中的弯曲折叠问题。近年来建立的两段翼模型[12]具有3种运动:翼展方向的拍动,翼弦方向的扭转和内外翼之间的弯曲折叠,并采用分段建模的方式来达到近似柔性的效果。
本文以鸽子为研究对象,建立“拍动+内折叠+外折叠+扭转”的三段式扑翼模型,用XFlow仿真软件进行气动仿真,主要研究低雷诺数下,三段式扑翼的各参数对飞行器气动力的影响,为三段式扑翼的设计奠定基础。
1 三段式扑翼模型的建立
1.1 鸽子飞行的高速摄影的分析
对鸽子的飞行过程进行高速摄影,观察各个飞行周期内鸽子翅膀的拍动图片。分析发现以往的两段式扑翼模型只解决了鸟类翅膀拍动过程中的内外翼的主动折叠问题(内折叠角,图1中的A处),但并未考虑到鸟类在实际飞行中,在气流的作用下,翅膀周围的羽毛会因自身的柔性而发生被动折叠(外折叠角,图1中的B处),本文主要研究的是翼尖羽毛的被动展向折叠现象,分析内外折叠角共同作用下扑翼的气动特性。
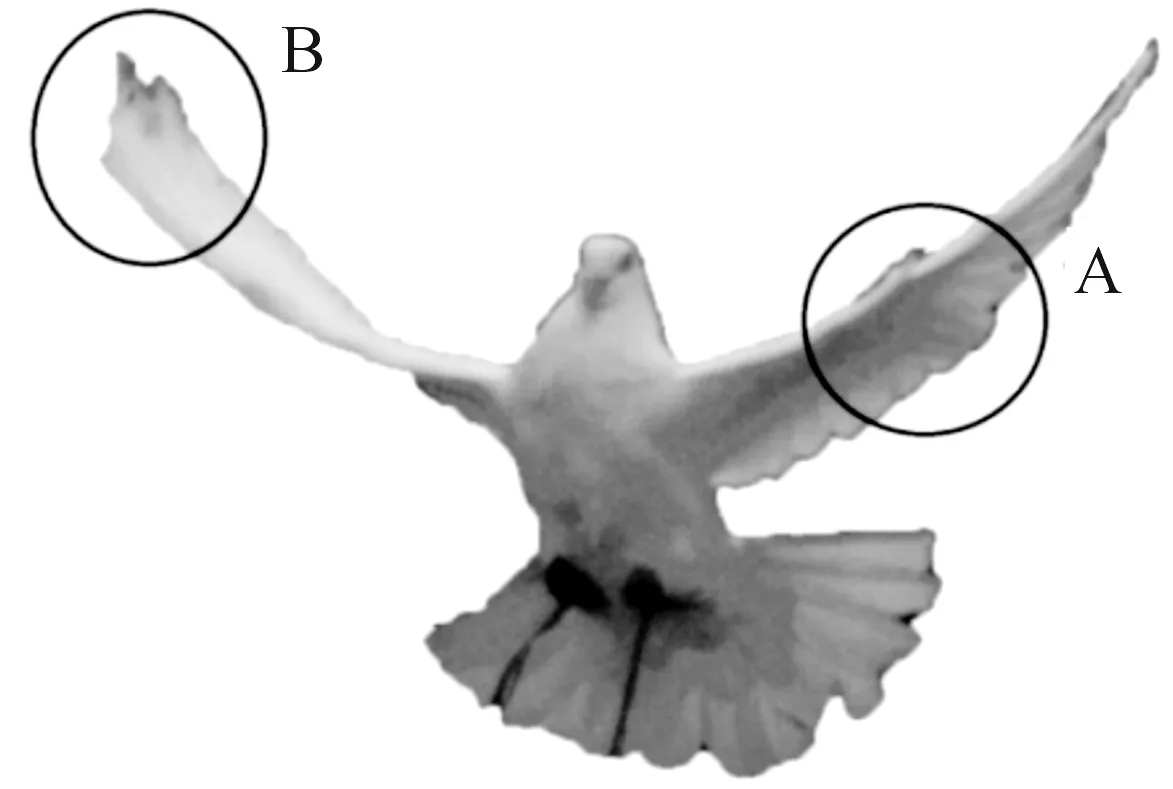
图1 鸽子高速摄影图片
因此,本文建立一个简化的三段式扑翼模型,来描述翅膀扑动过程中的这内外折叠现象。
1.2 三维建模
针对上述分析的主要现象,进行适当的简化,建立的三维模型主要包括机身和左右两翼,扑翼由翼根到翼尖依次分为A、B、C三段,其中内翼为A段,翼展为100 mm,外翼由B、C两段组成,合翼展为200 mm,翼根处翼弦为100 mm,A、B两段连接处翼弦为200 mm,且A翼面为梯形,B、C两段共同组成四分之一椭圆,如图2所示。
根据对鸽子飞行过程高速摄影得到的图像进行分析,可将扑翼飞行的复杂运动简化为:翅膀上下拍动和扭转、内外翼的折叠、翼尖折叠,三维模型如图3所示。

图2 右翼面二维平面图

图3 扑翼飞行器的三维模型示意图
图3中β是内翼的拍动角,δin和,δex分别为扑翼的内外折叠角,还有扑翼的扭转角设为α。其中扭转角为翅膀绕翼展方向转动时,内翼面与机身水平面的夹角。
扑翼截面应选用带弧形弯曲的翼型[13],此处采用上表面弧形、下表面内凹的S1223翼型,文献[14]对6种翼型进行仿真对比,发现S1223具有最大的升力系数,适中的推力系数。飞行器的三维模型如图3所示,其中机身长300 mm,翼展660 mm,内翼展为100 mm,外翼展为200 mm。
另外鸟类翅膀扑动会发生柔性变形,建立刚柔性混合扑翼模型,其中A段翼定义为刚性翼,B、C两段按适当宽度分段建模,模拟扑翼的柔性部分。
2 扑翼运动模型的定义
2.1 拍动函数
本文以分段建模为基础,A、B、C三段分别代表扑翼的内翼、外翼、翼尖,并分别列出各自的运动方程。其中A段翼只描述翅膀的拍动,B段翼描述拍动角和内折叠角,C段翼描述拍动角和内外折叠角。此外,扑翼飞行还需要考虑急回特性,即下扑阶段所占时间为整个扑动周期的60%~80%,此处选为75%,对扑动过程的语言描述如下:
1) 下扑阶段:翅膀由最高处开始下扑,在最高处,各段翼保持平直,随后,在下扑过程中,内外折叠角逐渐展开,达到最大值后,保持内外折叠角度最大值继续向下扑动,快到最低处时,折叠角缓慢收敛,在最低处,折叠角归0,各段翼又保持平直。在下扑的同时,翅膀做扭转运动,从而产生向前的推力。
2) 上扑阶段:翅膀到达最低处后,扑翼向内折叠,快速上扑,内外折叠角也是缓慢打开,保持最大,然后收敛的过程,但因为急回特性的存在,这一过程相对于下扑阶段的要快。同样,在上扑的同时,翅膀也在做扭转运动,产生推力。
综上,结合急回特性和分段近似柔性的思想后,各翼段的扑动函数如下所示:
1)A段翼,参考文献[11],以单段翼扑动函数为模型:
(1)
2)B段翼,与A段翼之间会有一个内折叠角:
(2)
(3)
(4)
其中,内折叠角为:
δin=δ1
(5)
βBx(t)表示B段翼中第x小段机翼扑动角函数,xB为B段翼的第x小段,nB表示B段翼共分为nB段,βB(t)表示B段翼末端处的扑动角函数。
该段翼参考了分段近似柔性思想,并从鸽子飞行的高速摄影图像分析,发现无论在上拍,还是下拍阶段,内折叠角都有一个完整的展开、保持最大、收缩的过程,因此,内折叠角作为一个独立的函数存在,有自己的折叠幅值,且折叠频率应大于内翼拍动频率,不再用内翼扑动函数的相位差形式[12]来描述;
3)C段翼,与B段翼之间会有一个外折叠角:
(6)
(7)
(8)
其中,外折叠角为:
δex=δ2-δ1
(9)
βCx(t)表示C段翼中的x小段机翼扑动角函数,xC为C段翼的第x小段,nC表示C段翼共分为nC段,βC(t)表示C段翼末端处的扑动角函数。
2.2 扭转函数
扑翼在上下拍动折叠的同时,也在进行扭转运动,且大鸟实际拍动时,外部扭转大,内部扭转小。
(10)
(11)
f表示扑翼扑动频率,φ表示扭转滞后角,αx(t)表示第x小段扑翼的扭转角,α(t)表示翼尖的扭转角,n表示扑翼共分为n段。
考虑进急回特性后,上式中各翼段在各个时刻的扑动频率分别为:

(12)
运动参数设置如表1所示。

表1 扑动参数设置
在XFLOW中按公式编写程序,得一个周期内扑翼的拍动过程,如图4所示。
3 数值仿真
3.1 仿真环境设置
本文选用XFlow软件进行仿真,XFlow是基于玻尔兹曼方法的流体仿真软件。XFlow采用无网格技术,由系统在后台自动绘制网格,与Fluent[15]相比节省了大量绘制网格的时间。
将流场域设置为4 m×2 m×2 m的模拟风洞,y轴正方向指向扑翼飞行器正上方,流体速度指向x轴正方向,z轴正方向指向左翼翼展方向。计算域流体为空气,且软件仿真中无风动壁面和支撑系统对来流进行干扰。计算模型选用单相外部流绝热模型,其他仿真参数设置如表2。

图4 一周期内扑翼运动过程示意图

表2 仿真参数设置
在计算域的设置中,还需要考虑风洞的阻塞比问题,即当风洞的阻塞比大于2%时,需要修正阻塞干扰产生的误差。阻塞比设为δ:
δ=Sn/S
(13)
Sn为扑翼飞行器沿x轴正方向的投影面积,S为风洞气流入口的面积,由XFlow导出模型参数可知,前者值为0.031 7 m2,后者值为4 m2,计算得阻塞比为0.79%,因此不需要进行对阻塞干扰的修正。
3.2 参数选择
影响扑翼飞行器气动特性的参数有很多,比如扑动频率、机身迎角、内外翼折叠角等。本文主要研究扑翼飞行器的内外折叠角对飞行器气动特性的影响,拟要研究的参数有折叠角个数、内外折叠角幅值、外折叠角的折叠位置(用C段翼的长度来表示)等。
其中,当没有折叠角存在时(0折叠),表示单段翼;当只有内折叠角存在,即为1个折叠角飞行(1折叠),表示两段翼;内外折叠角都存在,则为2个折叠角飞行(2折叠),表示三段翼。本文采用控制变量法,设定多个研究参数,将其中一个参数设为变量进行对比分析,变量范围设置如表3。

表3 变量范围
4 仿真结果分析
在数值仿真中,内翼拍动幅值为60°,扑动频率4 Hz,仿真时长1.5 s,按鸽子飞行速度,设置来流速度为10 m/s,计算时间步长为0.001 ms,帧频率为100 Hz,并采用无量纲数平均升力系数Cl和推力系数Ct来衡量升力和推力。
对XFlow仿真出的数据进行处理,得到无折叠角的情况下,扑翼飞行器的平均升力系数为0.347,平均推力系数为0.902。
4.1 内外折叠角幅值对气动特性的影响
从XFLOW中导出不同内外折叠角下升力系数与阻力系数的数据计算平均值,得图5、图6。

图5 内外折叠角幅值对平均升力系数的影响曲线
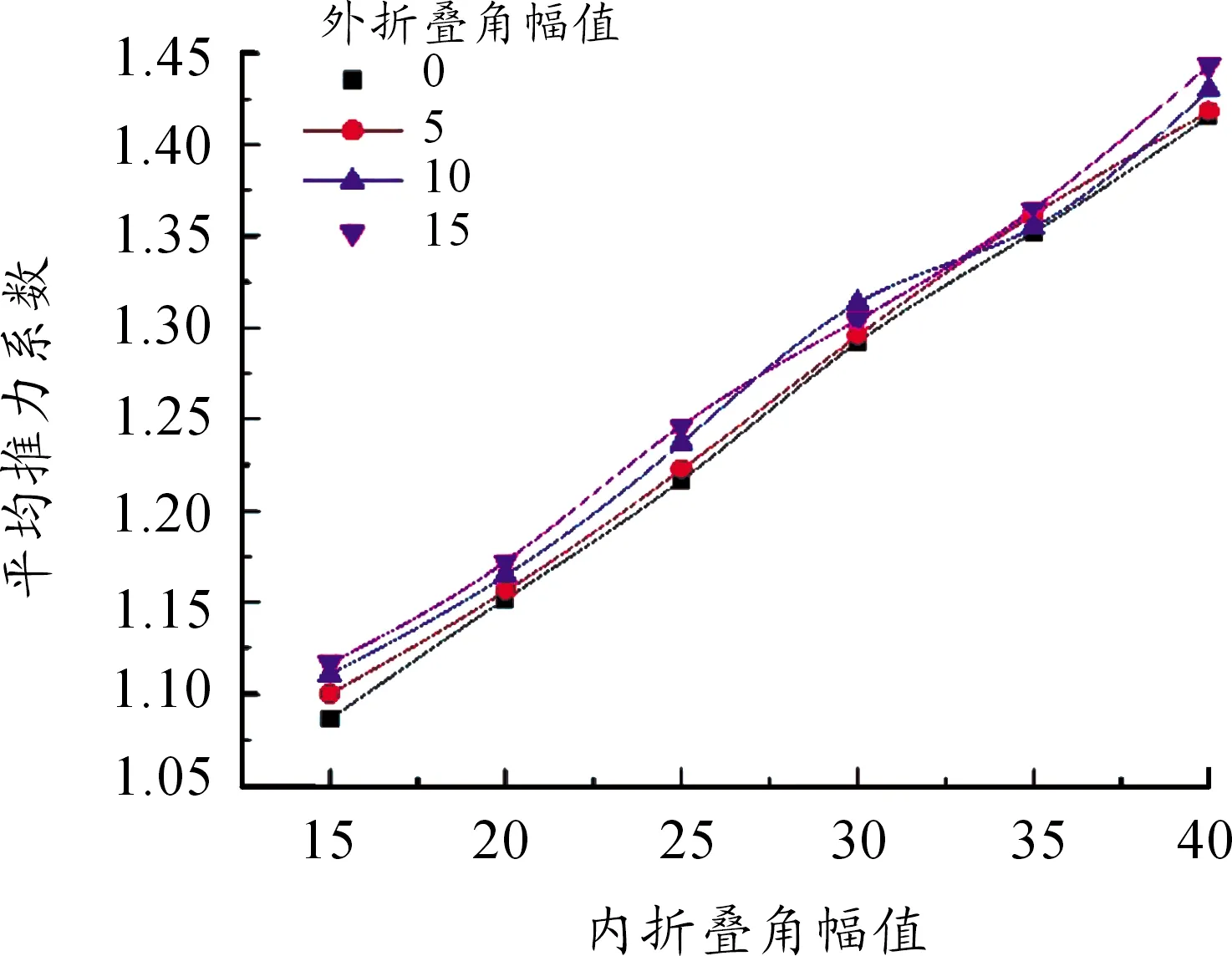
图6 内外折叠角幅值对平均推力系数的影响曲线
首先是平均升力系数,当外折叠角幅值不变时,平均升力系数随着内折叠角幅值的增加而增加,当内折叠角幅值不变时,平均升力系数也随着外折叠角幅值的增加而增加。但当两者联合作用时,呈现出复杂的非线性增长关系,这种非线性会随着外折叠角幅值的增加而更加明显。
其次在平均推力系数方面,当外折叠角幅值不变时,平均推力系数随内折叠角幅值的增加而增加,但当内折叠角幅值不变时,平均推力系数基本不会受到外折叠角幅值的影响。
因此推测:内折叠角是影响扑翼升力和推力的主要因素,而外折叠角进对推理几乎无影响,对升力的影响远小于内折叠角。
原因是:外折叠角幅值远小于内折叠角,折叠过程对迎风面积的改变极小,故飞行器推力几乎不变;但又因折叠作用,气流加速绕过翼尖,产生压力差,从而对升力有小幅增加。
4.2 与无折叠、单折叠飞行器的对比分析
从XFlow中导出0折叠、1折叠、2折叠的仿真数据,运用Origin绘制曲线,得图7与图8。

图7 不同折叠角个数下的升力系数曲线
图7中,下拍阶段的正升力峰远小于上拍阶段的负升力峰,且下拍时,带折叠角的升力峰大于无折叠角的升力峰,这是因为急回特性的作用,上拍阶段所用时间仅占拍动周期的25%,上拍至最高处需要更高的拍动频率,拍动频率越高,产生的气动力越大,因此负升力峰才会出现急剧的增加。

图8 不同折叠角个数下的推力系数曲线
同理,在图8中,下拍时的推力峰值,会因为折叠角的出现而又明显的增益,但与 由翅膀的扭转运动产生的,其方向指向飞行方向。而升力是由翅膀上下拍动产生,一个周期内升力有正有负,但总升力仍为正值。
观察两图发现,带折叠角的气动特性远优于无折叠角的扑翼模型,且在图7、图8中折叠角个数的影响几乎分辨不出。结合1.1节对高速摄影的分析和4.1节中的推论,再次说明折叠角会增加扑翼飞行器的升力和推力,但不同折叠角下气动力变化曲线接近一致,而均值不同,可见内折叠角在气动力增益中起主要作用,而外折叠只能小幅增加飞行器的气动力。
对推力几乎无影响的原因是:翅膀在拍动过程中,外侧羽毛会出现展向和弦向两个方向的被动折叠,而本文所建的简化模型主要研究展向折叠现象,未考虑外侧羽毛的弦向扭转(图9展示羽毛的弦向扭转过程)。按照翅膀上下拍动时,气流产生升力,前后扭转时,气流产生推力的飞行机理,故此推测羽毛的展向折叠影响升力,弦向扭转影响推力。但该推测是否成立,需要进一步的研究论证。

图9 外侧羽毛的弦向扭转
4.3 各翼段所受气动力矩
从XFlow中导出右翼A、B、C三段翼各自的升力力矩Ml和推力力矩Mt数据,得图10与图11。其中力矩的叶素法计算公式如下:
(14)
(15)
图10和图11中,各翼段的升力力矩和推力力矩也呈周期性变化,且因急回特性,负力矩峰值大于正力矩峰。另B段翼的升力力矩和阻力力矩都是最大的,这是因为B段翼拍动时的受力面积最大,经叶素法的积分值最大。

图10 各翼段升力力矩变化曲线

图11 各翼段推力力矩变化曲线
结合式(13)和式(14)可知,翅膀拍动产生气动力有着周期性的变化规律,其中B段翼,也就是外翼,是产生气动力矩的主要部位。
5 结论
1) 内折叠角可明显增加扑翼飞行器的升力和推力,但外折叠角却只能小幅增加飞行器升力,对推力几乎无影响。
2) 升力和推力都呈现出周期性变化,且因为急回特性的存在,上拍阶段的升力峰和推力峰都会大于下拍阶段的峰值,这也说明气动力的大小与拍动频率呈正比。带折叠角扑翼的升力和推力会明显高于无折叠角扑翼,不同折叠角数目下的曲线却十分接近,再次说明内折叠角是改变气动力的主要因素。
3) 观察各翼段的升力矩和推力矩发现:气动力矩呈周期性变化,且负力矩峰大于正力矩峰,外翼是扑翼产生气动力和气动力矩的主要部位。
