变化电流产生感生电场之电磁感应规律

摘 要：通过电磁感应实验，本文总结了一个电磁感应规律，同时指出了麦克斯韦方程的一个不足。

关键词：变化电流;感生电场;感应电流;电磁感应规律

1 电磁感应规律

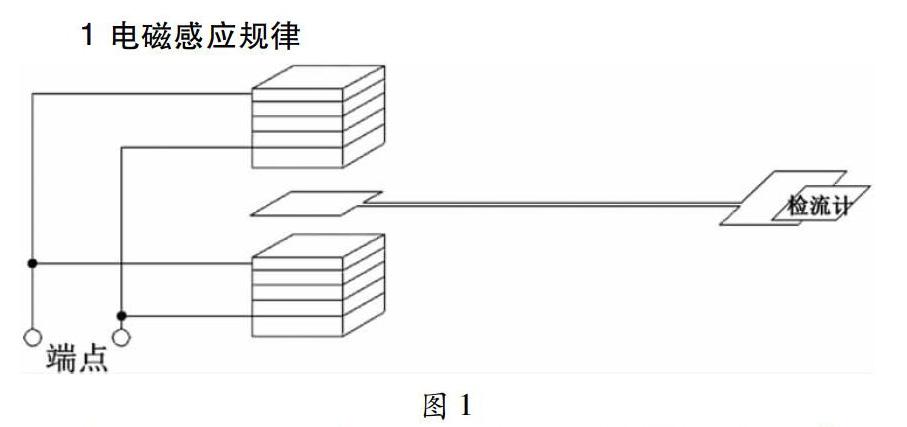
如图1所示，将绝缘导线密绕在两个边长约31厘米的正方体木块上（为了画图方便，导线画稀疏了），导线直径约1毫米，在两个正方体上密绕的导线匝数相同，加上密绕导线后上下平行摆放的两个木块之正方形面边长约为31.2厘米，将密绕两个木块的导线如图相互连接形成两个导线端点用来连接电源。将被感应导线在两个木块中间围成边长约31.2厘米的正方形后导线两端紧挨着射线状平行延伸远离木块连接检流计形成闭合回路，此正方形和两个木块对齐且和两个木块之邻近的两个面平行。用1节1号干电池连接两个导线端点，接通或者断开电源的瞬间，检流计指针最大摆幅约到8.1。

使用相同的被感应导线（用同一根导线是为了电阻一致），将其围绕形状由正方形改为圆形，圆形和正方形的周长相等，而后导线两端紧挨着射线状平行延伸远离木块连接检流计形成闭合回路，此圆形和前面所围的正方形为同一中心，此圆形也和两个木块之邻近的两个面平行，用1节1号干电池连接两个导线端点，接通或者断开电源的瞬间，检流计指针的最大摆幅约为6.3，改变圆的直径，无论改成任何尺寸，实验都显示检流计指针最大摆幅小于6.8，6.8小于8.1。

此实验之所以受感应导线中产生感应电流，其根源在于受感应导线中的自由电子受到了感生电场的作用，受感应导线所围成的图形沿着感生电场时产生的感应电流才最大。以上实验显示，被感应导线围成正方形比围成圆形时产生的感应电流大;实验还显示，围成其它边长的正方形产生最大感应电流时电流计指针的最大摆幅接近7.8，7.8也小于8.1。

以上实验说明感生电场是顺着变化电流的，说明变化电流在某处产生的感生电场[1]，和该处与变化电流的距离有关，总结实验结果可以得出电磁感应规律如下。

电磁感应规律：感生电场是顺着变化电流的——当电流变大时，变化电流在周围空间产生和变化电流反方向的感生电场，距离变化电流越近，感生电场越大;当电流变小时，变化电流在周围空间产生和变化电流同方向的感生电场，距离变化电流越远，感生电场越小。

此规律可延伸到电流距离变化时的“变化电流”[1]情况（有兴趣者可自己总结规律）。

2 麦克斯韦方程的不足

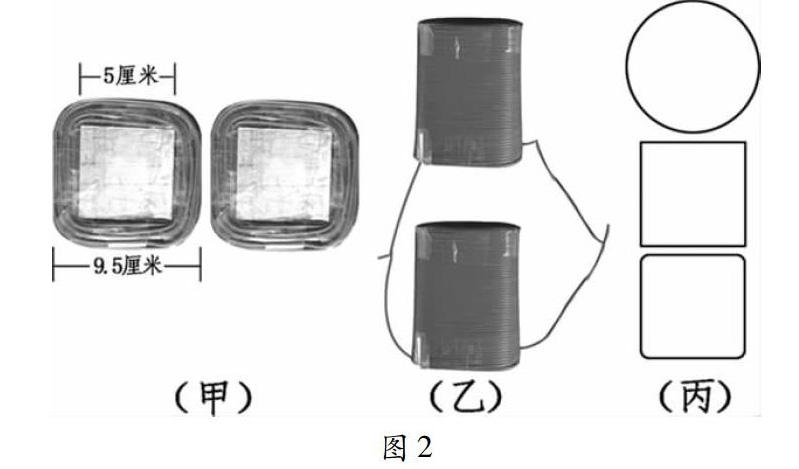
用电磁铁实验验证以上总结的电磁感应规律。仿照图1，用绝缘导线在两个截面为正方形的长方体铁块上密绕，正方形边长为5厘米，铁块长10厘米。在两个铁块上各密绕8层导线，密绕后形成2个电磁铁，图2（甲）为密绕导线后的两铁块之正方形面——正方形面加密绕导线后之平行边间的距离约为9.5厘米。参照图1，让这两个电磁铁上下平行摆放，两铁块之正方形面相邻，缠绕铁块的导线也仿照图1连接成两个端点用来连接电源，连接电源后两个电磁铁临近的两端一个是S极则另一个是N极，两个电磁铁距离5厘米，如图2（乙）所示。

下面做两组实验。

第一组实验：仿照图1，将同一根被感应导线在图2（乙）所示两个电磁铁中间分别围成直径约13.6厘米的圆形、边长约12厘米的正方形和此正方形的4个角改为圆角后的“新图形”，“新图形”形状较接近铁块密绕8层导线后之正方形面加导线后的形状，所围图形如图2（丙）所示，圆形面积略大于正方形面积，正方形面积略大于“新图形”面积，被感應导线分别围成以上图形后导线两端紧挨着射线状平行延伸远离两个电磁铁连接检流计形成闭合回路，所围图形的中心和两个铁块之正方形中心在同一条直线上，所围图形和铁块的正方形面平行。用1节1号干电池连接密绕铁块后连接成的两个导线端点，接通或者断开电源的瞬间，围成圆形时检流计指针最大摆幅约为4.6，围成正方形时约为4.6，围成“新图形”时约为4.9。

第二组实验：被感应导线分别围成直径为14.8厘米的圆形、边长为13厘米的正方形和此正方形4个角改为圆角后的“新图形”时，检流计指针最大摆幅分别为4.7、4.8和5.0。

用指南针做实验，实验显示两个电磁铁电流同时相同变化时被感应导线围成的图形其面积内的所有位置的磁场都是同向的，以上实验显示围成的面积变小后（“新图形”面积小于正方形面积和圆的面积）回路中产生的感应电流反而变大了，这个实验结果不符合法拉第电磁感应定律（ε=-ΔφΔt），也就不符合麦克斯韦方程。而这个实验结果是符合电磁感应规律所述“感生电场是顺着变化电流的”，“新图形”所围的面积最小而因其较接近导线所围形状，故产生的感应电流最大。本文是我写《变化电流产生感生电场》后进一步的实验和总结。

参考文献：

[1]赵继广.变化电流产生感生电场[J].科技风，2019（02）：248.

作者简介：赵继广，男，汉族，河北献县人，中国邮政集团有限公司保定市分公司（寄递事业部）职工。