浅谈向量在立体几何中的应用

2020-07-06陆俊玲

科技风 2020年18期

摘要：众所周知，立体几何在高中数学中有着举足轻重的地位，它对于学生逻辑思维和空间想象能力的培养和提高有着重要意义。利用空间向量可以解决所有的空间角与距离问题，并用代数的立式的形式对几何问题进行深入研究，并弥补了学生空间想象力的不足。文中简要地论述了高中立体几何教学中的困惑，并探讨了向量在高中立体几何中的重要作用，最后结合实例，感受向量在解题中的优势所在，旨在提升我国高中立体几何的教学水平。

关键词：向量;立体几何;应用

和传统的几何法相比，向量法的运用能够让学生在解答立体几何问题时变得更加快速、便捷，具有直觀、计算简单、以及不容易出错的特点。除此之外，向量作为高中数学中的重要组成部分，它能够采用数形结合以及坐标运算的方式快速解答各类几何问题，而且无需增加辅助线，让学生的答题过程变得更加轻松、高效。

一、向量在立体几何中的重要作用

向量能够把不同直线或者线段之间的几何关系运用直观的方式表现出来。由于向量的内容较为单一而且学习难度大，所以学生在进行向量学习的过程中要具有“数形结合”的思维意识，运用代数的方式来对几何图形进行描述。

（一）提高学生的运算水平

作为常用的代数对象，向量能够被运用到多种的运算模式中并且容易掌握，在提高学生解题效率和运算速度的过程中，还可以将原本复杂多变、解题难度大的几何问题用代数运算的方式进行直观地展示。

（二）具有重要的思维价值

向量既可以代数运算，又能够被运用到与度量相关的几何类问题，因此具有数形结合的特点。通过对向量的学习和运用，可以显著提高学生数学的学习兴趣，转变传统固态化的数学思维模式，提高自身的数学思维水平和空间理解能力。

二、向量法的解题方式与步骤

（一）向量法的解题方式

运用向量法解决立体几何问题主要有两种方式：即运用向量进行直接代数计算和利用向量坐标计算。在通常情况下是以坐标计算为主，因为这种计算方式所需要的计算技巧较少并且学生更容易理解和运用。值得注意的是，如果要解答的几何图形中确立坐标的难度系数较大，那么就可运用向量代数式的方法来进行解决。而后者解题时需要的解题时间较长而且解题的技巧更加复杂，对于学生的空间思维和逻辑运用能力也有着较高的要求。

（二）向量法的解题步骤

首先，在几何图形中构建空间直角坐标系。在这个过程中要尽量采用图形中已有的过同一点的两两垂直的线，若是未有三线也要想办法找出两线垂直的部分，接下来作出第三条线与之垂直;其次，把解题过程中将会使用到的坐标准记录下来。这个过程十分重要，一定要做到细致、认真，如果这一步没有处理好就会导致全题皆错的情况出现;再次，把解题过程中会使用到的向量坐标完整地记录下来，要运用终点坐标减去起始坐标;最后，利用记录下的坐标并运用代数计算的方式解决问题，这个过程中要保障公式的正确性，运算过程也要做到认真。

三、向量在立体几何中的具体应用

按照传统高中立体几何的教学模式来看，解决立体几何问题最为常用的方就是运用综合推理的方式。虽然这种方式可以在较快的时间内计算出结果，但是对于学生的空间想象和逻辑思维能力有一定的要求，既没有规律可以总结而且还有着较高的思维难度。而把向量引入到立体几何教学中，不但可以为解决高中立体几何问题带来了全新的思维模式和解决方法，而且还能够运用“数形结合”的方式，直观、具体地把立体几何里的“形”转变成为“数”来进行解决。

（一）线面计算

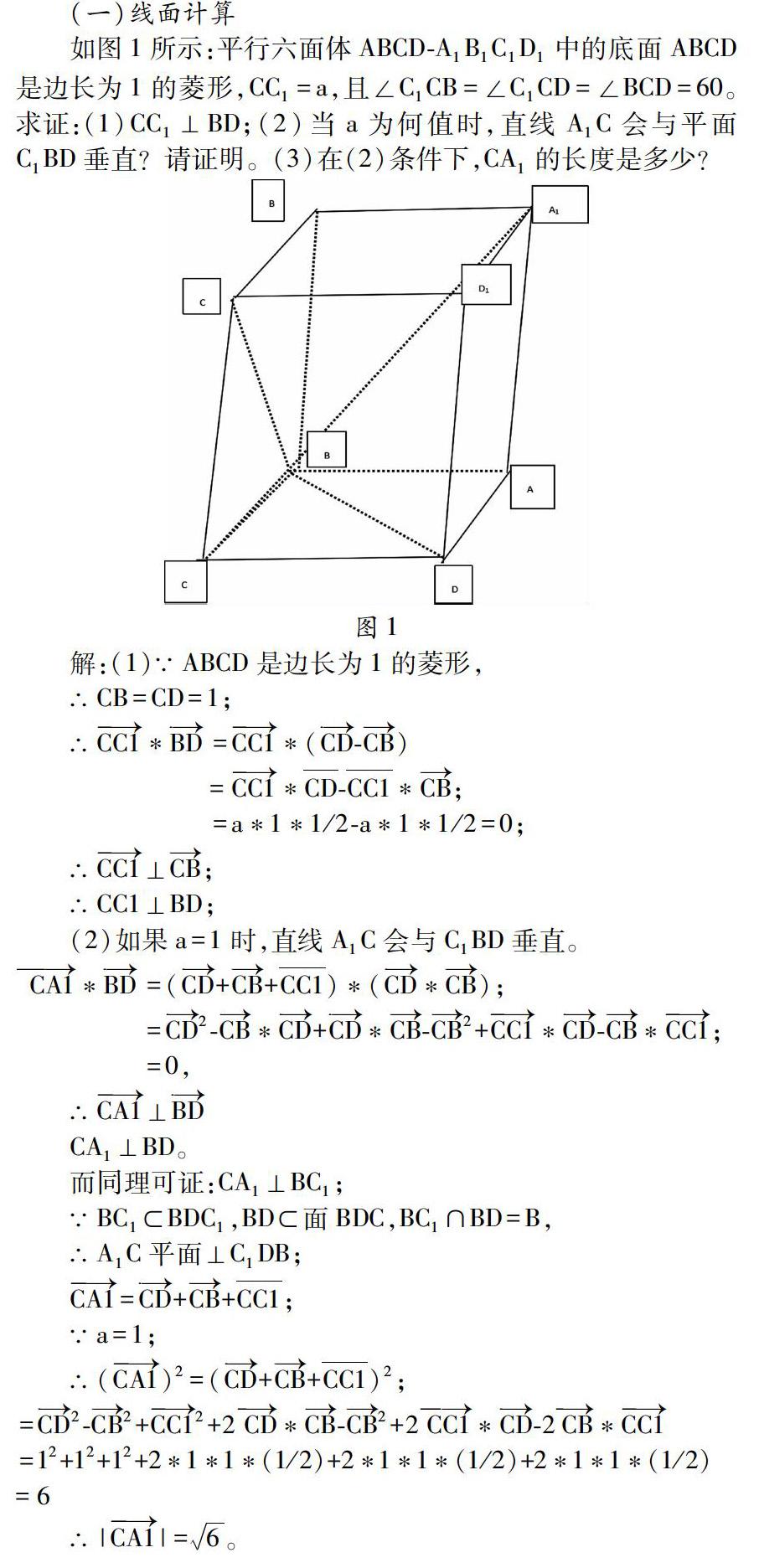
如图1所示：平行六面体ABCD-A1B1C1D1中的底面ABCD是边长为1的菱形，CC1=a，且∠C1CB=∠C1CD=∠BCD=60。求证：（1）CC1⊥BD;（2）当a为何值时，直线A1C会与平面C1BD垂直？请证明。（3）在（2）条件下，CA1的长度是多少？

（二）面面垂直运用

在高中的立体几何教学中，空间角部分的内容是整个立体几何教学的重点内容，而其中的两异面直线所形成的角更是其中的难点。如果运用传统的方式解决此类型的题目则会花费大量的时间，而且解题过程会变得复杂。而采用向量的数量积解决此类型的问题则效率更快，解题思过程也更加直观。

（1）求证：平面ADM⊥ABCM;

（2）是否存在满足BE=tBD（0

证明：（1）∵长方形ABCD里，AB=2AD=22，M是DC的中点，

三、结语

综上所述，在高中立体几何中运用向量法进行作答，既能够为广大高中生提供灵活的答题思路，还可以帮助学生摆脱传统立体几何的答题模式，能够运用直观的方式把立体几何问题中与“形”相关的问题转变成“数”模式，对于提高学生和答题准确性和答题效率具有重要意义。

参考文献：

[1]祝辉.空间向量在立体几何中的应用[J].上海中学数学，000（3）：41-43.

[2]黄亦飞.浅谈高中数学空间向量在立体几何中的应用[J].中华少年，2016（23）：171-172.