基于FR共轭梯度的SAR图像重构方法
2020-07-06周琦宾曾婷婷
周琦宾,吴 静,2,曾婷婷
(1.西南科技大学信息工程学院,四川 绵阳 621000;2.特殊环境机器人技术四川省重点实验室,四川 绵阳 621000)
0 引言
在各类成像雷达中,合成孔径雷达(synthetic aperture radar,SAR)具有分辨率高的特点。由于SAR的特殊成像原理,其不受一些外界条件(如温度与光照等)的影响,且发射的电磁波对云雨雾具有穿透性。因此,SAR的最大优点是全天候、全天时均可成像。因这一优点,SAR受到世界各国的重视,并且广泛应用于军事、民事等各个方面。受到奈奎斯特(Nyquist)采样定律的限制,出现了一系列新的问题,如:出于高分辨率与成本间的矛盾,SAR工作产生的大量数据难以得到快速处理;同时,也对硬件等提出了更高的要求[1-2]。所以,为了使SAR技术发展得更快,当前迫切需要在数据采集及信号处理等方面寻找更加合适的体制。
Donoho、Candes等于2004年提出压缩感知理论(compressed sensing,CS)[3]。其主要工作是对可压缩或稀疏信号进行压缩处理,并对相关非线性约束最优化问题进行求解,从而对信号进行近似重构或使其更加精确。在CS理论中,其非相关观测可以使SAR成像过程中需要的数据量得到降低。对于SAR系统需要的大量数据,CS理论有利于数据的采集、传输与储存等。
在压缩感知理论中,其关键问题是在重构模型的设计过程中,如何在保证性能优良的前提下使模型更加稳定。其中较为经典的是贪婪算法,主要包括正交匹配追踪[4](orthogonal matching pursuit,OMP)法与梯度追踪[5](gradient pursuit,GP)法等。这类算法计算量小,但重构精度不够高。除此之外,以线性规划为基础,另有梯度投影(gradient projection sparse reconstruction,GPSR)算法及基追踪[6](basis pursuit,BP)算法。与贪婪类算法相比,此类算法的特点是精度更高,但存在计算量较大、迭代速度慢等问题。2009年,Mohimani等首次提出了光滑L0范数(Smoothed L0 Norm,SL0)算法。该算法主要是将图像重构问题转化为凸优化问题,从而进行计算处理;采用拟合函数逼近离散的L0范数,通过优化算法实现问题的求解。该算法重构速度较快,重构精度更高并且对噪声具有一定的鲁棒性。本文基于SL0算法[7],进一步改进了与L0范数相近的拟合函数,同时对优化算法进行了改进,提出一种新的重构速度更快、重构精度更高的Fletcher-Reeves(FR)光滑零(FR Smoothed L0,FRSL0)压缩感知SAR图像重构方法。
1 SL0算法基础
基于L0范数的重构算法,其求解模型为:
(1)
式中:x为大小为N×1的稀疏信号[8];A为M×N(M≪N)的观测矩阵;y为信号x在观测矩阵下的低维投影。
在对近似L0范数进行估计时,关键问题是光滑连续函数的选择。光滑连函数用来拟合离散的L0范数,处理连续函数得到其最优解,从而得出L0范数的最优解。
在对L0范数进行估计时,SL0算法主要选择的是高斯函数,并且使用最速下降法与梯度投影原理[9]进行优化求解。高斯函数的表达式为:
(2)
由式(2)易推出:
(3)
式中:xi为稀疏系数x的分量;σ为参数。
若定义高斯函数族:
(4)
式中:N为稀疏向量s的元素个数;‖x‖0为向量中不为零的个数。
由式(3)、式(4)可知,x的L0范数可近似为:
(5)
由此可知, L0范数的最小化问题能转化为当σ→0时求Fσ(x)最大值。
2 基于FRSL0的SAR图像重构方法
2.1 函数的选择
在对L0范数进行近似时,SL0算法主要选择的是高斯函数。但该方法存在对L0范数拟合程度不高且计算复杂等缺点。文献[10]提出在对L0函数近似时,可以选择分式函数。分式函数的特点是较为简单,能够在保证不降低精度情况下,极大地减少迭代过程的计算复杂度与计算量。
分式函数表达式如下:
(6)
式中:δ为一个非常小的正数。
在进行迭代时,参数δ选择一组不断下降且无限接近于0的序列。显然,该函数满足:

2.2 基于FR共轭梯度的优化算法
SL0算法使用迭代计算近似得到L0范数最优解时,主要使用的是梯度投影原理以及最速下降法。但是采用最速下降方法进行最优问题求解时,搜索路径常常出现“锯齿形状”。该现象使得收敛过程困难、全局最优值较难得到,且很难估计其搜索路径。NSL0算法使用牛顿法计算更新迭代方向,可以使最速下降法中容易出现的“锯齿现象”得到抑制。但是在黑塞矩阵(Hessian matrix)的求解过程中,使用牛顿法的前提是保证矩阵的正定性。这就增加了计算的复杂程度。

本文将L0范数最小化问题等价转化为:
(7)
式中:λ为拉格朗日算子。
进一步由式(7)得:
(8)
式(8)为无约束的最优化问题,满足优化条件:

(9)

f′(x2),…,f′(xn)]T
(10)
式中:f′(x)为f(x)的导数。
当δ→0时,有:
(11)
为方便表示,令:

共轭梯度法的优点是避免了最速下降法的缺点,同时也解决了牛顿法中局部收敛性以及复杂的计算问题。此外,该算法并不需要计算黑塞矩阵,并且具有稳定性较高且所需内存量较小等特点。针对式(11),其最优化问题如下:
(12)
4FRSL0的算法步骤如下。
初始化:设定初值x0=AT(AAT)-1y,置迭代步数j,选择合适的递减序列[δ1,δ2,..,δj]。
迭代寻优:
forj=1,2,…,j
(1)δ=δi。

fork=1,2,…,L
①求可行下降方向:

其中,αk由FR公式得到:

②利用梯度投影法,对可行方向进行求解:
d(k)=(I-AT(AAT)A)d(k-1)
利用精确一维搜索,对步长μ进行计算确定。令:
X(k)=X(k-1)+μd(k)
3 试验结果及分析
对三幅SAR图像,采用不同算法的重构性能参数如表1所示。
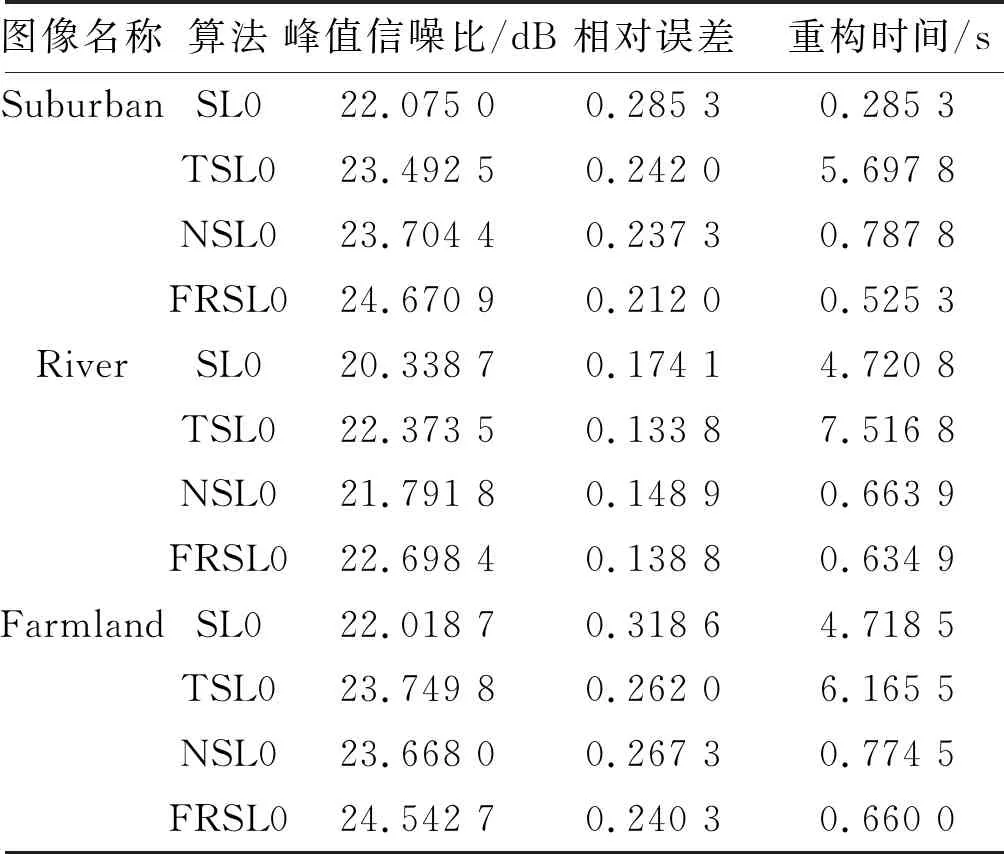
表1 不同算法的重构性能参数
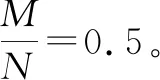
不同算法对图像Suburb重构效果对比如图1所示。

图1 不同算法对图像Suburb重构效果对比图
不同算法对图像River的重构效果对比如图2所示。

图2 不同算法对图像River的重构效果比较图
不同算法对图像Farmland重构效果对比如图3所示。

图3 不同算法对图像Farmland的重构效果对比图
从试验结果可以看出,对比三幅SAR图像的重构效果,本文选择的算法提高了重构的精度、质量。结合表1可知:重构效果较差的是SL0算法;与NSL0算法相比,FRSL0算法略胜一筹。在对所有图像的试验中,经过本文算法的重构图像峰值信噪比值较高,重构相对误差最低,可见本文算法具有一定的鲁棒性,且对不同类型图像重构都具有一定优势。而从图1~图3能够看出,本文算法重构的图像更清晰、出现的瑕疵和噪点更少。因此,本文算法重构效果更好。
图4与图5分别给出在不同压缩比下,四种算法的峰值信噪比与运行时间的性能比较曲线。从图4中可以看出,本文算法在不同压缩比下峰值信噪比值均略高于其他算法。图5中,在不同压缩比下,本文算法的运行时间与NSL0算法运行时间曲线略有重合,当压缩比超过0.5时,运行时间也随之增加。
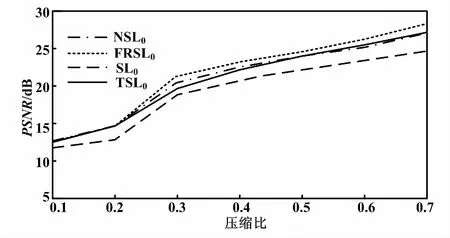
图4 不同算法性能对比曲线(PSNR)

图5 不同算法性能对比曲线(运行时间)
4 结论
本文以压缩感知理论为基础,基于对SL0算法的深入研究,使用一个较为简单的分式函拟合L0范数,得到一个新的优化问题。通过对牛顿法及最速下降法的优缺点进行比较分析,提出一种使用FR共轭梯度
法进行迭代寻优的SAR图像重构方法。在FRSL0算法中,只需计算一阶导数。这样既可避免最速下降法中慢收敛性的缺点,又可避免牛顿法中因求解黑塞矩阵导致计算复杂的缺点。仿真试验表明,与现有的典型算法相比,在以L0范数为基础的重构算法中,本文算法重构的效果十分优良。
