基于非参数回归的航材消耗预测模型研究
2020-07-06陈振林薛永亮
陈振林,薛永亮
(海军航空大学 岸防兵学院, 山东 烟台 264001)
关于航材的预测,国内外学者采用了多种方法进行试验拟合,其中包括线性回归、神经网络、支持向量机等方法[1-5]。线性回归模型对缺少明确变化趋势、离散型数据拟合较差,但其算法固定,通过规定的算法得出唯一结果,且其延伸性能较好;支持向量机是一种优秀的机器学习预测算法,能较好解决局部最优、过度学习等问题,对小样本信息预测效果较好,但其对于较大步幅预测,由于缺少样本支撑,经常拟合效果较差。
对某型引俄直升机航材消耗建立模型时,需要考虑两个特点:一是机型较新、服役时间短,难以获取足够数据,不能划分训练集;二是机型备件国产化水平低,大部分要依靠进口,补给难度较大且易受多种因素影响,对该机型航材消耗,不仅要预测T+1时刻,还要预测T之后较长步幅的区间。基于上述问题,本文使用非参数回归算法建立模型。非参数回归是一种不对模型参数做任何假设的回归算法[6],仅规定一些一般性条件,近年来该算法在多学科运用较为广泛[7-13]。
1 非参数回归分析
回归分析是应用最广的统计分析方法,其一般模型数学表达式为:
Y=m(X)+U
(1)
式(1)中:X预测变量;Y是X的响应变量;U是随机误差,且满足E(U|X)=0,E(U2|X)=σ2(X);m(·)是光滑函数[14]。若m(·)模型已知,参数未知即为参数回归。对于模型的估计,需要一定的先验知识做出强假设,否则会有较大偏差。当m(·)模型未知,该回归函数即为非参数回归,在分析时不做任何参数假定。
对该型直升机,预测时可以根据相似机型基础上修正,计算出足够量的先验知识,利用贝叶斯大数定律预测[15-17]。但是类比推测的过程中不可避免会产生误差,并且使用参数回归形式一旦固定,经常拟合效果差。在这种情况下,当数据样本容量足够,使用非参数回归具有一定的可行性,且应用范围更广,性能更稳健[18]。使用非参数回归建模,不需要对数据样本做先验估计,仅依靠数据自身规律进行拟合,通过每个数据计算权重,使得回归曲线具有整体性,对长步幅区间的预测效果较好[6],能较好解决该机型样本数据少、预测长区间等问题。
非参数回归有多种算法,最经典的是局部核回归,对m(·)估计的数学表达式为:
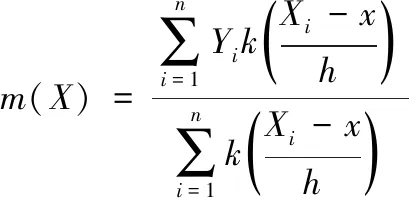
(2)
式(2)中:k(·)是核函数;h是带宽;Xi、Yi分别为预测变量与响应变量。如式(2)所示,平滑函数仅与X、Y相关,通过选取适当的核函数与带宽,建立预测模型。
2 基于非参数回归的航材消耗预测
2.1 航材消耗序列
选取某型引俄直升机一种关键航材,统计8年的航材消耗数据。在8年时间内,该型飞机由于各种原因服役数量存在波动,在本文中,转换为单机月平均消耗件数,方便预测模型的建立。其消耗序列如图1所示,可以初步看出,消耗序列较为离散,有缓慢上升趋势。利用非参数回归模型,对数据样本不做先验假设,依据数据样本自身特点进行回归运算。
2.2 局部多项式回归算法
局部核回归存在边界带估计偏差较大的缺点,对其回归算法进行改进,建立局部多项式回归[7]。其主要方法是在x的一个邻域内,用多阶多项式去估计光滑函数m(·),然后进行核函数加权,求出m(·)及各阶系数。p阶局部多项式估计是求下式最小值的解,即:
(3)
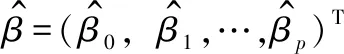
(4)
Y=(Y1,Y2,…,Yn)′
(5)
β=(β0,β1,…,βp)′
(6)
(7)
将式(3)转化为:
M=(Y-Xxβ)TWx(Y-Xxβ)
(8)
即转化为求式(4)的最小二乘问题。
取p=1,有:
(9)
经计算可得
(10)

图1 航材消耗序列图
2.3 模型选择
核函数有多种选择,通常有Triangle、Epanechnikov、Quartic、Triweight、Gaussian等核函数,有学者指出当带宽h合适时,核函数的选择对于回归结果影响较小[20-22]。针对上述数据较为离散、变化趋势不明显的问题,使用高次方函数精确性会有一定提高[23],使用Triweight函数作为备选函数,其数学表达式为:
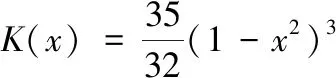
(11)
在试验中发现,使用Triweight核函数,在序列两端偏差较大,高次幂对权重影响较大,对该核函数改造为:
K(x)=(1-3x2+0.5x4)(1-0.2x2)
(12)
由此能有效降低高次幂在两端的影响,一定程度消除偏差。
对于带宽h的选择优化问题,有了较多的研究,较多学者使用交叉验证选取[20-24]。交叉验证是通过构建均方误差最小的估计量来确定最优带宽,通过剩余数据量来预测响应变量,但对于预测外延有一定误差,本文使用经典拇指法则[6],其数学表达式为:
h=1.06σn-0.2
(13)
式(13)中:σ为样本方差;n为样本个数。
3 仿真实验
为有效对比非参数回归模型准确性,使用多种方法对消耗数据进行建模。使用前72个数据建立模型,预测73-84数据,与真实数据做对比。
3.1 数据检验
数据检验是回归建模的基础工作,对数据的平稳性做出检验,若不满足要求,在回归拟合前需要进行偏差处理。使用Eviews进行单位根检验,检验结果如图2所示。
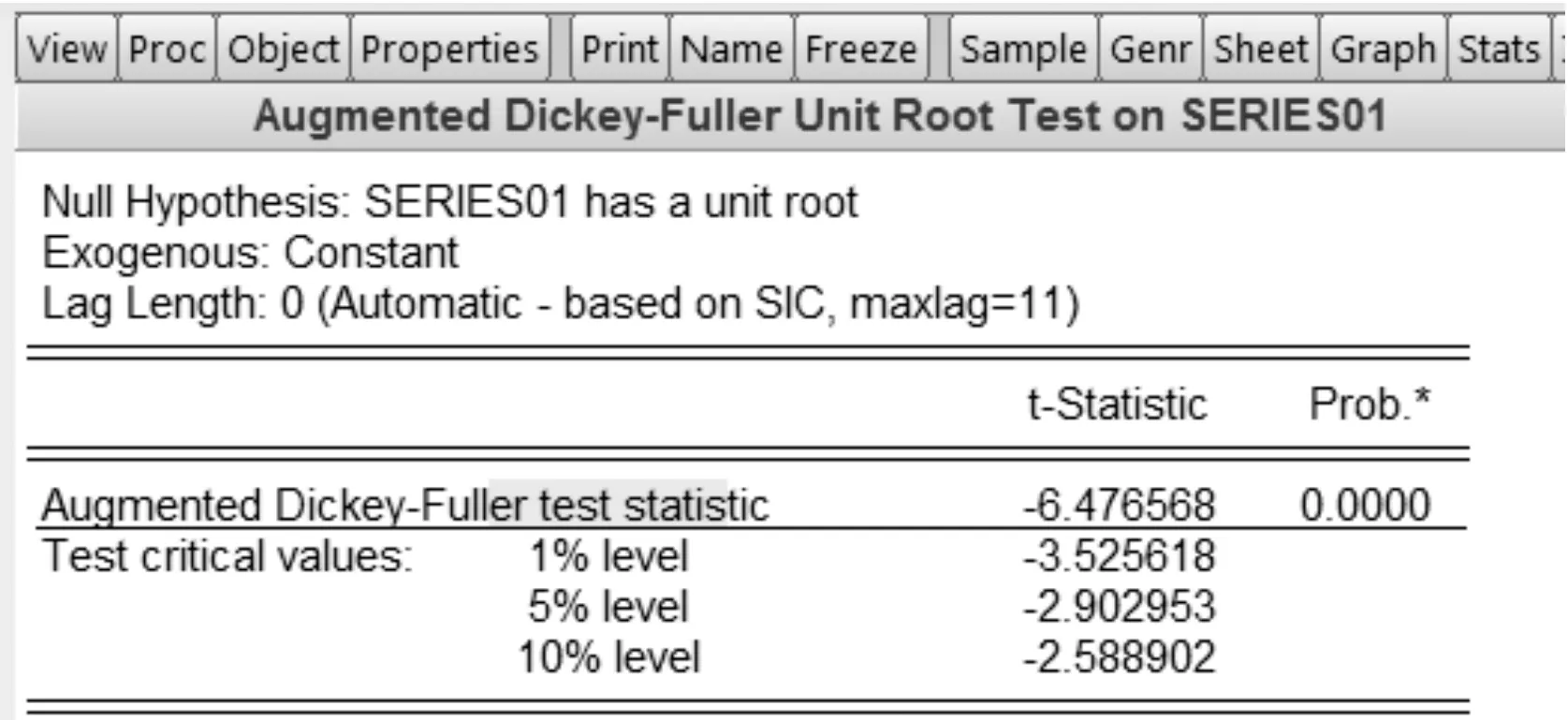
图2 平稳性检验结果
通过ADF(Augmented Dickey-Fuller)检验T值满足要求显著性检验,P值为0,认为消耗序列平稳,无需进行差分运算[15]。
3.2 试验对比
分别使用最小二乘法 (Least Square Method)2阶、3阶、4阶,自回归滑动平均模型(Autoregressive Moving Average Model)、非参数回归(Non-parametric Regression)等方法建模,仿真曲线如图3所示。
由图3可以看出,自回归滑动平均模型对于长步距预测效果较差,最小二乘法拟合曲线由于序列自身波动性较大而缺少明显趋势,拟合过于平滑,但3阶算法预测结果与实际消耗趋势相同。非参数回归由于两端高次幂影响偏差较大,通过改进后模型有了较好优化,曲线拟合与实际消耗情况相近。
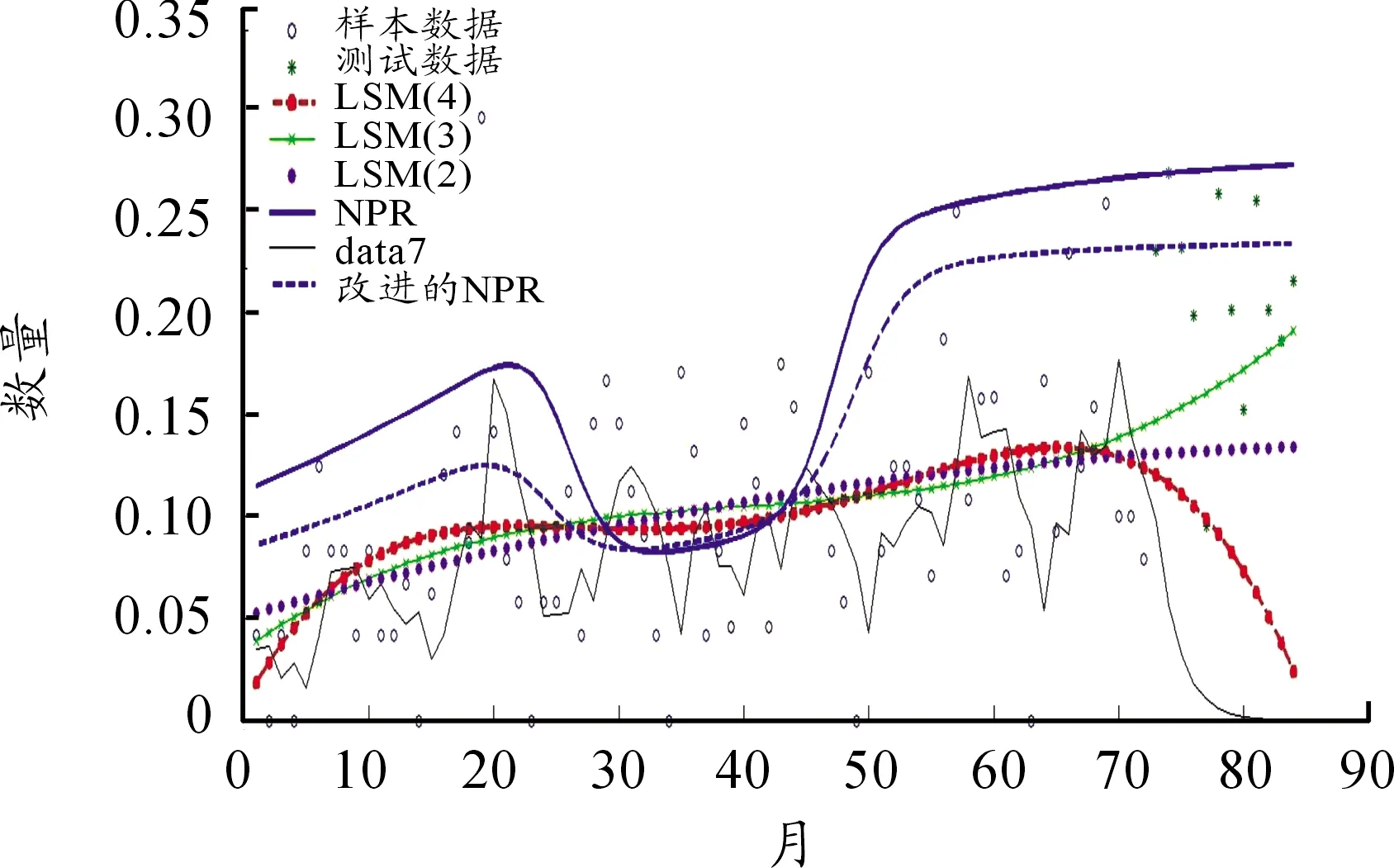
图3 回归仿真曲线
支持向量机(Support Vector Machine)对小样本预测较为理想,多名学者在此基础上进行了改进,取得了一定的成果[25]。为充分对比,本文使用SVM对上述仿真进行建模。在上文建模仿真中,73至84数据设为未知,因此在设计SVM试验时,设置[1,60]数据为训练集、[61,72]数据为标准集,对[61-84]数据预测拟合,其推导原理及试验过程在此不做描述,仿真结果如图4所示。

图4 SVM仿真曲线
由图4可以看出,由于前期数据支撑,对于近邻阶段预测效果较好,61~72仿真数据拟合较为理想,对比回归曲线更加接近数据样本。但74之后数据拟合效果较差,对于消耗数据上升趋势未做有效预测分析。
为有效评价模型拟合效果,使用以下两个指标分析对比不同模型的预测准确性。
1) 均值百分比误差MAPE。其数学表达式为[10]:
(14)
2) 均方根差RMSE。其数学表达式为[10]:
(15)
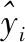
对其后12项数据预测结果如表1所示。由表1可以看出,最小二乘3阶模型与非参数局部多项式回归预测效果接近,而改进后非参数局部多项式回归预测效果明显较好。

表1 预测效果对比
4 结论
基于非参数回归算法建立航材消耗预测模型,在建模时不对变量作强假设推定,通过样本数据自身进行拟合,使得模型具有自适应性。利用局部多项式回归算法建立模型,并根据数据特点修正模型,仿真实验表明,对于多种回归算法,基于非参数回归的航材消耗预测模型拟合效果更好、预测误差更小,具有较高的准确性。
