基于成本指数的民机四维航迹预测优化算法

2020-07-06樊刘仡郑智明

民用飞机设计与研究 2020年2期

樊刘仡郑智明薛飞王青

(上海飞机设计研究院，上海 201210)

0 引言

随着社会经济的快速发展，空中交通运输需求与日俱增，空域拥堵、航班延误等问题日益严重，给民航安全、高效运行带来了严峻的压力。为了应对目前空中交通运输上存在的问题，国际民航组织提出了全球空中交通管理运行战略[1-3]。该战略指导未来空中交通管制从基于指令运行(Command-Based Operation，简称CBO)向基于轨迹运行(Trajectory-Based Operation，简称TBO)转变，而基于轨迹运行的理念在时间与空间上对航空器飞行轨迹的预测提出了更高精度的要求。

轨迹预测是按照飞行计划中的控制方案驱动飞机性能模型进行飞行全过程的快速数值仿真[4]。它不仅能够计算得到飞机飞行的三维轨迹，而且能够预测出飞机在飞行轨迹上每一点的时间、空速、地速、质量、油耗、升力和阻力等全状态信息，得到飞行全过程的高维预测数据。为减少空气污染，节省燃料消耗，除了在飞机设计阶段采取多种优化技术以外，也可以在运营阶段利用FMS计算最优高度速度计划表和最优轨迹对飞机的性能进行优化[5-6]。

优化参考轨迹主要有两种手段，一是考虑飞行器运动方程(Equation of Motion，简称EOM)，用最优控制的方法来得到最优轨迹[7-8]；二是动态查询性能数据库[9-10]，考虑在风或者高度变化因素影响下的性能优化问题。由于FMS计算效率不高，难以使用EOM进行大量实时运算，因此通常使用查询性能数据库(Performance Database，简称PDB)中的经验表格的方法来完成计算。PDB中的数据以离散形式存储，因此可以将轨迹优化问题视为一个组合优化问题。对于优化指标的选择一般有燃油消耗和飞行时间两种，飞行成本指数能够对两者进行有效的权衡，因此本文提出了一种基于成本指数的方法对民用飞机的四维航迹预测进行优化。

1 成本指数与代价函数

飞行成本是飞行航迹优化过程中必须考虑的关键指标。一般来说，飞行成本可以分为固定成本和变动成本。其中固定成本在一定范围内与航空公司业务量变化关系不大，譬如发动机大修费用、机组固定工资、月固定租赁费用、飞行训练费用等。变动成本包括燃油成本和其他与飞行时间相关的成本(以下称为时间成本)，譬如机组的小时薪水提成、小时租赁费用、飞机维护成本等。

飞行航迹的优化通常只考虑变动成本，即燃油成本和时间成本，而不将固定成本考虑在内。记单位燃油成本为Cf元/kg，单位时间成本为Ct元/min，则可以定义成本指数(Cost Index，简称CI)为：

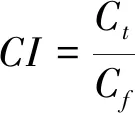
(1)

单位为：kg/min。

成本指数一般由机组人员在飞机起飞前通过显示控制系统的人机界面输入到飞行管理计算机中。成本指数的取值反映了时间成本和燃油成本在飞行总成本中的构成比例。当成本指数为0时，表征时间成本可以忽略不计，飞行成本的全部权重集中于燃油成本，此时优化的结果为最省油的飞行模式，即最大燃油里程模式。当成本指数取最大值时，表征燃油成本可以忽略不计，飞行成本的全部权重集中于时间成本，此时优化的结果为最短飞行时间。一般来说，按照最大燃油里程模式飞行速度太慢。当飞机处于最大燃油里程状态飞行时，以多消耗1%燃油为代价就可以换取3%～5%的速度提升。因此，在实际工程中，一般不会将成本指数设为0。同理，也不会将成本指数设为最大值。对于不同的飞机和不同的航空公司，成本指数的取值范围也会有很大差别。以波音系列飞机为例，表1展示了部分型号飞机飞行过程中选用的成本指数的范围。

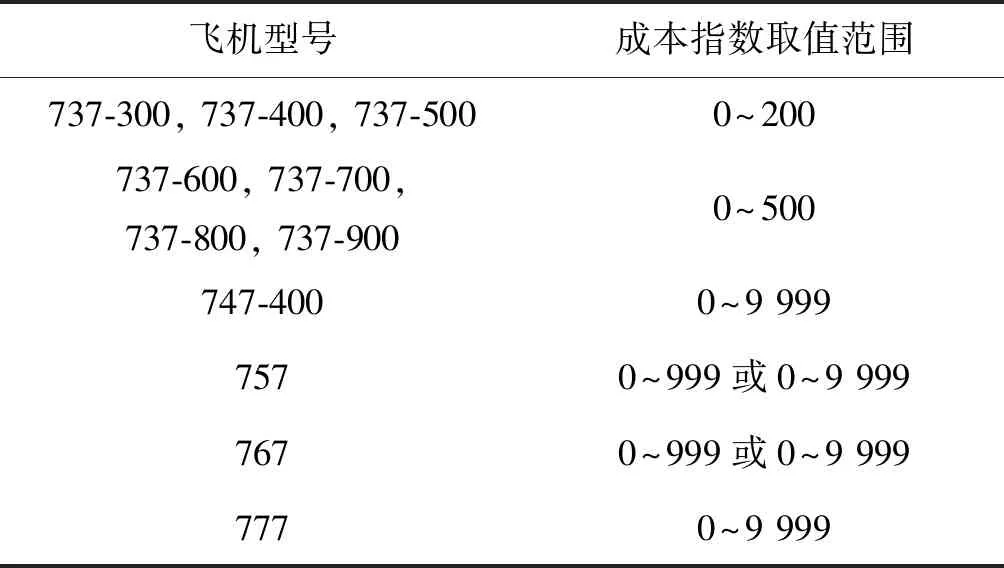
表1 波音系列飞机成本指数取值范围

在实际运行过程中，通常会将成本指数设置为两者之间较为合适的值。表2显示了波音系列飞机成本指数推荐的取值。

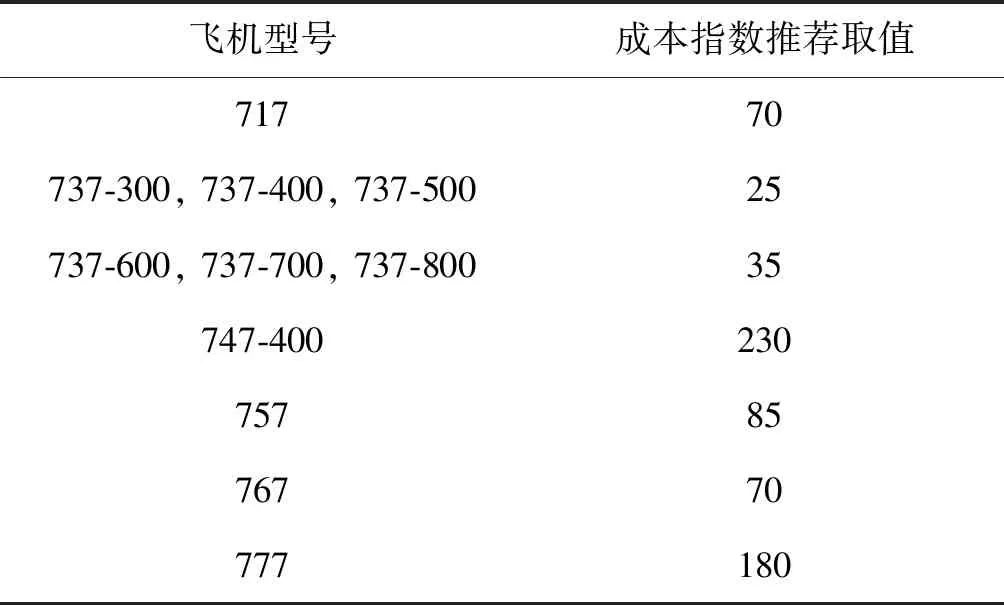
表2 波音系列飞机成本指数推荐取值

通过成本指数，可以计算飞行的直接运行成本(Direct Operating Cost, 简称DOC)：

(2)

其中,t0为起飞时刻，tf为降落时刻，f为燃油流量(单位时间内消耗的燃油量)。

飞行成本的变化与巡航速度的选取有密切的关系，如图1所示。时间成本随巡航速度的增大而递减，燃油成本随巡航速度的变化会出现极小值，极小值处取得最大燃油里程速度。当速度小于最大燃油里程速度时，燃油成本随巡航速度增大而减小；当速度大于最大燃油里程速度时，燃油成本随巡航速度增大而增大。总成本随巡航速度的变化也会出现极小值，极小值处取得最经济巡航速度。

成本指数对垂直剖面的影响如图2所示。成本指数增加会导致爬升顶点和下降顶点在水平方向上的投影均向前运动。

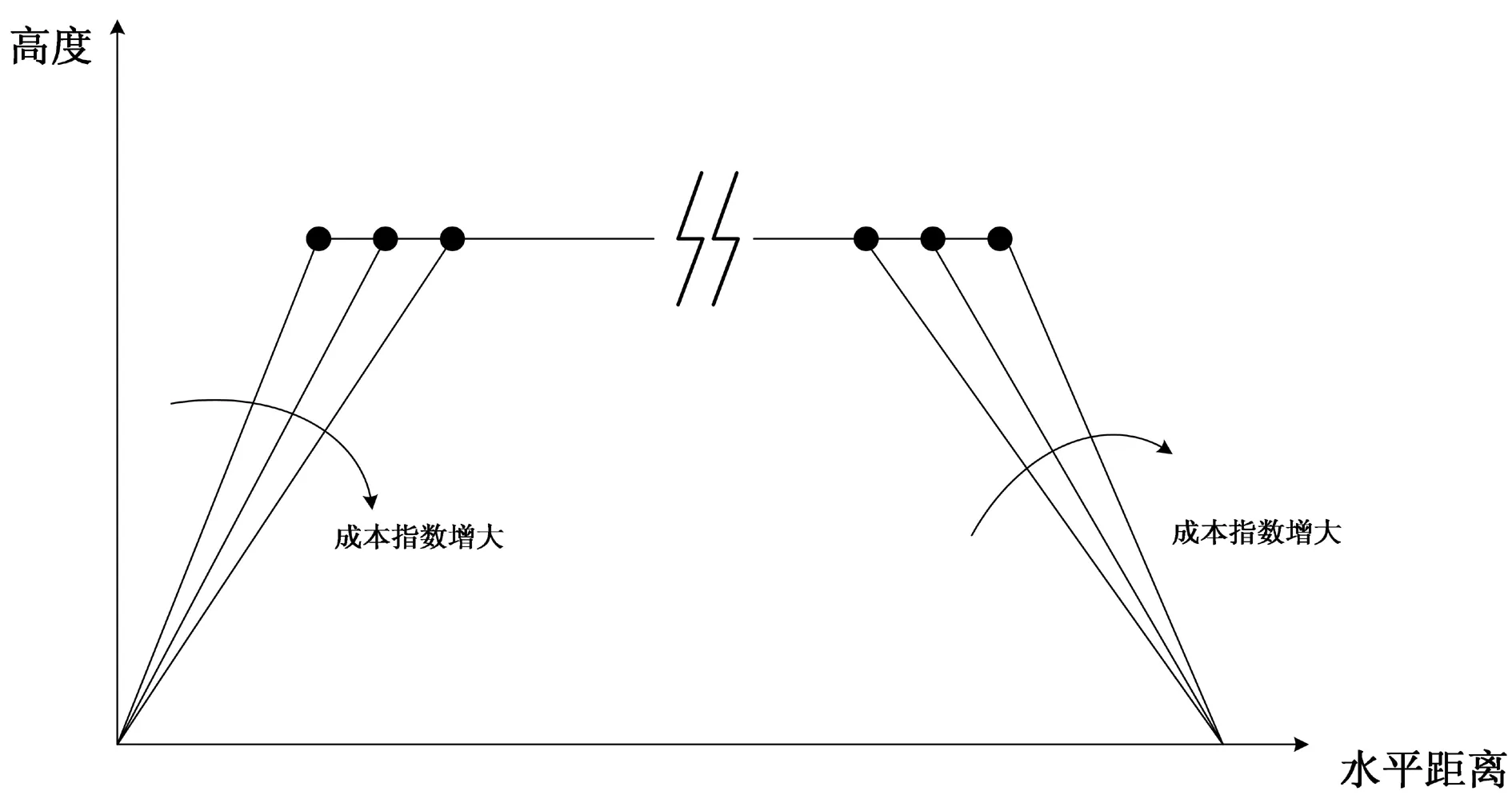
图2 成本指数变化对上升顶点和下降顶点位置的影响

针对轨迹优化需要定下优化的目标，即获取计算航程代价的函数，根据需求的不同，航程代价一般指航行中的燃油消耗、时间、成本指数CI的综合代价。

定义航程成本如式(3)所示：

Cost=FBurned+CI×TFlight

(3)

其中，FBurned是总航程的燃油消耗，单位kg，TFlight是总航程时间，单位min，CI是成本指数，单位kg/min。CI一般由运营方提供，CI越高，表明时间成本比重越高。

2 四维航迹优化方法

根据ARINC702A中关于性能计算模块的规定，机载性能数据库主要由以下三个方面组成:

1)飞机气动模型数据库，内容包括升力系数、阻力极曲线等飞机气动外形数据；

2)发动机数据库，主要由发动机推力模型和耗油特性数据组成，内容包括发动机推力模式、推力限制、推力使用状态以及对应的耗油特性等数据。

3)空中性能数据库，内容包括飞机在起飞、爬升、巡航、下降和着陆阶段等飞行模态下的速度、燃油消耗、时间、水平距离和重量等数据。同时还包括基于性能数据二次计算得到的与航路相关的性能数据，以便机载性能管理。

飞机性能手册中提供的数据包含曲线和表格两种形式，将数据整理构建成便于系统调用的数据库，涵盖飞行包线数据、发动机数据和空中性能数据三个方面以供FMC调用。由于很多数据是离散存储的，因此可以使用插值方法进行制备和查询。

为了寻找最优的轨迹，需要计算按照不同速度高度计划表飞行的航程代价并进行比较，如果采取巡航阶段阶梯爬升，也需要计算爬升所带来的额外代价。最后，利用穷举的办法，计算所有可行的轨迹，选择总航程代价最低者作为最优的垂直剖面。

根据第1节的描述，以航程代价最小为目标时，轨迹优化的主要环节在巡航阶段，可以用基于成本指数的方法进行优化。

3 最经济巡航速度的计算

飞机在巡航阶段飞行时，高度变化量近似为0，速度变化量近似为0，巡航过程中迎角很小，α也可近似视为0。在飞机水平航迹确定的情况下，其在垂直剖面内的运动可以近似用质心运动方程来描述：

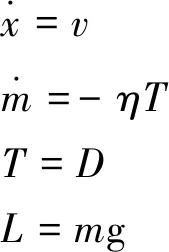
(4)

其中，x为飞机在水平方向上的位置，v为飞行真空速，T为发动机推力，D为阻力，L为飞机升力，m为飞机质量，g为重力加速度，η为推力单位燃料消耗。

根据第2节对飞机性能模型的描述，可以得到如下关系：

在垂直剖面的优化过程中，优化目标是飞行总成本：

其中，F为总燃油消耗量，f为燃油流量，t为飞行时间，CI为成本指数，Cf为燃油价格，Ct为单位时间成本，η为推力单位燃料消耗，D为飞机阻力。在优化过程中给定了初始飞行时刻t0，初始飞机重量m0，初始位置x0。

考虑到燃油价格Cf是给定的值，因此优化目标可以写成：

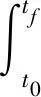
s.t.

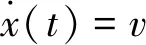
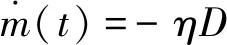
x(t0)=x0,x(tf)=xf,m(t0)=m0,h(t)=h0

(7)

取v为优化变量，使用HJB方程求解上述优化问题，得到最经济巡航速度v*，并通过仿真的方法作出v*随巡航高度的变化关系如图3所示。图中，各条曲线代表不同成本指数下的情况，巡航重量取240 t，成本指数变化范围取0～100，每间隔10取一个样本点；横坐标代表巡航高度，变化范围取0 m～12 000 m，每隔100 m取一个样本点；纵坐标代表计算得到的最经济巡航速度。

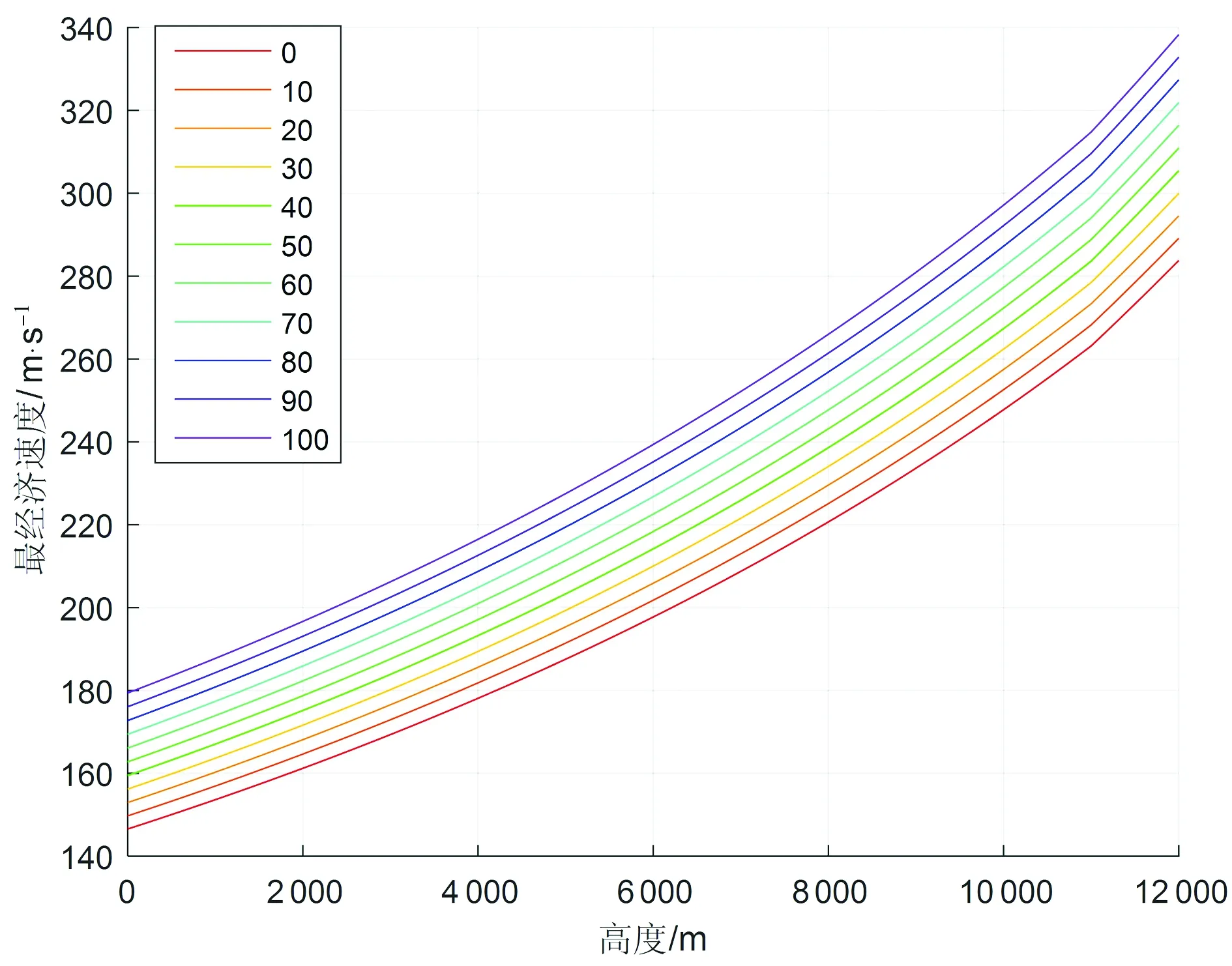
图3 最经济巡航速度随高度的变化关系示意图(不同成本指数下)

从图中可以看出，当巡航高度在7 000 m～11 000 m范围内变化时，计算出的最经济巡航速度与高度呈现近似线性关系。当高度达到对流层顶后，温度不再随高度增加而变化，因此图像上曲线斜率在该点处发生改变，如图4所示。

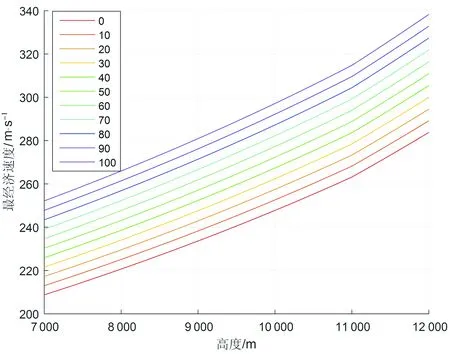
图4 最经济巡航速度随高度的变化关系示意图(7 000 m～12 000 m段)

由于v*与h之间存在局部近似线性关系，因此可以利用最小二乘的方法拟合曲线斜率。这样，只要知道了给定成本指数下某一巡航高度对应的最经济巡航速度，很快就能通过拟合公式计算其他高度对应的最经济巡航速度。

4 最经济巡航高度的计算

类似的，以巡航高度为优化变量，使用HJB方程求解上述优化问题，发现在巡航速度确定后，巡航高度越高，巡航总成本越小。因此对于高度的优化需要利用飞行包线的限制。

受飞机性能和空中交通管制约束，民航飞机只能在一定的飞行包线内飞行。以波音747飞机为例，其巡航马赫数限制不能超过0.89 Ma，巡航高度不能高于45 000 ft。取最大巡航马赫数为0.85 Ma, 假设巡航高度变化范围为7 000 m～12 000 m。飞机在某个巡航高度上飞行时，速度不能无限增大。加速过程中，当最大推力等于阻力时，飞机达到最大速度。类似地，飞机飞行高度也不能无限增大。随着飞行高度的增大，发动机最大推力减小，直到不足以克服飞行受到的阻力，飞机的飞行高度下降。

根据飞机性能模型，有：

其中，ΔTeff=ΔT-CTc,4,0≤ΔTeff·CTc,5≤0.4,CTc,5≥0,CTc,3=0,CFcr=0.966。

又：

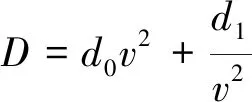
(9)

其中，

令最大巡航推力等于阻力，

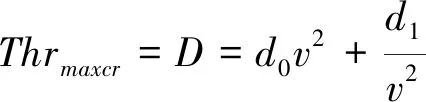
(11)

则：

解得：

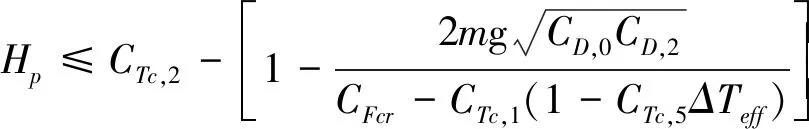
(13)

此即为最大巡航高度的约束条件，发现其与飞机巡航重量相关。飞机巡航重量减小时，最大巡航高度会随之增大。对于起飞重量250 t的情况，可以计算最大巡航高度约为10 700 m，约合35 000 ft。

下面讨论在固定飞行高度的情况下巡航速度的约束条件,可得：

在巡航重量240 t的条件下，改变巡航高度，可以得到速度约束如图5所示。

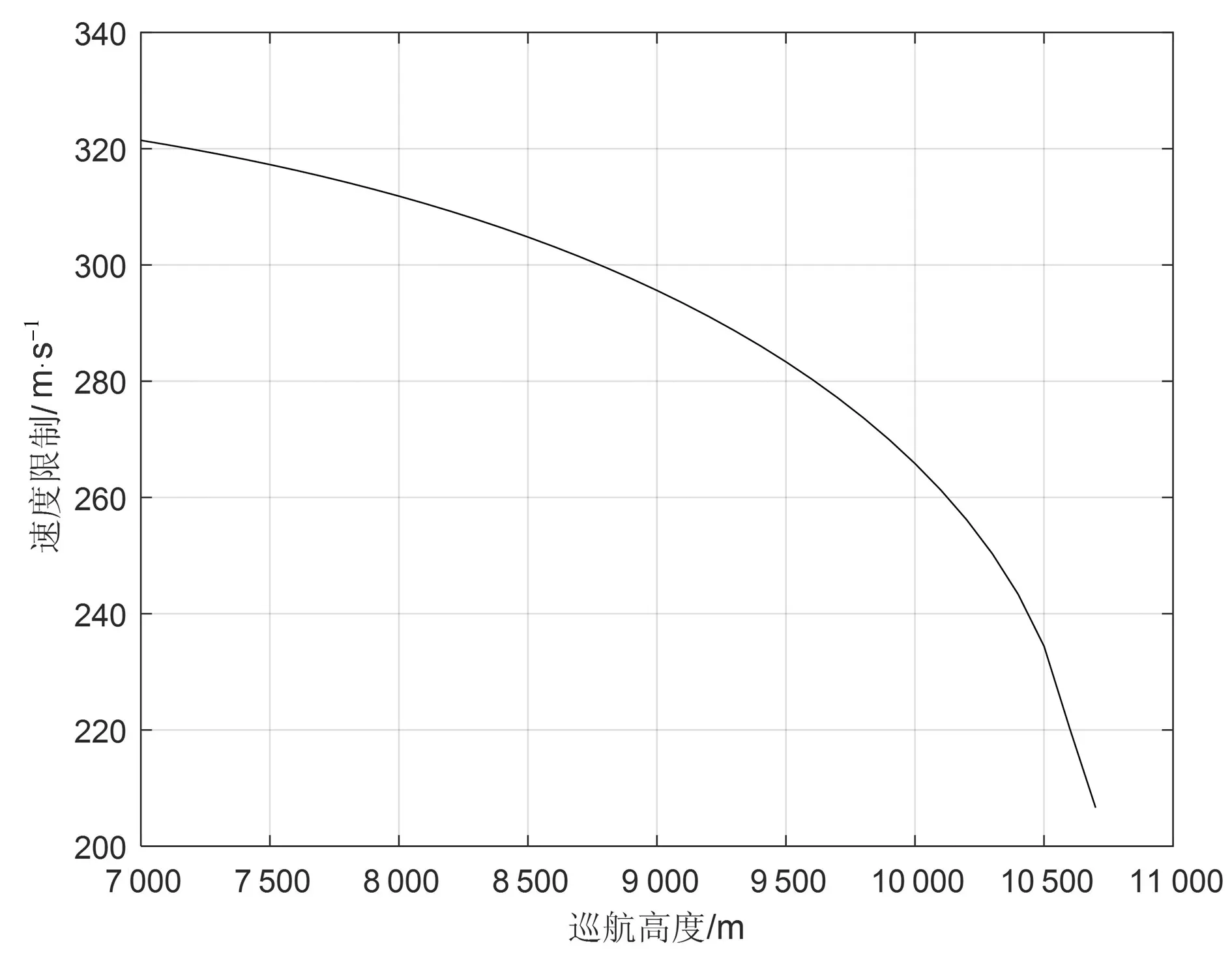
图5 最大巡航速度随巡航高度变化曲线(推力约束下)

可见随着巡航高度的增大，最大巡航速度限值随之减小。取速度最大限值时飞行总成本的变化曲线如图6所示，其中巡航高度变化范围为10 000 m～10 600 m，每隔100 m取一个样本点，成本指数取为30。发现在发动机最大推力约束下，总成本随巡航高度的增大呈现出先减小后增大的变化趋势。

考虑0.85 Ma的最大巡航马赫数限值。固定巡航速度为0.85 Ma，改变巡航高度，从7 000 m～10 000 m，每隔500 m取一个样本点。得到飞行总成本随巡航高度的变化曲线如图7所示。在最大巡航马赫数的条件下，随着巡航高度的增大，飞行总成本逐渐减小。

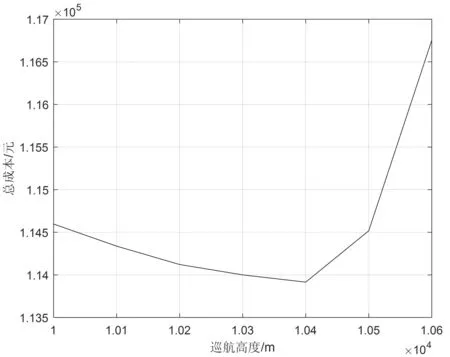
图6 取速度最大限值时飞行总成本随巡航高度变化曲线(推力约束下)

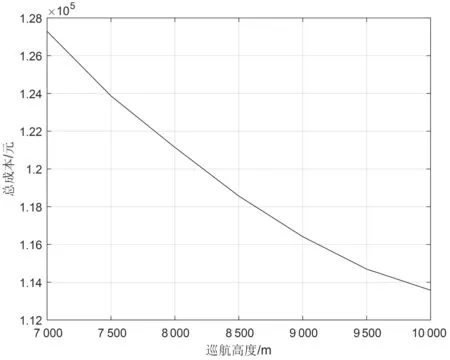
图7 飞行总成本随巡航高度变化曲线(最大巡航马赫数约束下)

综合以上分析，可以得到最经济巡航高度的求解方法，如图8所示。

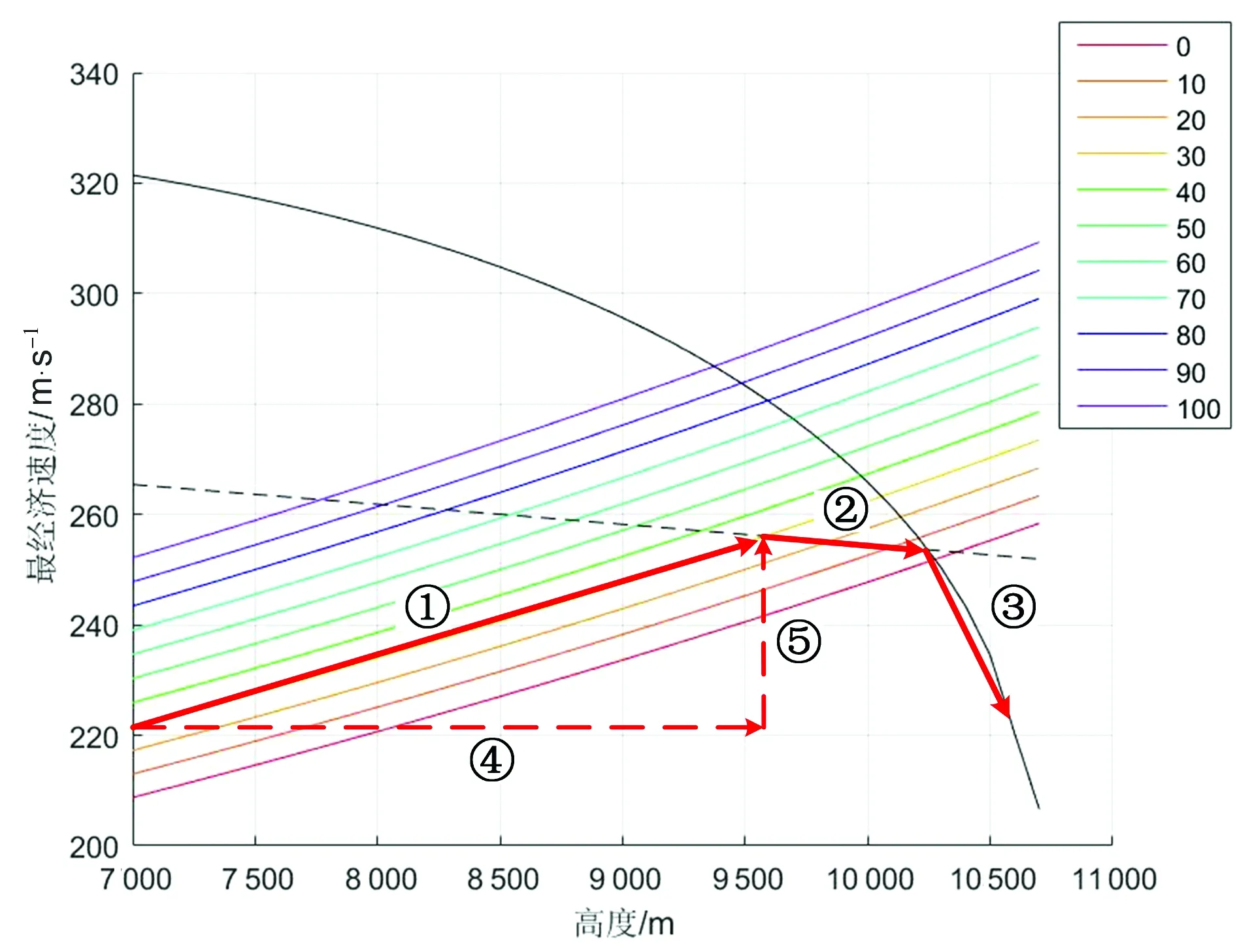
图8 最经济巡航高度求解示意图

其中一族平行的直线表示不同成本指数下最经济巡航速度随巡航高度的变化情况；黑色虚线表示最大巡航马赫数的限制，本文中取0.85 Ma；黑色实线表示发动机最大推力对巡航速度的限制。

以成本指数CI取30，起飞重量取250 t的情况为例进行分析。图8中①过程可以分解为④过程加⑤过程。在④过程中巡航速度不变，巡航时间成本近似不变，当巡航高度增大时，由于大气密度下降，阻力减小，因此燃油消耗减少，燃油成本降低，导致飞行总成本降低；在⑤过程中，由于是在高度不变的情况下向最经济巡航速度的方向变化，因此飞行总成本会降低。综合对④、⑤过程的分析，可知①过程中飞行总成本是单调下降的，即随着巡航高度的增加，最经济巡航速度对应的飞行总成本单调递减。②过程沿着最大巡航马赫数限制线变化，根据图7的实验结果知，当巡航高度增加时，飞行总成本呈现下降趋势。③过程沿着发动机最大推力限制线变化，根据图6的实验结果知，当巡航高度增加时，飞行总成本呈现先减小后增大的变化趋势。

根据对①、②、③过程的分析可知，在成本指数为30、起飞重量取250 t的情况下，最优巡航条件应该在③过程中取到。结合图6的实验结果，最经济巡航高度应取10 400 m，约合34 000 ft；最经济巡航速度应取243 m/s，约合真空速472节，校正空速284节，巡航马赫数0.817 Ma。