基于DTCWT域统计特征融合的纹理图像检索

2020-07-05曲怀敬王恒斌徐佳王纪委魏亚南

山东建筑大学学报 2020年3期

曲怀敬，王恒斌，徐佳，王纪委，魏亚南

（山东建筑大学信息与电气工程学院，山东济南250101）

0 引言

随着多媒体数据库和计算机网络的广泛应用，其包含的海量有用视觉信息需要采用基于内容的图像检索CBIR（Content-Based Image Retrieval）技术进行自动、快速而准确地查访［1］。纹理是自然图像的一种便于区分的基本视觉特征，也是呈现在其中的一种基本形态［2］。纹理图像代表了一大类自然图像，而纹理图像检索在图像处理、模式识别、计算机视觉、遥感监测、公安刑侦和医学诊断等领域中得到了广泛的应用［1，3－4］。由于纹理图像可以视为一个随机过程的实现，因此目前基于统计建模的纹理图像检索已成为CBIR领域的前沿研究内容。

通常，优良的基于变换域统计建模的纹理图像检索系统需要较低复杂度的多尺度变换、有效的分布参数估计方法和只依赖于统计参数的相似性测度。近十几年来，围绕这个要求，众多学者提出了许多基于变换域统计建模的纹理图像检索方法。Do等［5］在离散小波变换域将纹理图像高频子带建模为广义高斯分布GGD（Generalized Gaussian Distribution）；Kwitt等［6］在双树复小波变换域将纹理图像高频子带幅值系数建模为Gamma分布或Weibull分布；Yang等［7］基于非下采样Contourlet变换将方向子带系数建模为Weibull分布；杨娟等［8］在双树复小波变换域将细节子带系数建模为双广义高斯分布；Vo等［9］将均匀离散Curvelet复变换域的实部和虚部子带建模为GGD分布、相对相位子带建模为Vonn分布；李朝荣等［10］在离散小波变换域，将细节子带系数建模为高斯Copula联合统计分布，在上述方法中，相似性测度均采用K-L（Kullback-Leibler）距离。

纹理可以视为由位置、尺度和方向上覆盖范围广泛的多重分量叠加而成。如上所述，大多数纹理图像表示的方法采用的是单一类特征，不能充分地反映局部纹理的细节结构，从而丢失了刻画纹理图像的许多重要信息。为此，需要采用多类特征互补融合的方法来解决这一问题。近年来，多特征融合与对应的相似性测度加权组合是广泛采用的、有效的纹理图像检索方法［11］，在多尺度变换域，将各子带系数的统计特征进行互补融合可以有效地提高纹理图像检索的性能。殷明等［12］基于非下采样剪切波变换域提出一种纹理图像检索方法，其中特征向量采用广义高斯分布参数特征和RI－LPQ特征融合，相似性测度采用K－L距离和欧氏距离的加权平均。Ves等［13］在小波框架域将纹理图像高频水平和垂直子带组合构成复值子带，并将其幅值系数建模为广义Gamma分布，相位系数建模为广义von Mises分布，相似性测度基于这两种分布参数特征融合选用最优加权的对称K－L距离。Qu等［14］在金字塔双树方向滤波器组复变换域，将高通子带系数建模为广义高斯分布，复值方向带通子带的幅值系数建模为Gamma分布并融合了相对相位的能量特征，相似性测度选用闭式K－L距离和欧氏距离的加权平均。这些方法大多利用了高频复值子带的幅值信息和相位信息，但并未对低频概貌子带的信息进行利用。

在基于金字塔双树方向滤波器组复变换域对纹理图像检索方面的探索研究工作中，提出了一种基于混合建模的纹理图像检索方法，将高频子带系数建模为广义高斯分布、幅值带通子带系数建模为Weibull分布，但是没有利用概貌子带和相位子带系数信息［14－15］。为充分利用复变换域各子带系数，特别是相位子带系数的统计特征，同时考虑到金字塔双树方向滤波器组复变换域存在相位子带信息刻画不足的问题，文章提出一种在双树复小波变换DTCWT（Dual-Tree Complex Wavelet Transform）域融合低频概貌子带和高频复值细节子带统计分布特征的纹理图像检索新方法。其中，低频子带采用变换系数的能量特征和归一化欧氏距离；高频幅值子带系数采用Weibull分布参数特征，而高频相对相位子带系数采用wrapped Cauchy分布参数特征，二者的相似性测度都采用K－L距离。将这些统计特征进行融合，并对相应的相似性测度进行最优加权平均求和。通过对VisTex纹理图像库进行检索实验，以验证新方法能否有效地提高检索性能。

1 双树复小波变换域中的统计特征提取

DTCWT根据树形结构，采用低通和高通滤波器组，分别同时进行实部和虚部的多尺度子带分解。最终在每尺度下，得到1个组合的低频概貌子带，以及6个不同方向（±15°、±45°、±75°）的高频复值子带。相应地，可得到每尺度下6个实部高频细节子带和6个虚部高频细节子带。

1.1 低频子带系数的能量特征提取

在一幅纹理图像中，纹理的分布与灰度值的变化息息相关。灰度值变化的程度越大，在纹理中体现的信息就越丰富，而这种变化在变换域中就体现在每个子带的能量分布上。因此，纹理图像的子带能量可以表征其纹理信息。

在双树复小波变换域分别提取纹理图像1～3层的概貌子带系数的分布能量作为特征。能量特征分别由式（1）和（2）［5］表示为

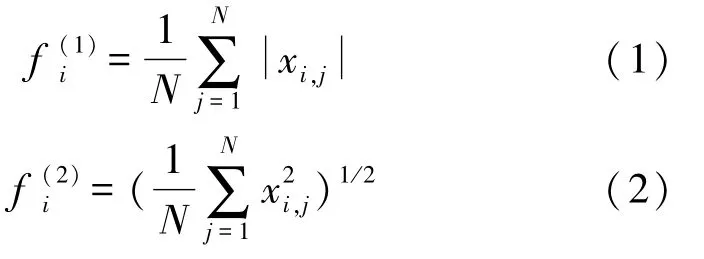
式中：N为概貌子带系数的总量；xi，j为第i层概貌子带的第j个变换系数。

1.2 幅值子带系数的统计特征提取

在DTCWT变换域，对于高频幅值子带系数，根据其直方图的包络形状，可选用Weibull分布模型进行描述。其概率密度函数p（x；β，λ）由式（3）［6］表示为

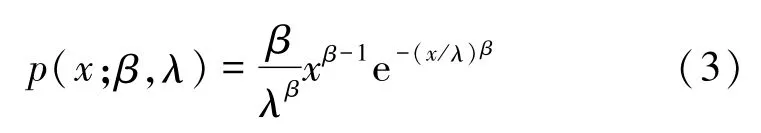
式中：x为幅值随机变量，0＜x＜∞；β为形状参数，β＞0；λ为尺度参数，λ＞0。

Weibull分布参数的估计通常采用最大似然的方法。给定 Weibull分布随机样本集X ＝{x1，x2，…，xΝ} ，并假定样本是独立同分布的，则定义似然函数L由式（4）表示为

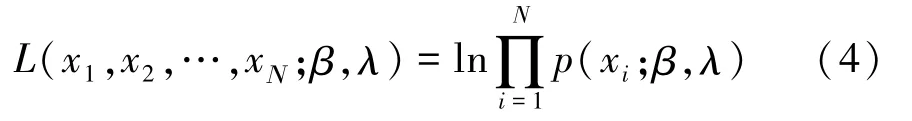
根据最大似然估计方法，则尺度参数λ与超越方程分别由式（5）和（6）表示为

式（6）可通过Newton-Raphson迭代方法进行数值求解［6，15］，求出形状参数β，则由式（5）可确定尺度参数λ。

只有当所选的初值和真实值相接近时，Newton-Raphson迭代方法估计的结果才准确。因此，采用变步长迭代算法估计形状参数β［15］，β的初值由方差系数根据查询表确定。方差系数KC由式（7）表示为

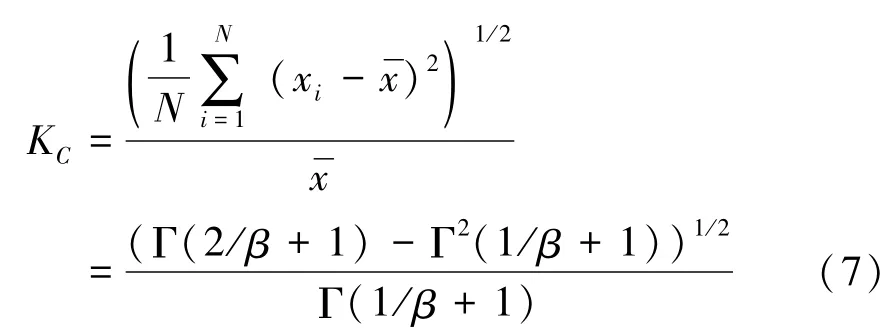
式中：为 Weibull随机分布样本集X ＝{x1，x2，…，xN} 的均值Γ为Gamma函数。

1.3 相对相位子带系数的统计特征提取

纹理图像经过双树复小波变换后，由各尺度下的复值子带系数可以得到对应的相位子带系数。通常，相位子带系数直方图的分布是均匀的［16］，如图1所示。然而，这种均匀分布的相位不能产生区分纹理图像的任何信息，为此需要采用相对相位。在相位子带的空间位置（i，j）处，定义相对相位θ（i，j）由式（8）表示为

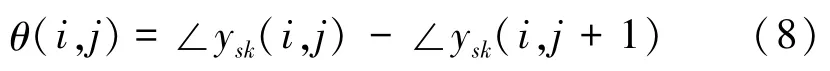
式中：∠为相位；ysk（i，j）为在s尺度、k方向子带下，位置为（i，j）处的复值系数。

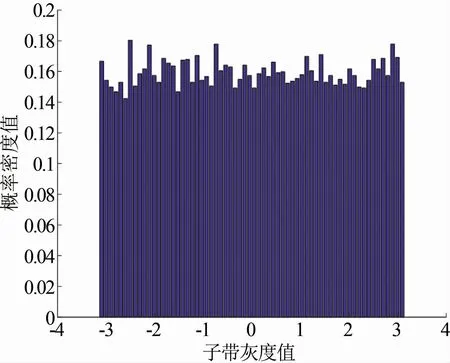
图1 相位子带系数分布直方图

相对相位子带系数分布直方图如图2所示。相对相位系数的统计分布可以有效地刻画纹理图像的区分信息。通常，相对相位系数可通过wrapped Cauchy分布进行有效地建模。wrapped Cauchy分布的概率密度函数p（θ；ρ，μ）由式（9）［16］表示为

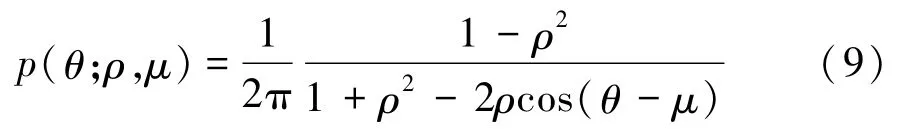
式中：θ为相对相位系数，θ∈［－π，π］；μ为位置参数，μ∈［－π，π］；ρ为尺度参数，ρ∈［0，1］，其值越大，对应的概率密度曲线就越尖锐。

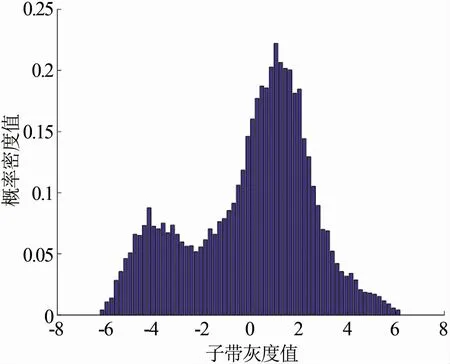
图2 相对相位子带系数分布直方图

给定一组独立的、符合wrapped Cauchy概率密度p（θ；ρ，μ）分布的观测数据集合｛θ1，θ2，···，θN｝，根据最大似然方法，采用迭代算法可估计位置参数和尺度参数［16］。其中，迭代方程分别由式（10）～（12）表示为

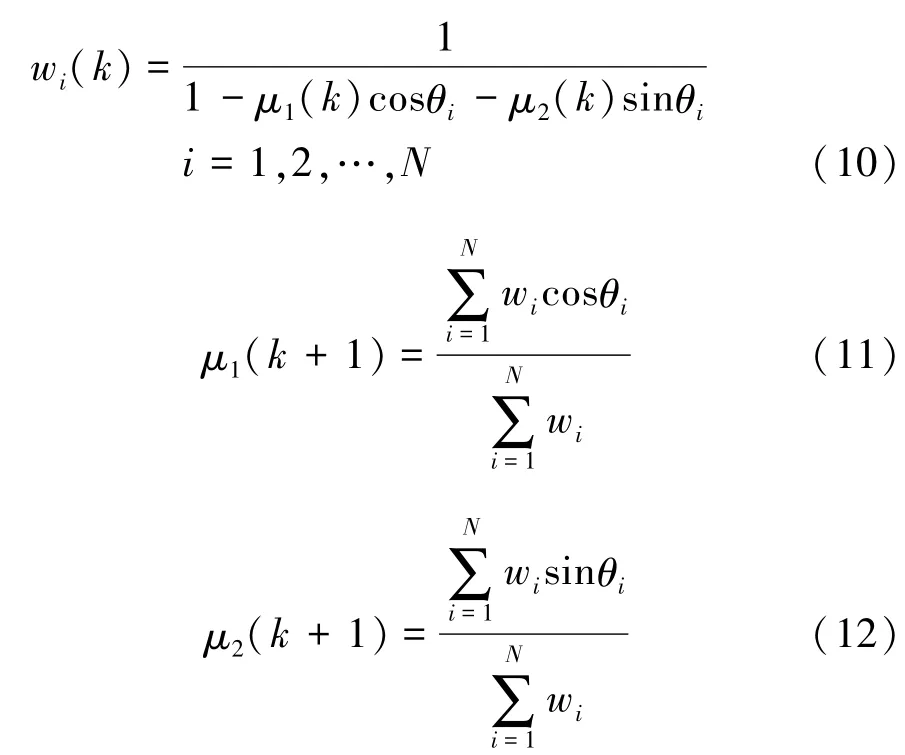
式中：k为迭代指针。

当迭代算法收敛后，分别得到估计值μ1和μ2，则位置参数μ和尺度参数ρ的估计值分别由式（13）和（14）表示为

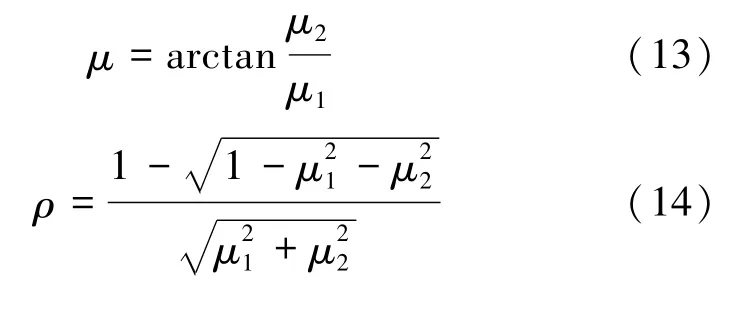
2 基于统计特征融合的纹理图像检索方法

2.1 纹理数据库的建立

为了便于检索性能的比较，所采用的实验图像取自广泛使用的VisTex数据库［5］，包括40类大小为512 pixel×512 pixel的彩色纹理图像。纹理数据库建立步骤为：（1）将彩色纹理图像变换为灰度图像；（2）将每一个图像不重叠地分割为16个128 pixel×128 pixel的灰度子图像。最终建立了一个具有40类、每类16个子图像、总数为640个的灰度纹理图像标准实验数据库。为了减少同类子图像间灰度值的相关性和保持检索过程的公平性，将所有子类图像分别归一化为零均值和单位标准差。

式中：p（x；β1，λ1）和q（x；β2，λ2）为数据库备选图像和查询图像的Weibull概率密度函数；γ为欧拉常数。

对应于相对相位特征，由于wrapped Cauchy分布不存在一个闭式形式的K－L距离，因此相似性测度Dph可根据K－L距离定义，通过数值分析的方法

2.2 检索过程与评价

检索过程是在未标记的纹理图像库中搜索和某一个查询图像最相似的若干同类图像。通常，采用平均检索率来定量评价检索系统的性能。在典型的检索实验中，查询图像选为数量为Nt的纹理图像库中的任一图像。对于每个查询图像，检索得到的所有正确图像是同类的其他Nr个图像。而对于第i个查询图像，假定在检索得到的前M个最相似图像（不包括查询图像本身）中所包含同类图像的个数为ni（M），则平均检索率Ra由式（15）表示为

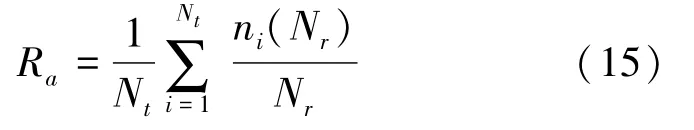
在纹理图像检索实验中，数据库图像的个数Nt为640，而与每个查询图像同类的其他备选图像的个数Nr为15。

2.3 纹理图像统计特征的计算

获取纹理图像统计特征的步骤是：（1）计算纹理图像经双树复小波分解后产生的低频子带的能量，并作为能量特征；（2）对小波分解后得到的高频子带幅值系数进行Weibull建模，模型的两个分布参数作为幅值特征；（3）将高频子带相对相位系数建模为wrapped Cauchy分布，模型的两个分布参数作为相位特征。对于每一分解层，能量特征数为1×2＝2，幅值特征数为1×6×2＝12，相位特征数为1×6×2＝12。

2.4 相似性测度的计算

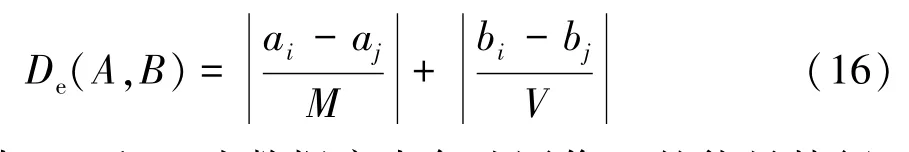
对应于能量特征，选用归一化欧式距离De作为相似性测度，其定义由式（16）表示为式中：ai和bi为数据库中备选图像A的能量特征；aj和bj为查询图像B的能量特征；M和V分别为整个数据库的能量特征

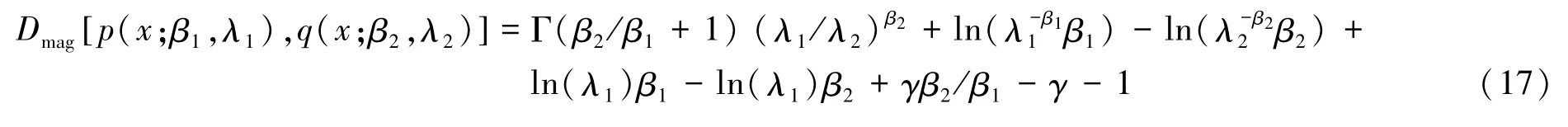
估算，由式（18）表示为

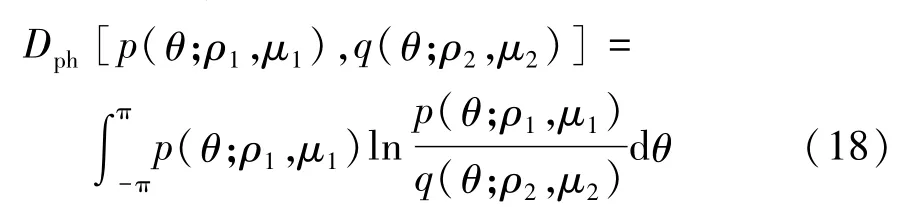
式中：p（θ；ρ1，μ1）和q（θ；ρ2，μ2）分别为数据库备选图像和查询图像的wrapped Cauchy概率密度函数。

采用的总相似性测度D由式（19）表示为

式中：a＋b＋c＝1，且a、b、c的取值范围为［0，1］。

利用提出的检索方法，通过Matlab仿真，遍历整个a和b的取值范围，取值步长为0.05；并根据最优平均检索率，选择a＝0.25、b＝0.35和c＝0.4。

3 纹理图像检索实验结果与分析

3.1 幅值子带系数的统计模型选择

随机选用VisTex数据库［5］中的Fabric.0009和Food.0005作为典型的实验图像，如图3所示，对其进行3层DTCWT变换。为了比较，针对第1层的－15°高频复值子带的幅值系数分别进行Weibull分布、Gamma分布［6］和GGD分布［5］建模以及相应的直方图拟合。Fabric.0009、Food.0005图像的实验结果分别如图4（a）～（c）、（d）～（f）所示，各分布图下括号里的数值分别为尺度参数、形状参数和熵差率。其中，熵差率（ΔH／H）是用来衡量概率分布拟合程度的客观参数，其定义为直方图和模型分布之间的K－L距离或相对熵（ΔH）与直方图分布的熵值（H）的比值，其值越小说明拟合得越好。

图3 VisTex数据库中的典型实验图像

由图4可知，对于高频复值子带的幅值系数，根据熵差率的数据，采用Weibull和Gamma分布进行统计建模比较准确，而采用GGD分布建模不太合理；相比较而言，Weibull分布建模由于初值选择合理，收敛性较好，其拟合的熵差率最小，拟合效果最好。因此，选用Weibull分布模型的两个参数作为幅值子带的特征。

由图4（a）和（d）的数据比较可知，两个不同类纹理图像的Weibull分布参数之间有着明显的数值差异，因此特征间具有明显的区分能力。可以预期，由于分布参数特征提取的准确性较高、区分性较好，从而能够保证检索系统的性能得到有效的改善。

3.2 相对相位子带系数的统计模型选择

同样地，为了比较，随机选用VisTex数据库［5］中的Fabric.0007和Fabric.0009作为典型的实验图像，如图5所示，并对其进行3层DTCWT变换。针对第1层的－75°高频复值子带的相对相位系数分别进行von Mises分布、wrapped Cauchy分布和Vonn分布建模［9，16］和直方图拟合。Fabric.0007、Fabric.0009图像的实验结果分别如图6（a）～（c）、（d）～（f）所示，各分布图下括号里的数值分别为位置参数、尺度参数和熵差率。

由图6可知，对于高频复值子带的相对相位系数，根据直方图拟合的效果及熵差率的大小，3种分布模型的拟合效果差别并不太大，相比较而言，wrapped Cauchy分布的建模准确性较高。并且，与VisTex数据库所有图像拟合的平均效果相比，wrapped Cauchy分布的模型拟合效果要优于其他两个模型分布。因此，选择wrapped Cauchy分布对相对相位系数进行建模，并以此分布参数作为相对相位子带的特征。

由图6（b）和（e）的数据比较还可知，两个比较接近的不同类纹理图像的wrapped Cauchy分布参数之间也有着明显的数值差异，特征间的区分能力较好，从而有助于提高检索系统的性能。

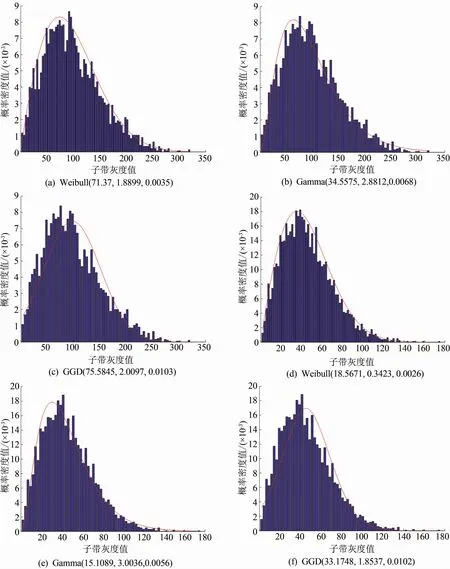
图4 幅值子带系数的统计建模图

图5 VisTex数据库中的典型实验图像

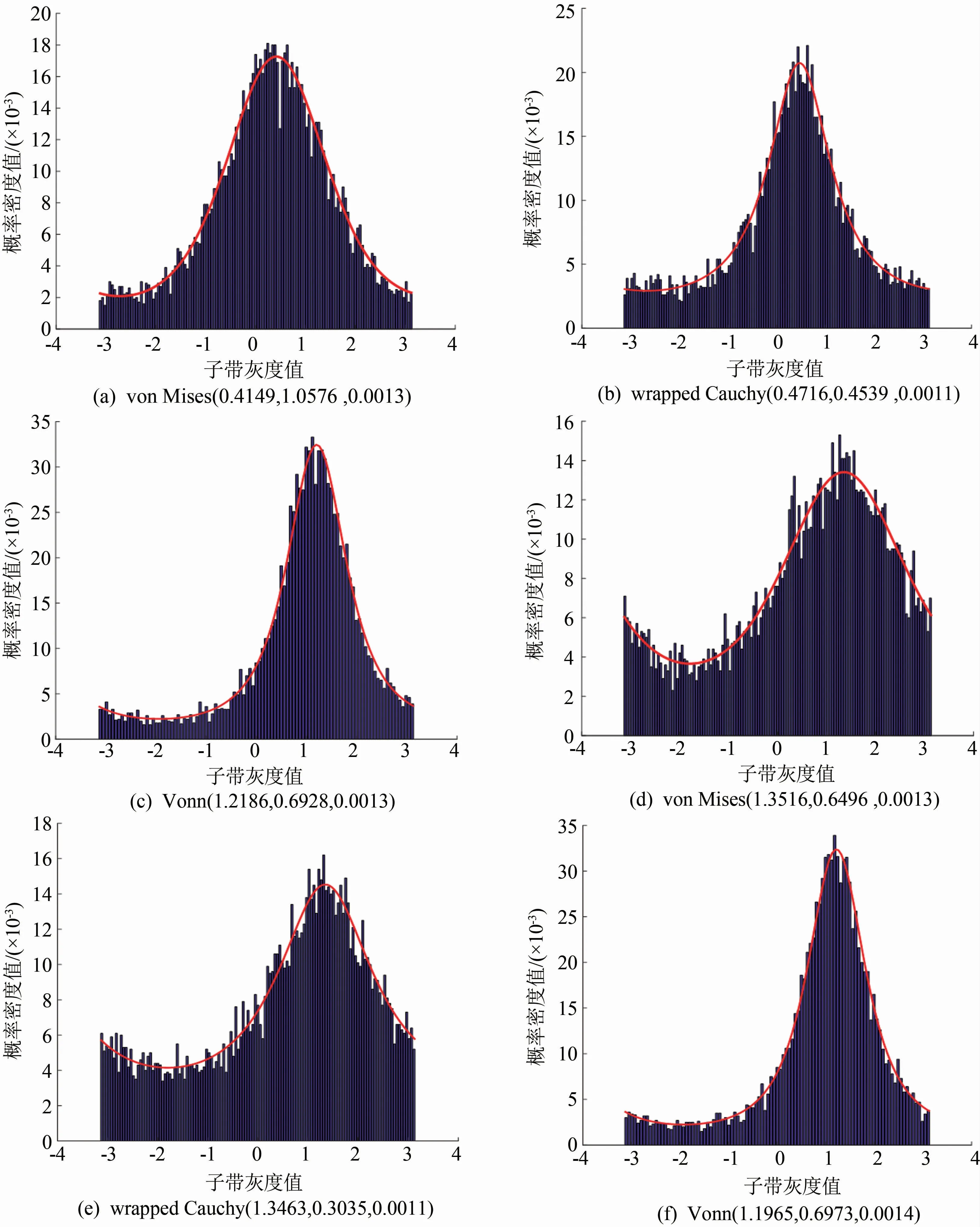
图6 相对相位子带系数的统计建模图

3.3 分解层数的选择

对于用于图像统计建模的多尺度变换，分解层数的选择应保证最小子带图像尺寸≥16 pixel×16 pixel。否则，对所估计的子带能量值及模型参数值的准确性都会产生不良的影响。由于实验中选择的是VisTex纹理图像库，所采用的每类子图像大小为128 pixel×128 pixel，因此选择的最大分解层数为3层。能量特征和幅值子带统计特征都是根据DTCWT分解成3层而提取的。

对于相对相位子带特征的提取，所需的最佳分解层数并没有具体的依据。为此，仅针对相对相位特征，分别进行了DTCWT的1～3层分解的纹理图像检索实验，平均检索率依次为72.01%、77.42%、73.96%。因此，从最佳检索性能角度出发，相对相位特征提取采用的分解层数为2层。

综上分析，最终采用的实验方案为：对于能量特征，选择3层DTCWT分解，每层取1个概貌子带，特征数为3×1×2＝6；对于幅值特征，选择3层DTCWT分解，每层取6个幅值子带，特征数为3×6×2＝36；对于相对相位特征，选择3层DTCWT分解的前2层，每层取6个相对相位子带，特征数为2×6×2＝24。最后，实验所取的总特征数为66。

3.4 不同方法的检索性能比较

根据提出的检索方法，以平均检索率为性能指标，通过与其他典型检索方法的最好结果进行性能比较说明其有效性。选用这些方法进行比较的原因，是因为其采用了与文章相同的纹理图像数据库以及检索性能评价指标，并且多尺度变换均采用3层分解。其中，L1＋L2方法采用的特征是实小波子带的均值和方差，相似性测度采用归一化欧氏距离［5］。GGD方法采用的特征是实小波变换域细节子带系数的GGD分布参数，相似性测度采用K－L距离［5］。GGD－WC方法的特征采用均匀离散Curvelet复变换实部和虚部子带的GGD分布参数、相对相位子带的wrapped Cauchy分布参数，相似性测度采用K-L距离［16］。GGD-Vonn方法的特征采用均匀离散Curvelet复变换实部和虚部子带的GGD分布参数、相对相位子带的Vonn分布参数，相似性测度采用K-L距离［9］。Copula方法的特征采用Copula联合统计建模的分布参数，相似性测度采用K－L距离［10］。Ves方法的特征采用小波框架变换域细节子带的广义Gamma分布参数和相位的广义von Mises分布参数，相似性测度采用加权的对称K－L距离［13］。Yang方法的特征采用无下采样Contourlet变换域方向子带的Weibull分布参数，相似性测度采用K－L距离［7］。

采用上述方法得到的平均检索率依次为64.83%、75.73%、85.64%、85.82%、83.58%、80.78%了86.74%，具有更好的检索性能。由于在DTCWT多尺度多方向复变换域，文章方法对图像的所有子带统计信息都进行了充分的利用，并通过多特征互补融合有效地刻画了纹理图像的方向分布特征。同时，最优地利用了相似性测度的加权组合，从而有效地改善了纹理图像检索系统的性能。