Scrateh递归程序设计的教学探讨

江玉珍 朱映辉 邓清华 王晓辉 陆锡聪

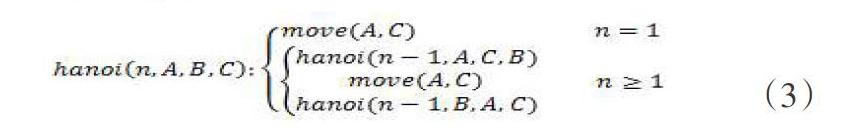
摘要：在常规的程序设计教学中，递归算法能在运行过程中实现自我调用，能将大问题层层转化为小规模相似问题来进行求解，虽然其理解上抽象难懂但却能够轻巧地解决很多复杂问题，是结构化程序教学上重点和难点。通过对递归算法原理的分析，提出抓住三个要点及构造递归表达式的学习方法。结合Scratch简洁的编程风格，通过举例提出基于Scratch的递归算法教学引导思路，并分析探讨更有效的递归教学方法。

关键词：递归;回溯;递推;Scratch;汉诺塔

中图分类号：G642 文献标识码：A

文章编号：1009-3044（2020）15-0158-02

1引言

在计算机各种语言的程序设计教学上，学生掌握了循环和函数应用后，就会接触到递归算法程序设计。递归算法是程序教学中的一个难点，因为它太抽象，不像循环那样具体，学生往往会因难以深入地跟踪到函数自我调用中各层次间参数的传递关系，而对它产生抗拒的情绪。然而，递归算法又是程序教学中的一个不能规避的重点，因为它是一种优雅的问题解决方法，许多多重循环难以实现的问题，用递归算法却总能轻巧地迎刃而解。虽然所有的递归算法最终都可以使用非递归方法来实现，而且当同一问题同时用循环和递归解决时，递归算法通常没有性能上的优势，因为它在自我调用时必须使用堆栈来辅助处理。但是，当一些复杂问题面临解决时，使用递归算法却总能在第一时间获得解决方法，而且程序简洁直观，这正是它无可比拟的优势，也是它作为编程教学重点的原因。

2递归算法的编程要点

递归函数的调用过程又分成两个部分，回溯阶段和递推阶段。前半部分是回溯阶段，就是把大问题层层轉化为较小的问题，每次递归调用都会简化原始问题，让它不断地接近最简状态，这样一旦达到最简状态时就结束递归调用，进入递推阶段，将小问题求解结果又层层转换为大问题求解结果，直到初始问题获解。因此，在递归算法设计中，有以下三个要点：（1）要有明确的递归终止条件，防止程序陷入无限调用;（2）要有明显的判断语句来引导递归调用走向;（3）过程或函数自身的调用要趋向递归的终止条件。

对此，在教学上，可以引导学生先对复杂问题进行剖析、写成递归表达式，递归表达式必须具备上述三个要点，然后再进行程序编写，这样可以起到事半功倍的作用。比如，对于n！的递归函数，可以写成式（1）表达式。

该两个表达式中，第1行表示递归终止条件，即问题的最简状态。第2行表示递归自我调用的关系，用于表示“n问题”至“n-1或n-2问题”的转换关系，并反映出调用趋势是向着递归终止条件发展的。

3Scrateh的算法程序设计

Scratch是麻省理工学院（MIT）设计开发的一款面向编程初学者的图形化编程工具，其功能丰富易学易用，有助于学生逻辑计算思维的锻炼嘲。对于程序初学者尤其青少年而言，学习编程其实并不是为了会写代码，而是为了将想法变成现实，实现一个完整的问题解决方法。Scratch就提供这样一个便利的平台，它可以不用花太多精力去关注那些易出错的语法表达和数据结构，让开发者更专注于解决方法的运用。Scratch自推出至今已经历多次改版升级，Scratch3.0具备自定义模块（过程）功能，既适合常规图形互动类程序设计，也非常适合算法类的程序设计。而且，Scratch与其他程序语言一样，能够支持带参的自定义模块的自我调用，所以利用Scratch可以更容易地实现递归算法。

根据自调用模块的返值情况，递归算法可分为递归过程（没有返值）和递归函数（有返值）。Scratch3.0自定义模块本身可以带参，但不能返值，因此在递归过程和递归函数的处理方法上略有不同，以下分别通过2个经典递归案例来分析说明各自实现方法的要点。

3.1递归过程的实现——Hanoi（汉诺塔）问题

汉诺塔是经典的递归算法问题，该问题若用非递归方法进行求解会非常烦琐，但使用递归方法求解却简单明了。设ha-noi（n，A，B，c）表示有n个盘子要从A座借助B座移动至c座，move（A，C）表示将最上面一个盘子从x座移动至Y座，则该问题的递归表达式如式f3）。

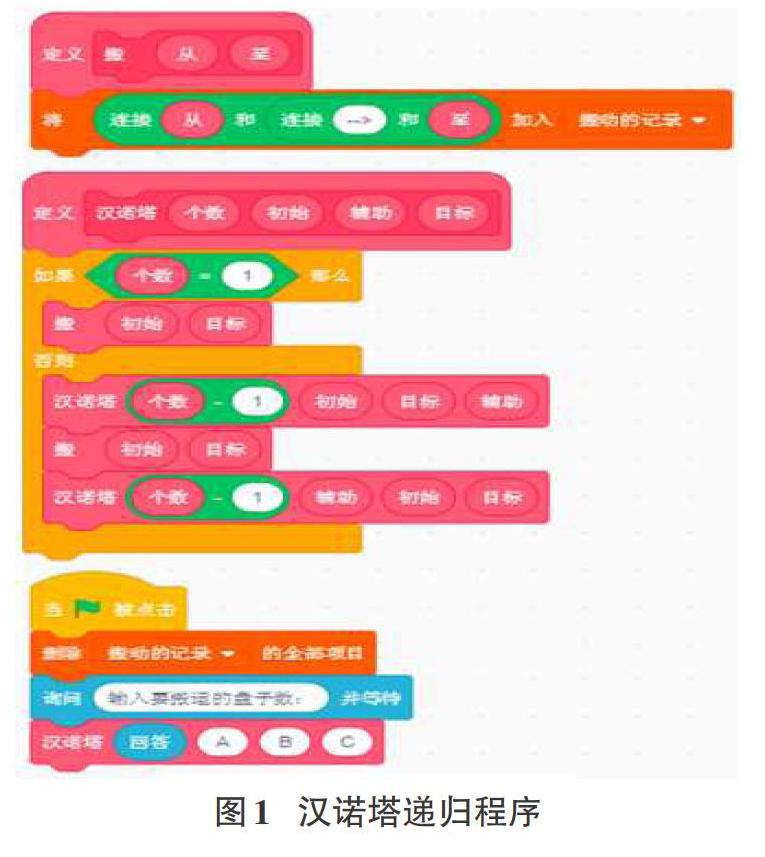
Hanoi（汉诺塔）n盘子问题的Scratch递归程序如图l所示。由图可见，该程序定义了2个模块：“汉诺塔”和“搬”分别对应式（3）中的“hainoi（）”和“move（）”，其中“汉诺塔”除调用“搬”模块外，还调用了2次自身，即“汉诺塔”，注意此时参数上的变动。借助列表对每次搬动状态的记录，程序运行后，用户输入初始盘子个数，列表将显示需搬动的总次数和搬动序列。

3.2递归函数的实现——卖鸭子问题

递归算法更普遍的用法是递归函数。如n！、Fibonacci数列等在表达成递归函数时均有一个函数返回值，这个返回值在递推阶段也起到重要的向上层传值的作用。既然Scratch自定义模块不能像普通函数那样获得返回值，那么又该如何实现带返值的递归函数呢？对于这个问题，解决的办法其实并不难，只需增设一个外部变量来代替函数值，在模块递归调用后对该变量进行迭代赋值即可。

卖鸭子问题：农夫赶着鸭子去每个村庄卖，每经过一个村子卖去所赶鸭子的一半又一只。这样他经过了m个村子后还剩n只鸭子，问他出发时共有多少只鸭子？若用ducks（x）表示经过m个村子前鸭子的总数，那么该问题的递归表达式如式（4）。

Scratch程序实现时，自定义递归模块方法和主调程序如图2所示。由图2可知，“算鸭子”是自定义的递归模块，即其内部又调用了“算鸭子”。为传递内外递归模块的返回值，“算鸭子”模块内部使用了一个外部变量“原有鸭子总数”，每次递归调用后该变量值均做迭代更新，所以该变量实际上就起到函数返回值的作用。

4结论

递归算法虽然运行效率不高，但它的程序设计效率高且程序结构简洁清晰，教学上，重点是引导学生理解递归的实质是“分而治之”，即“大问题分解为本质相同的小问题”的思想。实际上在递归算法设计中，只要能找出问题内在的自我递推关系，紧紧抓住“递归终止条件”“判断引导”和“有趋向的自我调用”这三个要点、构建出其递归表达式，就能轻巧地将问题转化为递归功能模块并实现程序调用。在递归算法的掌握上，解决思路理解和运用远比程序编码更为重要，以c++为代表大多数的程序语言都能支持递归表示，但这些程序语言在编写递归程序时往往还要考虑大量语法表示、数据类型、数据结构等多种因素，程序也容易出现算法以外的错误从而加大编程者的调试负担。Scratch简单的程序设计方法一定程度上屏蔽了编程中在语法、数据结构等方面的诸多限制，让编程者更专注于算法设计本身，并在算法基础上实现程序的快速构建。因此，在算法程序教学上，它可以成为认知、理解及应用递归算法的一个良好的引导平台。