基于强化学习的海克斯棋博弈算法研究与实现

张芃芃 孟坤 杨震栋

摘要：本文旨在研究如何将强化学习模型合理地应用在海克斯棋博弈算法中，并给出程序实现方案。以蒙特卡洛树搜索生成数据集训练卷积神经网络的方式，使得模型能够在不断自我对弈的过程中，修正自身选择动作的策略，更新模型参数，从而达到提升棋力的目的。实验结果表明，通过强化学习算法能够准确地评估海克斯棋的局面，并有效地选择有利的落子位置，使得海克斯棋博弈系统获得高质量的决策能力。

关键词： 强化学习; 蒙特卡洛树搜索; 海克斯棋; 计算机博弈

【Abstract】 The purpose of this paper is to study how to apply reinforcement learning model to the algorithm of Hex game reasonably， and give the program implementation scheme. In this way， the convolution neural network can be trained by using the data set generated by the Monte Carlo tree search， so that the model can enhance chess skills by modifying the strategy of its own choice of action and updating the model parameters in the process of continuous self playing. The experimental results show that the reinforcement learning algorithm can accurately evaluate the situation of Hex game， and effectively select a favorable moves， so that Hex game system gains high-quality decision-making ability.

【Key words】  reinforcement learning; Monte-Carlo tree search; Hex game; computer game

0 引 言

随着人工智能的兴起，人们对计算机博弈的研究日趋深入，计算机博弈算法也已越来越多地被应用在各棋种上。海克斯棋是近年来比较流行的计算机博弈棋种之一，现已成为中国大学生计算机博弈大赛的竞技项目[1]。其规则很简单：博弈的双方依次在菱形的棋盘上落子，当任意一方最先将自己的两条边界用己方的棋子连接起来，则该方获胜。

强化学习也称增强学习[2]，是一类在自身智能体不断摸索和尝试的过程中，依靠环境带来的反馈更新自身决策方式的机器学习算法。当智能体模型做出某种动作后产生了有利的状态，则对模型进行奖励，反之则进行惩罚。以此不断迭代，最终使模型具有高质量的决策能力。本文将强化学习模型合理地应用在海克斯棋博弈算法中，使得模型能够通过不断自我对弈，提升棋力。

1 强化学习模型算法设计

海克斯棋是一种完全信息博弈，能够通过模拟大量對局来学习优良的落子选择方法。受AlphaGo Fan[3]和AlphaGo Zero[4]的算法启发，在模型的核心部分使用价值-策略网络二合一的卷积神经网络，使其输入原始棋盘，输出该局面输赢概率作为价值评估，同时输出每个落子位置获胜的概率分布作为策略评估。首先采取随机落子的方式，使用蒙特卡洛树搜索[5]生成大量对局样本，用监督学习的方式，根据最后的胜负结果、棋面状态以及走法的模拟来训练神经网络。以局面最终输赢训练价值网络的同时，用局面每个落子位置获胜频率分布训练策略网络。然后将这个模型加入到新建立的对手池中，并在从对手池中随机选择一个模型和最新模型进行对弈的过程中，同样通过蒙特卡洛树搜索模拟生成对局，从而产生对弈数据，对神经网络进行训练。并在将训练完成的模型加入到对手池中后，再利用新的模型继续模拟对弈，继而持续进行从对手池中选择模型对弈的过程，以此迭代出一个效果最佳的模型。

1.1 神经网络的设计

使用神经网络的目的在于能够对于给定的海克斯棋局面做出准确估价的同时，给出最佳的落子位置。因此选择多输出的卷积神经网络，使其同时具有价值输出和策略输出。

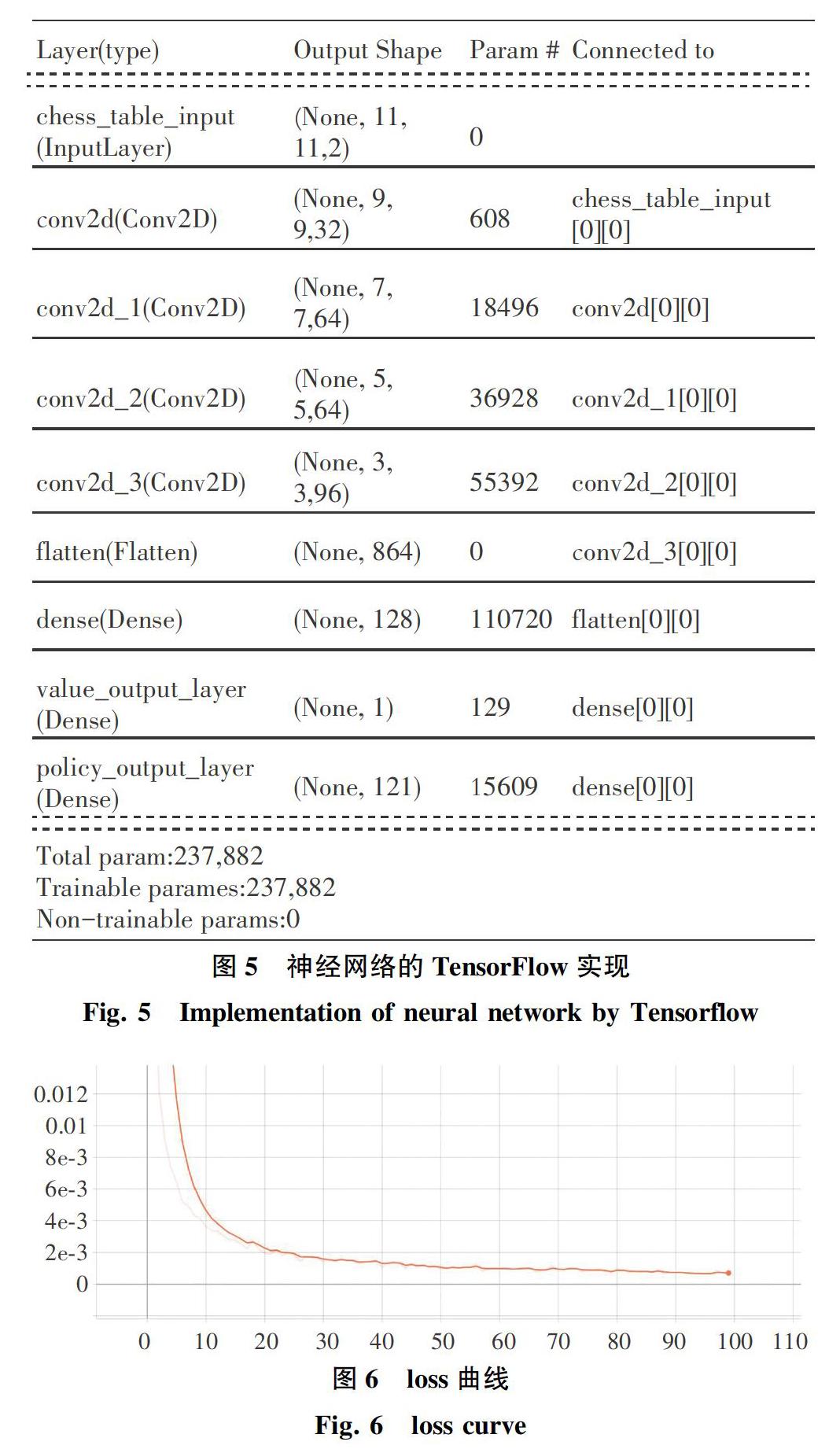
对于一个大小为11×11的海克斯棋局面来讲可以抽象成一个11×11×2的三维张量，作为模型的输入。其中，最低的维度用来区分棋盘上每一个位置的落子情况。考虑到3×3大小的卷积核刚好能够覆盖到任何一个方向上的双桥[6]，使得神经网络能够描述和考虑对局面影响较大的特定布局模式。因此在样本输入网络后，首先通过一个含有32个3×3卷积核的卷积层，再依次通过2个含有64个3×3卷积核的卷积层，然后通过一个含有96个3×3卷积核的卷积层，接着通过含有128个神经元的全连接层，最后通过一个神经元输出价值评估，通过一个含有121个神经元的全连接层输出策略评估。另外，所有的卷积层均使用线性整流函数作为激活函数，以保证在训练过程中误差反向传播的高效进行。神经网络结构图如图1所示。

1.4 自我对弈的训练过程

模型决策效果的提升主要依赖于自我对弈生成数据集来训练网络的过程，这需要维护一个对手池，用来存放模型的历代版本。由于不同模型仅在网络参数上存在区别，因此在对手池中存放模型等价于存放网络参数。故首先将监督学习训练完成的网络参数放入对手池中，每次从中随机选取一个网络参数组成模型后作为最新加入对手池的网络参数所组成模型的对手，进行多次双循环对弈，将对弈过程中的局面用其胜负结果标注其价值，并使用蒙特卡洛树搜索获得其策略标签。再用新生成的数据集训练当前的网络，以此获得新一代的网络参数，并放入对手池中，继续自我对弈。模型自我对弈过程的数据流图如图3所示。