启发式教学与立体几何教学的结合

苏孟琪

摘 要：以《直线与平面所成角》为例，通过探究实验、信息技术手段、设置问题串作为线索等手段启发学生，渗透类比、降维等思想，提高学生的逻辑推理能力。同时也存在线面角的引入缺乏直观性、唯一性的讨论过早等问题，从考试数据来看，学生找角的能力也较弱。

关键词：启发式教学;直线与平面所成角;信息技术

一、教学背景

（一）学生情况

在前面的学习中，学生已经掌握了空间中点、直线、平面之间的关系，学习了直线与平面平行的定义、判定定理以及性质定理，初步运用过“降维”的思想方法来处理一些问题。在这个过程中，学生的几何直观得到了进一步的发展，逐渐开始建立空间观念。与此同时，学生本身的几何知识水平仍然停留在平面几何阶段，并且立体几何的图形和人们日常生活的图形结构存在一定的差异性，这使得学生更加不好理解立体几何。另一方面，学生正处于从形象思维到抽象思维的转折阶段，逻辑思维能力不足，很难理解立体几何知识点间的逻辑关系，只能通过死记硬背的方式去记忆，在解题的过程中，学生只能将公式定理当做模板去套用，没有灵活性。因此，如何启发学生主动探索是立体几何教学的重点。

（二）教学情况

在学习立体几何之前，学生进行了必修五《解三角形》和《数列》的学习，明显表现出对《数列》学习的不适应性，一是不能抓住数列明显的结构特征来联系知识点解题;二是不能顺畅地进行逻辑推理，涉及到多层推理的问题很多学生都选择放弃;三是知识点间的联系非常薄弱。这些问题到立体几何部分更加严重，学生只能处理直接明了的证明题。

在立体几何的证明中，学生的书写非常混乱，辅助线的构建也很杂乱，这也从侧面反映出学生在证明过程中的逻辑是比较混乱的。在平常的教学中，教师一般都是画图+实物演示结合进行教学，学生往往听得似是而非，对定义定理的理解模棱两可，没有建立起一个具体的几何模型。图像与实物间也需要一条桥梁，帮助学生将平面图像转化成空间中的立体图形，信息技术是最好的方式。

二、教学设计的特点

为了缓解或者解决上述问题，我的教学设计采用了启发式教学，以“降维思想”为核心，首先通过复习让学生回忆“降维”在立体几何中的应用，然后围绕选平面中的哪条线与斜线所成角来替代线面角展开，设计实验先让学生提出假设，随后通过GeoGebra演示平面中不同的直线与斜线所成角的规律，然后得到结论。最后再利用数学符号语言对结论给予严格的证明。

这样的研究符合知识发展和学生的认知规律，在这个过程中，学生既从直观上理解了斜线与其射影在平面上所成角的优越性，也从逻辑上给出了严格证明，既有数也有形，多个方面帮助学生理解线面角的定义。

三、教学设计的优点与不足

（一）教学设计的优点

1. 以“降维”为核心设计问题串

学生对直线与平面所成角只有一个感性的认识，如何将这个感性的认识一步步剖析开，用理性思维去认识是设置问题串所需要解决的问题。

部分教学设计

教学环节 教学过程 设计意图

【任务一：复习旧知】

【任务二：探究定义】

步骤一：

问题1：平面内的直线与斜线的位置关系是怎样的？

问题2：用平面内哪条过斜足的直线与斜线所成角来刻画直线与平面所成角？

情况一：用斜线在平面上的射影与斜线所成角来替代直线与平面所成角

情况二：不清楚应该用哪条

教师引导：我们回忆一下距离的定义，两点间的距离和点到直线的距离我们都用的是最小距离来定义，用最小量定义是我们常见的定义方式，因此我们有了定义的方向，利用最小的线线角来定义线面角

步骤二：实验探究

1. 提出问题：平面内哪条过斜足的直线与斜线所成角为最小角

2. 提出假设：斜线在平面内的射影与斜线所成角为最小角

3. 实验探究：利用GeoGebra演示平面中不同的直线与斜线所成角

4. 实验结论：

首先任务一通过复习引导学生回忆“降维”的思想方法，以它作为定义线面角的切入点，帮助学生找到研究的方向。

紧接着任务二中，第一个步骤利用问题1解决了与斜线异面的问题，进一步缩小了平面中的直线范围，通过问题2和教师的引导帮助学生进一步确定选取直线的标准，同时提升学生类比的能力。第二个步骤的实验探究在学生已经有了猜测的基础上，通过信息技术将规律直观展示给学生，帮助学生建立对定义的直观感知。

在这样的问题设计中，教师更多地扮演着引导者和启发者的角色。教师通过关键的问题启发学生让学生自主思考，让学生深入到定义里，从多个角度去研究去理解而不是浮于表面。

2. 使用信息技术，增添了直观感知性

直线与平面所成角的定义中，为什么选择斜线的射影是研究定義的核心，也是学生难以理解的地方，很多教师在处理时选择先给定义，再严格证明解释原因。在这个过程中，学生并没有获得直观的图形信息，因此严格的证明也没有起到加强解释的作用，对于学生而言更多的是增添了负担。

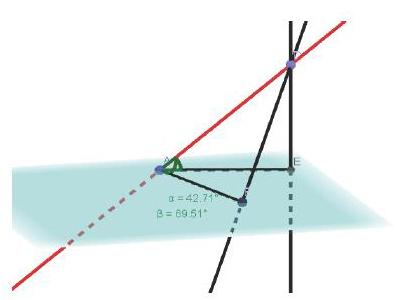
基于这样的情况，设置了一个实验探究，教师利用GeoGebra软件动态演示，选取不同的平面内直线，测量此时所成的线线角，再拖动直线的位置直观呈现角度的变化。通过这样的过程，学生能够建立一个具体的模型，对定义也有了直观的理解。

3. 例题设置较好，帮助学生多角度理解射影

当学生利用定义去求线面角时，找不到射影是学生最严重的问题。通过连接斜足和垂足来确定射影，因此问题就转化为如何确定平面的垂线。

例1：如图所示，正方体中，求：

（1）与面所成角的正弦值;

（2）与面所成角的正弦值;

（3）与面所成角的正弦值;

例2：如图，在四棱锥中，底面是正方形，侧棱底面，，是的中点，求与底面所成角的正切值。

两个例题由浅入深，从学生最熟悉的正方体模型开始，让学生感受并寻找正方体中的垂直位置关系，同时也让学生意识到每个方向都有射影，找射影先找平面垂线。当学生逐渐熟悉找线面角的步骤后，再以棱锥为模型，并且已经给了平面的垂线，降低了习题的难度。

在习题设置上，先让学生在熟悉的模型里面操作，熟悉的模型未知的内容少，难度低，学生能将注意力更多地集中于找线面角上。然后更换模型，稍微提高难度考察学生。在这样阶梯式的过渡中，学生能够更好地掌握方法。

（二）教学设计的缺点

1. 教学中对找角的训练不足

在本次期末考中，立体几何内容共考了四题，其中有两题与找角有关，年级得分情况如下表。

这两道题属于综合性题目，找角是解决这两个题目的关键。从上表数据以及考后反馈来看，学生要么是看到题目与找角有关就跳过，要么就是找不到角或者找到的角是错误的。

线面角是异面直线所成角研究的继续，也是研究二面角的基础。它在异面直线所成角的基础上结合了平行和垂直的位置关系，更加考察学生的空间想象和逻辑推理能力。因此这节课的主要内容是线面角定义的生成，而难点是如何寻找线面角，但是如何寻找线面角只在习题中体现出来，学生的训练不到位。

2. “最小角”的证明可能过早

学生观察出斜线在平面上的射影与斜线所成角为最小角是很容易的，当有了这样一个认知以后，线面角的定义也就呼之欲出了，严格地进行证明不是必须的，对于水平不同的班级，是否需要严格证明要视学生情况而定。

3. 射影强调不到位

射影是线面角的基础，但是这份教学设计对射影只是匆匆略过，强调不到位影响后续练习效果。如图所示，斜线与其在平面上的射影可以构成，因此可以利用直角三角形求线面角的正余弦值和正切值，计算量就小了很多。这个直角三角形要多加强调，让学生加深印象。

四、教学设计的改进方案

针对上述问题，提出以下改进方案。

通过演示光从上往下照射，斜线在平面上留下影子，借此引出射影的概念，随后教师进行板书，在黑板上演示一遍射影的画法，最后强调此时形成了一个直角三角形。通过一系列的设问探究后得到线面角的定义，此时教师需要一边复述定义，一边画出线面角，再次强调此时通过射影的定义形成了一个直角三角形，这能够降低我们的计算量和计算难度。

找角作为学生的一大难点，一方面与学生的线面垂直的判定功力有关，另一方面也与不熟练找角的程序性操作有关。因此建议在给出线面角的定义后，给出学生找线面角的程序性步骤：第一步过直线上一点做平面垂线交平面于点，第二步连接斜足和垂足形成射影，第三步直线与所形成的角即为线面角。最后在练习中，按照这样的步骤与学生一起寻找线面角，在练习中熟悉这个程序性步骤。

附件：导学案

2.3.1 直线与平面垂直的判定（二）

——直线与平面所成角

【学习目标】

1. 了解平面的斜线的定义，理解射影的概念

2. 掌握直線与平面所成角的概念，并会求直线与平面所成的角

3. 培养学生的读图、作图的能力，培养学生的空间想象力，渗透类比，降维等思想

【学习过程】

一、复习旧知

复习线面垂直的定义和线面垂直的判定定理

二、探究新知