基于A星算法的移动机器人路径规划应用研究
2020-07-04周宇杭王文明李泽彬代宇浩徐宇豪柳晨阳
周宇杭 王文明 李泽彬 代宇浩 徐宇豪 柳晨阳


摘要:移动机器人路径规划一直是一个比较热门的话题,A星算法以及其扩展性算法被广范地应用于求解移动机器人的最优路径。该文在研究机器人路径规划算法中,详细阐述了传统A星算法的基本原理,并通过栅格法分割了机器人路径规划区域,利用MATLAB仿真平台生成了机器人二维路径仿真地图对其进行仿真实验,并对结果进行分析和研究,为今后进一步的研究提供经验。
关键词:移动机器人;路径规划;A星算法;栅格法;MATLAB
中图分类号:TP18 文献标识码:A
文章编号:1009-3044(2020)13-0001-03
1背景
路径规划是指在依靠特定的策略方法,符合一定的性能指标的前提下,从预先设定的起始点到达指定的目标点所形成的最佳路径。随着科技水平的不断提高,路径规划技术得以在很多领域中广泛应用。如小到游戏程序设计,大到巡航导弹的轨道路径;从农业中的田地精确测绘,到工业机器人设计;车辆道路行驶的GPS定位,室内扫地机器人路径规划,无人机的无障碍自主飞行和城市道路精准网格规划。至此,随之衍生出各种路径规划方法,其中包括传统算法和智能算法。由于传统算法所需的内存比较大,储存的空间也比较大,随着数目增加,实施难度将会逐步增大。为了更好地研究路径规划问题,专注于智能算法,对其进行不断研究和改进,从而能够催生出新的智能算法。比较常见的智能算法有遗传算法、人工势场法、蚁群算法等。路径规划也有多种分类,可以根据机器人对当前环境信息掌握以及障碍物的情况,可以分为如下几种情况:
1)机器人已经提前被告知周围的环境信息以及障碍物随机放置,处于静止不动的情况下,移动机器人做出相应的路径规划;
2)机器人了解了当前的环境信息以及障碍物不断更新的情况下,做出合理的判断;
3)机器人对于构建的环境信息处于未知但已知障碍点的情况下,进行合理的路径探索过程;
4)机器人对于障碍物以及环境信息都未了解情况下,对结果进行精确的规划。
也有机器人对当前环境的信息掌握程度的不同,可分为以下情况进行讨论:
1)机器人先一步一步将环境信息检验完成后,再对于总体的路径进行合理规划;
2)依靠相关的传感器进行机器人的局部路径规划。(例如ROS机人,通过激光雷达对于障碍物信息得以确定)
笔者则是从A星算法人手,A星算法是一种典型的启发性搜索算法,在人工智能方面应用广泛。而笔者建立的环境信息中,障碍的位置是随机变化的,如同上述分类中2),搜索出来的路径,最后比较得出效率最高的最优路径。
2环境模型的建立
为了大致模拟机器人的工作环境且不考虑机器人的大体形状,所以就决定构建一个二维平面环境。为了精确模拟机器人所在区域的具体位置,采用栅格法,通过划分形状大小相等的区域,根据所设计的二维平面环境,确定机器人的工作空间区域大小,从而确定区域之中栅格的数目,保证机器人可以自由行走在已设定的环境中。用直角坐标系把已分割好工作空间在MATLAB中表示出来,最终将整个机器人可行走的区域划分成12*12的栅格,同时将机器人和障碍物用分别用x,v形成的二维坐标来表示,图中障碍物用黑色圆点来表示,其他空白未标记的位置为机器人可以行走的区域空间。
3基于栅格图下A星算法的路径规划
3.1 A星算法思想
A星算法是一种启发性的算法,即由通过设定评估函数,全面性地对网格的各个节点进行评估。而每个节点就是机器人所到达的位置,对每个位置点都进行智能化评估,找到最好的位置,从而最终找到目标位置。A星算法评估函数如下:
其中,F(n)是一种对总过程节点的评估函数,表示从起始节点到目标节点的总的估计代价,G(n)是表示在特定状态空间下,从起始节点到达下一个节点的实际代价;H(n)是预测从当前节点到达目标节点的大致需要多少代价的最佳路径的估计值,最短路径(最优解)的关键在于选取代价函数,所以将其视为核心问题。对于预估启发方法,通常选用曼哈顿预估方法,该方法在A星算法中较为常见使用,比较容易人手。
其中D为曼哈顿距离,ab为下所属的矩形面积
常见的A星算法在扩展当前节点的周围节点一般采用八邻域法,即一次同时扩展当前节点周围八个点。在栅格图下,扩展节点图有前后左右表示如下:
3.2曼哈顿距离
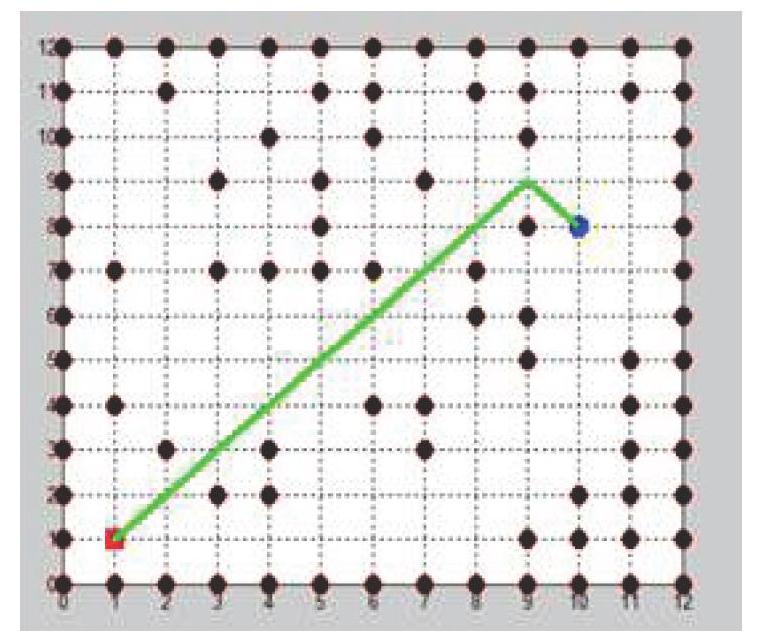
曼哈顿距离可以大概描述为在一个矩形区域间,某一点到达另一点距离是近似等于南北方向的垂直距离与东西方向上垂直距离之和,但是曼哈顿距离不是处于固定值,随着节点的变化,曼哈顿值也会随之进行相对应的变化。图3中黑色曲线表示A节点到B节点的实际距离,黄绿色线代表欧式距离(AB直线距离),红色线是曼哈顿等价距离。
3.3 A星算法初步过程
首先对于搜索区域进行简化成一组可量化的节点,节点可以适应于不同类型的区域之中,因为在划分搜索区域时,不仅仅是标准的矩形,可能是其他多边形,所以此时用节点代替多边形的某一区域则更准确和可靠。其次A星算法在执行时,会创建两个列表,一个列表叫Open list(开放列表),另一个列表叫Close list(封闭列表)。将未扩展的节点放人Open list中存放,而将已扩展完的节点存放到Closelist中。在Openlist中,将列表中节点根据F值的大小,按照从大到小的顺序进行排列,找到F值中的最小一个,并从Open list中删除,将其添加到Close list中。由于起点只有唯一存在的节点,将它放入开放列表,同时让其作为当前节点,通过当前节点搜索邻近八个扩展节点,最后将起点放人封闭列表。如果这些节点不在开放列表中,则将这些扩展节点全部添加到开放列表中,并根据F值的大小,按照上述操作过程,选出F值最小的节点,添加到封闭列表,作为当前节点,并按照此情况继续搜索其余节点;如果这些扩展点在开放列表中,那么在扩展的节点的开放列表中,令当前节点为父节点,路径中所设计的代价函数将对这个节点进行评估,并且重新计算该节点的G值,与之前的G值进行比较,选择出G值最小,作为当前节点的G值,再对F值进行重新计算,依次排列,循环上述搜索步骤,直至找到目标,将目标点添加到开放列表中,将开放列表中的各个节点逆序排出,从而得到一条搜索路徑,即为最佳路径(最短路径)。
A星算法作为一种典型的启发性搜索算法,常常对其进行改进和优化,使在路径规划算法中更富有效率。通常在路径规划中,它不需要把所有的节点都一一搜索出来,速度非常快,但同时,它对于路径规划中机器人移动存在代价预测,所以有的时候会出现搜索不到最适路径,这是其局限性。
3.4 A星算法实施流程图及步骤
具体实施步骤如下:
1)进行初始化过程,生成一个存在障碍物环境,机器人对最初环境进行识别判断。
2)随机添加40个障碍物,判断障碍物与之前障碍物是否有重复,如果有重复则重新添加。
3)机器人通过A星算法,识别出各个节点F值,判断是否是可行点,如果是则将其添加到开放列表中。
4)机器人首先生成一条路径,最后达到目标点,再将开放列表中的点逆顺遍历,最后判断是最佳路径,如果是将路径显示出来,不是的话,将显示未搜索到合适路径。
4实验仿真与分析
4.1MATLAB环境建模
利用栅格法精确分割12*12方格作为机器人的路径规划的实验区域,为了减小不必要的误差,实验中将移动机器人、目标点以及障碍物不考虑具体形状和大小均看作质点,通过利用X,Y组成的二維坐标一一对应精确表示质点在所显示地图上的实际位置。随机设置生成障碍数是40个,设置起始点坐标start[1,1],设置目标点坐标goal[10,8]。有限面积范围为11*11,生成边界以及可视范围。在MATLAB软件中,设置相关的基本元素,使障碍物、移动机器人和目标点的颜色,形状各不相同,便于区别。(障碍物是黑色实心圆点,是红色实心圆点,障碍物是蓝色实心)
如图5、图6所示,依据障碍物的随机设置,在相同的基本的元素下,会出现不同地图形式,可以获得不同的最佳路线。
4.2运行仿真
通过MATLAB仿真软件调节进行程序运行。利用曼哈顿距离公式推算相应的G值,计算各个时刻的F值,从而使移动机器人顺着G值最小的点进行移动,最后到达目标点位置。
在二维平面下的有效范围内,移动机器人的起始点的坐标为[1,1],运动方向存在八个方向,随机生成的40个障碍物,方向速度均为静止。如图6所示,用平滑的曲线连接各个点,得到最佳路线。
4.3实验数据分析
如表1数据可知,在随机放置40个障碍物的地图中,移动机器人移动路径长度及最大偏角不同,其算法的消耗代价也不相同。对于传统A星算法,只是简单地考虑到对于F值大小的如何判断,而没有过多的深入研究,可能会存在在可行区域内机器人会出现搜索不到目标的情况。另外对于偏角的过大也应该注意,为了使机器人能够无碰撞地进行路径探索,对于H(n)这个代价函数进行合适的分析以及设计就显得很重要,在实际路径规划中,才能使得移动机器人更能成功寻找到最佳路径。
5结束语
通过栅格法构建的移动机器人的二维平面模型,利用A星算法的启发性特性,搜索速度快的特点,很好解决机器人在规划好的二维平面环境中,随机放置静态障碍物时,移动机器人能在无碰撞状态下,通过估计最小代价来寻找最佳路径的问题。在已建立的环境中设置基础信息,利用曼哈顿公式,计算对角距离,从而确定G值和F值,移动机器人通过起始点沿着G值最小点来寻找目标点。在MATTJAB软件下,建立相对应的环境,实验结果表明该方法在二维平面环境中可以在有障碍物情况下尽可能找到一条最佳路径(最短路径)。同时,还存在搜索不到合适路径的时候。在之后的研究中,还需要解决的问题,尽量使得算法更加便捷和精准。
