创新投入、政府支持与区域创新——基于创新价值链的视角

王淑英，常 乐

（郑州大学管理工程学院，河南郑州 450001）

知识经济时代背景下，科技创新已成为提升竞争力的核心，也是实现经济可持续发展的重要支撑。区域创新是我国创新的重要组成部分，主要由R&D投入来推动。根据我国的《2017 年全国科技经费投入统计公报》，2017 年我国R&D 经费投入总量为17 606.1 亿元，位居世界第二，同时R&D 投入强度已达到中等发达国家水平，政府投入力度持续加大、政策环境进一步改善。然而与发达国家相比，我国整体研发水平仍然存在大而不强、多而不优的情况。《2019 年国务院政府工作报告》也指出我国自主创新能力不强，关键核心技术短板问题凸显；习近平总书记强调核心技术一定要掌握在自己手中。因此，我国的创新资源是否实现了有效配置，创新投入是否能有效提高创新能力、促进创新产出、提升创新绩效，成为极具现实意义的研究问题。同时，由于创新活动的强正外部性和高风险的特质，各创新主体依靠R&D 资源自发进行的创新活动可能会造成竞争无序和市场失灵问题，这为政府对区域创新的参与提供了理论和现实基础［1］，因此将政府支持纳入区域创新的研究有重要的实践意义和学术价值。综上，本文基于创新价值链视角分析创新投入、政府支持对我国区域创新的影响，力求以新的视角探讨我国区域创新效率不高的问题，并给出对策建议。本文可能的创新点在于：（1）从创新价值链的视角出发，将创新过程分为两个阶段，并考虑经济变量的空间依赖性，运用空间计量经济学模型分别探讨创新投入、政府支持对区域创新两阶段的不同作用；（2）在政府科技投入方面，大多研究基于微观或中观视角研究创新投入与企业、产业创新的关系，但对于区域创新以及不同阶段区域创新的研究较缺乏，基于此，本研究将在现有研究基础上进行拓展。

1 文献综述

创新是经济可持续发展的第一动力，国家创新能力的提升依赖于区域创新的发展，增加研发投入是提高区域创新水平、促进区域经济增长、提升区域竞争力的重要战略举措［2］。智力资源和研发资本是影响区域创新绩效的直接因素［3］，与创新相关人员和资金的投入都对区域创新能力的提高产生直接的影响。近年来，学者围绕创新投入对创新能力的影响作用展开了不同程度的讨论：部分研究认为创新投入能够有效促进创新，存在正相关关系，如Hong 等［4］从战略导向视角研究证明了高水平的创新投入能够提高产品的创新程度，直接促进创新产出；Escribano 等［5］基于知识流理论研究发现内部R&D 投资能有效扩展外部R&D 资源并刺激创新产出。另一部分学者认为创新投入对创新的作用并非简单的线性关系，而是存在二次效应，如Yeh 等［6］采用面板阈值回归模型研究发现R&D 投入强度与企业绩效之间在倒“U”型关系；Delgado-Verde 等［7］剖析了创新要素投入对企业突破性创新的影响，研究表明研发投入和社会资本对创新的影响存在二次效应。

科技创新的空间正外部性特征说明创新需要政府主导发展。目前国内外关于政府支持与创新关系的研究多集中在微观和中观层面，研究政府与企业创新的关系，但并未达成一致的结论。一部分研究认为政府支持可以有效促进创新：政府的研发补贴是政府引导企业技术创新的政策工具，可以有效促进企业的研发投资［8］，并通过企业R&D 资本投入的增加进而提高企业的研发能力［9］；同时，政府支持可以降低创新成本，提高企业的研发效率［10-11］，促进企业创新发展。另一部分研究认为政府支持对企业创新有一定的负向影响：政府的研发投入增加会对企业研发投入产生挤出效应、替代效应或取代效应［12-13］，改变企业对研发的投资行为，从而抑制企业创新绩效的提升，例如Michael 等［14］的研究证实了政府的R&D 直接补贴是无效的。国内关于政府支持与区域创新的研究也存在不同的结论，如汪辉平等［15］认为政府财政支出对区域创新有显著的正向促进作用；吴晓飞［16］利用省级面板数据的研究发现地方政府科技补贴强度与区域创新能力间存在较为明显的倒“U”型关系；然而，杨若愚［17］基于我国30 个省份的面板数据研究发现政府R&D 投入对区域创新绩效有负面影响。

综上所述，已有研究对创新投入、政府支持与创新的关系提供了一定的研究思路和基础，但是对二者对创新影响的方向尚未得出一致的结论；并且，现有研究相对缺乏对区域创新的阶段性产出的区分，实际上，不同阶段的创新存在异质性，同一方式的投入对不同阶段的创新产出的作用机制和影响效果不尽相同，因此有必要基于创新价值链的视角，从不同阶段考察创新投入和政府支持对区域创新的影响。本文将通过对2008—2017 年我国30 个省份面板数据的实证分析，着重考察创新投入、政府支持在创新两阶段中的差异化影响，为优化投入配置、提高政府支持效率提供一定的参考和借鉴。

2 研究假设

2.1 创新投入与区域创新

从生产视角看，技术创新是从创新要素投入到创新产品产出的一个多阶段、多要素的价值链传递过程，包括创新的投入、创新知识的凝结和创新成果的实现［18］。科技研发阶段是由创新投入到创新知识凝结的过程，成果转化阶段是从知识凝结到创新成果实现的过程，两个过程的产出形式不同、内涵不同，本文基于创新价值链理论分别对这两个阶段的创新进行研究。

2.1.1 创新人员投入与区域创新

人才投入对创新的作用包括直接作用和间接作用两种［19］。具体来说，研发人员不仅具备提升生产效率等可度量的显性价值，直接促进创新，而且科技研发人员的投入或流动会产生难以观测的隐形价值［20］，如通过知识的溢出、技术的转移等间接推动创新发展。潘娟等［21］从研发、成果转化、产业化、技术扩散四方面对创新进行投影寻踪降维处理，得出一维科技创新综合产出结果，发现R&D 人员对科技创新的提高具有正向的促进作用，且推动作用较明显。这证明了创新人员对创新综合能力的正向作用，但不同阶段创新产出有着不同内涵，需要对其分别进行研究。张凤兵等［22］基于山东省认定的省级高新技术企业数据的研究表明R&D 人员的投入对专利产出存在显著的正效应，而专利等作为科技研发阶段的创新产出［23］，其水平的提高为成果转化提供了支撑和保障，可促进成果转化阶段的创新产出，因此创新人员的投入可通过知识和技术的转移推动成果转化创新产出。基于此，本文提出如下假设：

H1a： 创新人员投入对科技研发创新产出起到促进作用；

H1b：创新人员投入对成果转化创新产出起到促进作用。

2.1.2 研发经费投入与区域创新

研发资金的投入可以带动区域提高技术水平、生产效率以及管理能力，进而通过技术溢出路径提升创新效率［24］，刺激创新能力的提升。如在科技研发阶段，Hall 等［25］通过对加拿大生物技术行业的研究发现研发投资对专利相关的创新有更直接的正向影响，而创新投入规模的扩大可能逐渐显现出边际产出递减效应［26］；何涌［27］以2009—2016 年我国创业板上市公司为样本，使用面板数据进行研究发现，过多的R&D 经费投入会降低创新质量，造成资源的冗余和浪费。而在成果转化阶段，对新知识、新技术等这类创新中间阶段产出的成功转化需要大量研发资金的投入，若在转化期间的投入未达到一定水平，可能会出现投入的资金打水漂的现象，不仅不能有效促进研发成果的转化，可能还会由于人才、知识、技术等要素的流失对成果转化阶段的创新产出产生抑制作用。基于此，本文提出如下假设：

H2a：研发经费投入对科技研发产出具有倒“U”型影响；

H2b：研发经费投入对成果转化创新产出的影响呈“U”型分布。

2.2 政府支持与区域创新

目前大多研究基于微观或中观视角研究政府科技创新投入与企业、产业创新的关系，例如刘虹等［28］以我国上市公司2007—2009 年的数据为样本进行了实证研究，结果发现政府补贴在投入初始阶段会对企业R&D 支出起到显著的促进作用，但这种激励效应会随着政府补贴力度的增大而减弱，当超过最优补贴值后，政府补贴会对企业R&D 支出产生挤出效应。对于区域创新而言，无论是科技研发阶段还是成果转化阶段，由于创新的高风险特性，政府在初期对创新的支持可以降低创新投入风险，激发创新人员的积极性，提高创新成果研发和转化成功的概率，但政府的科技补贴不可能无限度地发挥作用，其补贴资金也会面临边际报酬递减问题［16］，当政府支持达到一定规模时，若继续加大支持力度，可能会对各创新主体自身的研发投资产生挤出效应，导致区域创新产出的下降，进而影响区域创新的发展。基于此，本文提出如下假设：

H3a：政府支持对科技研发创新产出存在倒“U”型影响；

H3b：政府支持对成果转化创新产出存在倒“U”型影响。

3 研究设计

3.1 研究方法

3.1.1 空间相关性分析

（1）空间自相关性检验。空间自相关性检验用以衡量区域某一指标的空间特性，其检验方法主要有莫兰指数（Moran'sI）和吉尔里指数（Geary'sC），本研究采用较为常用的莫兰指数进行测度，取值范围在［-1，1］之间。莫兰指数大于零表示正相关，小于零表示负相关，接近零时则表明该测量指标相邻区域独立不相关，呈现随机分布；其绝对值越大，表明所检验指标变量在相邻区域的空间相关性越强。莫兰指数的计算公式为：

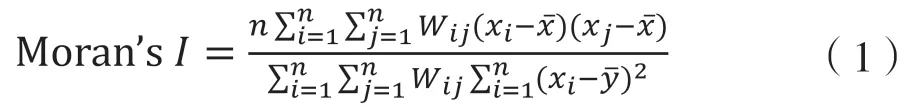
式（1）中：xi、xj分别为空间单位i和空间单位j的指标值；Wij为空间权重矩阵空间单元的相应元素。

（2）空间权重矩阵。进行空间计量分析的前提是度量区域间的空间距离，即建立空间权重矩阵（spatial weighting matrix）。最常用的距离函数为“相邻（contiguity）”，即如果区域i与区域j有共同边界，则ωij=1；反之则ωij=0。本文采用一阶Rook 矩阵作为研究的空间权重矩阵。

3.1.2 空间计量模型

随着地理学第一定律的提出，空间效应已被广泛引入到经济学领域的研究中，由于经济现象间存在着某种程度的空间联系，使得空间计量模型比传统计量模型的解释力更优。空间计量模型主要分为空间误差模型（spatial errors model，SEM）、空间滞后模型（spatial lag model，SLM）和空间杜宾模型（spatial Durbin model，SDM）3 种。其中，空间误差模型在经典线性回归模型中考虑了随机误差项的空间依赖性，引入误差项的空间滞后项，模型表达式为：

式（2）中：Y为被解释变量矩阵；X为解释变量矩阵；ε为随机误差项向量；μ为服从正态分布的随机误差项向量；ρ为空间误差自相关系数；W为空间权重矩阵；β为解释变量的回归系数。

空间滞后模型在经典线性回归模型的基础上引入空间自回归系数（spatial auto-regressive parameter），用以度量因变量空间滞后项的影响，模型表达式为：

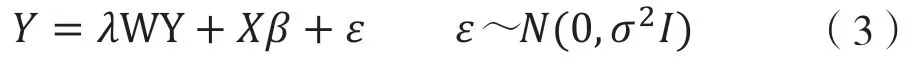
空间杜宾模型是在空间滞后模型中引入解释变量的空间滞后项，考虑邻居自变量和因变量的空间依赖性，模型表达式为：

式（4）中：WXδ为邻居自变量的影响，δ为相应的系数向量。

3.2 指标选取

（1）被解释变量。创新贯穿了从资源投入到科研成果输出、再到实现科技成果转化的全过程，一方面创新投入为区域科技知识创新提供保障和动力，另一方面通过创新要素的投入和科技成果的转化提高创新成果的应用价值，增加区域经济产出，因此本研究参考Hansen 等［29］、赵增耀等［30］的研究，基于创新价值链视角将创新过程分为科技研发和成果转化两个阶段进行分析。科技研发阶段的创新产出用国外主要检索工具收录的科技论文数和专利申请数来表示，成果转化阶段的创新产出用新产品销售收入和技术市场成交额表示。对各绝对数变量进行对数变换，对数形式不会改变数据间的原始关系，同时能够消除数据在时间序列中存在的异方差并使其趋势线性化。各指标权重的设定采用等权法确定［31］。

（2）核心解释变量。根据经典的知识生产函数，投入要素包括劳动要素和资本要素投入，作为创新活动的基本组成部分，R&D 资源在创新过程中起着关键的作用。国内学者在进行创新研究时，一般选取R&D人员和R&D经费作为创新的投入指标，因此本文中创新劳动要素用R&D 全时人员当量来描述，创新资本要素用R&D 经费内部支出来表征。对于区域创新而言，政府对创新支持最直接的手段应属财政支出中的科技支持力度［32］。我国2007 年对财政收支分类体系改革的目的是为了按照经费功能进行管理，类级指标反映了政府职能活动［33］，在政府用于公共支出的预算中科技占比越大，说明政府部门对科技创新的重视程度越高，因此本文采用财政支出中科技支出占比来表示政府对创新的支持。同样的，对绝对数变量进行对数变换。

（3）控制变量。根据既有文献，本文选取影响创新产出的其他变量包括各地区的经济发展水平、人力资本水平、对外开放程度和产业结构。其中，经济发展水平用人均地区生产总值（GDP）来描述，人力资本水平用大专及以上人口数占6 岁及以上人口比重来衡量，对外开放程度用进出口总额与GDP比值来表示，产业结构用第三产业增加值与第二产业增加值之比来测度。

3.3 数据说明

考虑到创新投入产出的滞后效应，本文中创新产出均采用滞后1 期的观测值。选取2008—2017 年我国30 个省、自治区、直辖市（由于部分数据缺失，因此未包括西藏和港澳台地区）的面板数据（以下简称“样本”）进行分析，各省份原始数据均来源于2009—2018 年的《中国统计年鉴》和《中国科技统计年鉴》。具体如表1 所示。

表1 样本变量说明

4 实证分析

4.1 区域创新的空间相关性检验

采用一阶Rook 矩阵作为空间权重矩阵，计算2008—2017 年样本区域创新两阶段产出的莫兰指数如表2 所示，各样本省份创新产出的莫兰指数均在0.23～0.31 之间，且均通过了1%水平上的显著性检验，说明我国省域两阶段的创新产出均存在空间正相关，表明我国创新产出在空间上存在显著的溢出效应，创新能力高的区域会对其周边地区产生辐射效应。因此，说明采用空间计量模型来对样本变量进行分析更为合适。

表2 2008—2017 年我国区域创新两阶段产出的莫兰指数值

4.2 空间计量模型选择

莫兰指数和莫兰散点图直观地显示出区域创新产出具有显著的空间自相关关系，故需建立空间计量模型对区域创新进行分析。为选择合适的空间面板模型，可根据拉格朗日乘数检验（LM）、似然比检验（LR test）来进行判断。对非空间效应的面板模型进行检验，结果如表3 所示。其中，模型（1）至模型（4）为科技研发阶段的混合估计、空间固定效应、时间固定效应、双固定效应下的检验结果；模型（5）至模型（8）为成果转化阶段的检验结果。

表3 样本数据非空间面板模型检验结果

根据似然比检验结果，样本数据的时间固定效应和空间固定效应均通过显著性检验，表明固定效应下的标准面板计量模型最优。根据拟合优度系数R2结果，双固定效应模型拟合度较差。根据LM 检验结果，固定效应模型的LM 检验均存在显著项，说明空间依赖性在该模型分析中不可忽视，需进一步考虑空间面板模型。接着本文采用Wald 检验和LR 检验进一步判断合适的空间计量模型。由表4 可见，两种检验都将空间滞后模型、空间误差模型与空间杜宾模型进行比较，其伴随概率均通过了5%水平上的显著性检验，说明空间杜宾模型较空间误差模型、空间滞后模型更具解释意义，因此本文运用空间杜宾模型进行分析。

表4 样本数据的Wald 检验和LR 检验结果

4.3 实证结果与分析

首先，对创新的第一个阶段（科技研发）进行分析。由非空间面板模型的似然比检验结果可知，固定效应下的计量模型最优，同时未加二次项和考虑二次项模型的Hausman 检验统计量分别为49.186（P值为0.000）、41.336（P值为0.005），均在1%水平上显著，因此选取固定效应模型更加有效。如表5 所示，模型（1）至模型（3）分别为不加二次项的空间固定效应、时间固定效应和双固定效应下的空间杜宾模型检验结果，模型（4）至模型（6）分别为考虑自变量二次项的空间固定效应、时间固定效应和双固定效应下的空间杜宾模型检验结果。其中，模型的拟合优度系数R2均大于0.65，说明拟合较好，与其他模型相比，双固定效应空间杜宾模型的拟合优度系数R2更高、σ2较低，说明双固定效应回归的拟合优度较高，结果更有效，因此本文采用双固定效应空间杜宾模型进行分析。分析结果显示：（1）在未加入二次项时，R&D 人员影响不显著，而R&D 经费投入与政府支持均显著促进区域科技研发创新产出；加入二次项后，R&D 人员对科技研发创新产出的影响呈“U”型分布。这与假设H1a不符，可能的原因是创新人员具有团队性，当R&D 人员投入较少时无法体现科技研发人员的研发能力，只有加大人员投入、加强智库建设等，才能发挥科技研发团队的创新能力，呈现出对科技研发创新产出的正向影响力。（2）R&D 经费投入和政府支持对科技研发创新产出的影响呈倒“U”型分布，这验证了假设H2a和H3a，说明研发经费投入和政府支持都存在阈值效应，适度的经费投入和政府支持有助于推动区域科技研发创新产出。

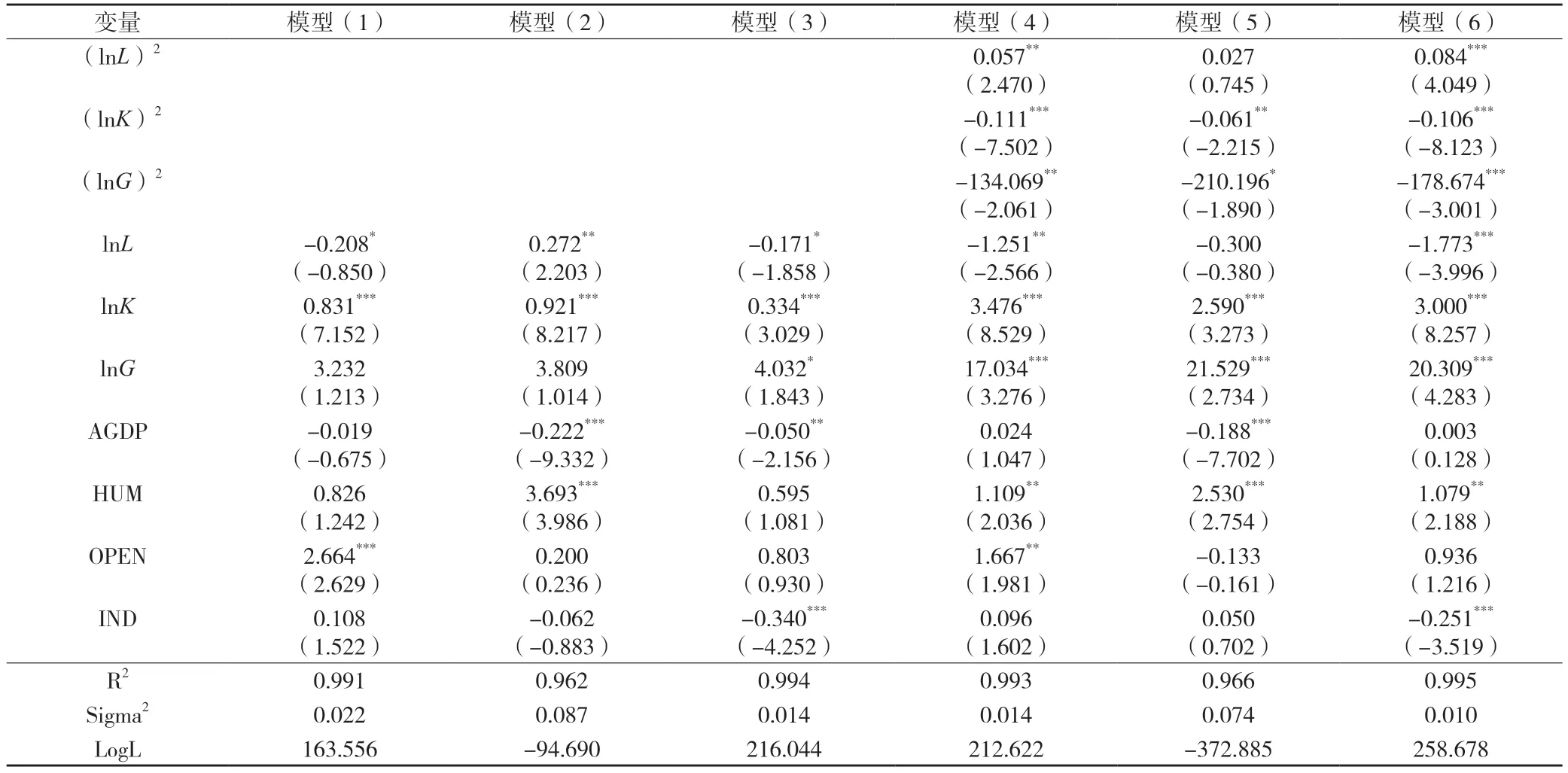
表5 2008—2017 年样本区域科技研发创新产出空间计量结果

其次，对于创新的第二阶段（成果转化）进行分析。考虑将第一阶段得到的创新产出代入模型中，作为成果转化阶段的解释变量，未加二次项和考虑二次项模型的Hausman 检验统计量分别为98.748（P值为0.000）、78.565（P值为0.000），同样的，采用双固定效应空间杜宾模型进行分析。如表6 所示，模型（1）至模型（3）、模型（4）至模型（6）分别为未加入自变量二次项和考虑自变量二次项的空间固定效应、时间固定效应和双固定效应下的空间杜宾模型。检验结果表明：（1）科技研发阶段的产出对成果转化阶段创新产出有显著的正向促进作用，而无论是否加入二次项，R&D 人员投入对成果转化阶段创新产出无显著影响，与假设H1b相悖。原因可能是R&D 投入重点关注研究与试验发展类型的创新，而创新人员投入的增加将创新工作的重心放在科技研发中，在一定程度上忽视了对现有成果的转化。（2）R&D 经费投入的平方项对成果转化阶段的产出水平呈非线性影响，正好验证了假设H2b，说明成果的转化需要大量R&D 经费的投入，当其投入水平未达到某一标准时，创新成果并不能实现有效转化和应用。（3）政府支持对成果转化阶段创新产出的影响呈倒“U”型分布，与假设H3b一致，说明科研成果是否可以成功转化、产生经济效益并为社会所用，与政府支持是分不开的，而政府支持与创新产出的关系存在阈值效应，并非越强越好，需探索促进成果转化最大效用值，避免造成资源的冗余和浪费。

表6 2008—2017 年样本区域成果转化创新产出空间计量结果

表6 （续）

4.4 稳健性检验

为增强研究结论的稳健性以及说服力，本文运用两种方法进行稳健性检验。经Hausman 检验，均应使用固定效应模型。其中，模型（1）至模型（3）为科技研发阶段的稳健性检验结果；模型（4）至模型（6）为成果转化阶段的稳健性检验结果。

首先本文采用t-1 期的投入与t期的区域创新进行了回归分析，投入产出滞后期可能会更长，因此用滞后两期的创新数据进行回归分析，主要变量的回归结果保持一致，如表7 所示。由表7 和表5、表6 的回归结果可知，在滞后1 期和滞后两期两种情形下，R&D 人员投入对科技研发创新产出的影响呈“U”型分布，R&D 经费投入和政府支持对科技研发创新产出的影响呈倒“U”型分布，同时政府支持对成果转化阶段创新产出的影响也呈倒“U”型分布。这充分证实了本文研究结论的可靠性及稳健性。

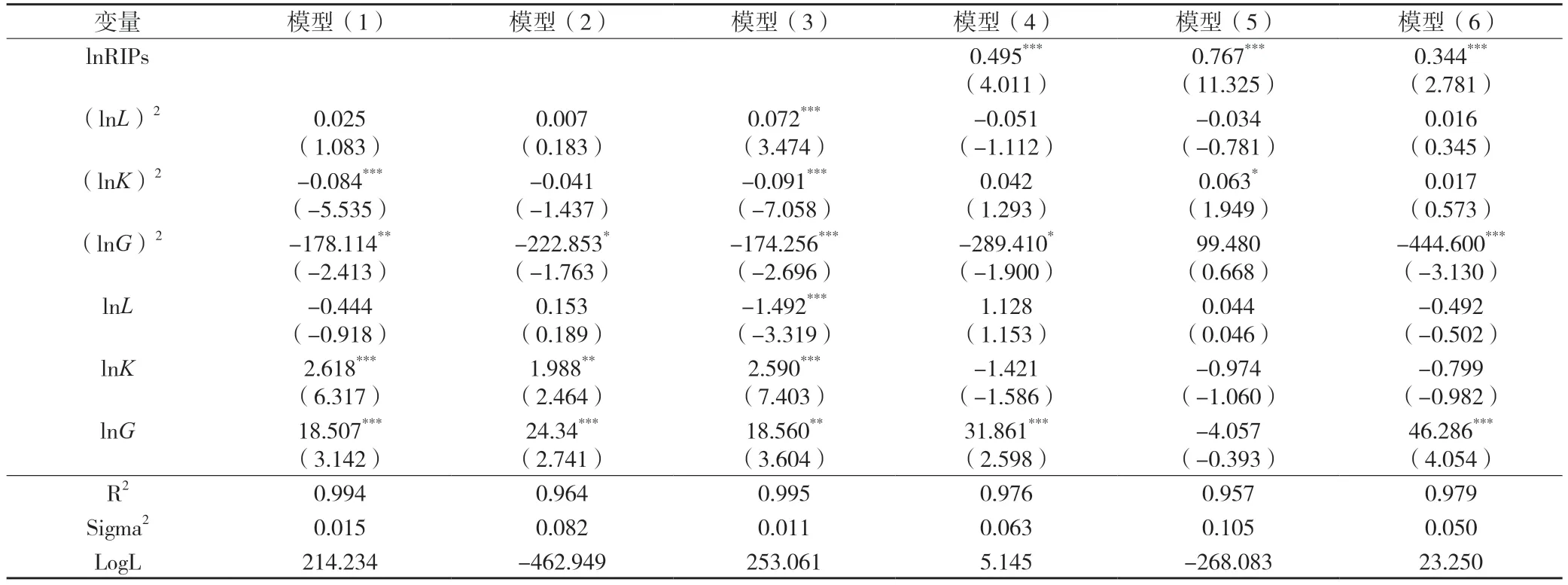
表7 2008—2017 年样本变量稳健性检验结果（更换滞后期）

其次，替换变量。在现有研究中对于创新产出的测度方法有很多种，本文进一步采用专利授权数替换科技研发阶段的产出变量，用规模以上工业企业新产品出口额替换成果转化阶段的产出变量再次进行回归分析，结果仍与前文研究结论基本一致（如表8）。由表8 和表5、表6 的检验结果可知，对区域创新无论采用单一变量还是综合变量测度，创新投入、政府支持对其的影响结果基本一致。这进一步验证了本文研究结果的可靠性和稳健性。

表8 2008—2017 年样本变量稳健性检验结果（替换变量法）

表8 （续）

5 结论与建议

本文基于空间计量经济学理论，采用2008—2017 年我国30 个省份的省级面板数据，从创新价值链的研究视角构建空间杜宾模型，实证分析创新投入、政府支持对区域创新不同阶段的影响。研究发现：（1）根据创新价值链视角，创新投入、政府支持在创新的不同阶段对区域创新的影响不完全相同；（2）在科技研发阶段，R&D 人员投入对区域创新的影响呈“U”型分布，R&D 经费投入和政府支持对区域创新的影响呈倒“U”型分布；（3）在成果转化阶段，对区域创新影响效果最显著的是政府支持，其影响呈倒“U”型分布，而R&D 人员投入对区域创新无显著影响，R&D 经费投入存在非线性影响（稳健性检验中经费投入对成果转化创新产出均无显著影响）。综上，本文提出以下政策建议：

（1）相关部门和研究学者应合理分析不同阶段区域创新的需求，精准把握科技研发、成果转化的特质及内涵，有目的、有计划、有侧重地投入创新要素，避免一概而论或以偏概全从而导致创新效率低下的问题。

（2）在科技研发阶段：一是由于创新人才性质的特殊性，靠单个或几个人才的投入无法有效发挥对区域创新发展的推动作用，只有不断加大创新人才的投入，形成高质量创新团队，才能对科技研发创新产出产生明显的促进作用，因此应建立完善的人才引进和激励机制，拓展引才渠道，加强人才培养和智库建设，凝聚团队智慧，加速创新发展。二是由于经费投入和政府支持存在阈值效应，不能一味盲目地加大经费投入，而应以国家战略为导向制定创新计划，完善经费管理办法，利用经验数据，基于边际效益递减规律合理分析实现经费边际效应为零的投入值，避免资源短缺或资源冗余，实现资源利用效率最大化。

（3）在成果转化阶段：一是由于政府支持存在阈值效应，因此政府应制定精准的投入计划，合理分析和把握对创新的支持力度，重点扶持创新弱势地区，构建因地制宜的政府支持系统，实现区域创新协调发展；同时，各地方应合理利用政府支持资金，根据创新不同阶段的需求合理分配对各阶段资源的投入，避免造成资源浪费。二是由于创新要素的投入在该阶段作用并不显著，因此应完善创新投入管理方法，优化创新绩效考核标准，建立有效的投入要素利用体系，避免出现“科研腐败”“一刀切”等情况；此外，进一步完善不同形式的产学研合作联盟，构建公平的薪酬保障制度，避免研发与转化脱节，有效发挥创新投入要素对创新的促进作用。