周期调制相互作用对Fermi-Pasta-Ulam-Tsingou模型热化进程的影响
2020-07-03李茹马丽娟张振俊
李茹,马丽娟,张振俊
(1. 南京高等职业技术学校,江苏 南京 210019;2. 河海大学 理学院,江苏 南京 210098)
0 引言
能量均分定理是联系系统温度及其平均能量的基本公式,其基本内容是:处在温度为T的平衡态的系统中,分子热运动的动能平均分配到每个分子的每个自由度上,每个分子的每个自由度的平均动能都是kT/2,其中k是玻尔兹曼常数。在本质上,能量均分定理是关于热运动的统计规律,是对大量分子的统计平均所得到的结果,可以用统计物理进行严格证明。其实,能量均分的来源一直是很多物理学家想要解决的问题。由N个原子组成的一维单原子链,其振动模为N个格波,这N个格波是相互独立的。因此,对于理想的线性原子链,如果初始时能量集中在某些格波上,不管经过多长时间的演化,能量是不会向其他模传输的,也就是不可能达到每个振动模上能量均分的状态。但是,如果在线性原子链中考虑非线性作用,是否可以使系统达到能量均分状态?如果可以,就可以解释能量均分的来源这一统计物理学中至关重要的问题。基于此考虑,并且依赖于计算机性能的快速发展,1950年,Fermi与Pasta, Ulam, Tsingou等人开展了第1个数值理论研究。他们研究了一维谐振子链耦合上3次方(α-FPUT模型)的势能相互作用或者4次方(β-FPUT模型)的势能相互作用后系统的能量传输性质。他们期待系统能够达到热化状态,也就是初始的影响将消失,每个模上的能量是相等的。但是,令他们意想不到的是,系统出现了能量向初始状态回流的现象,称之为“FPUT回流”现象。这一现象激发了广大学者近70年的研究,推动了非线性科学、混沌理论等的发展。
Zabusky等人基于对Korteweg-de Vries方程的研究发现,在连续极限下,FPUT模型可以约化到Korteweg-de Vries方程[1]。该方程是一个可积方程,有孤子解。稳定孤波(孤子)在普通的初始条件下产生,通过介质传播,和其它孤子相互作用,不会改变自身性质。这给了FPUT模型的回流现象一个较合理的解释。1982年,Fucito等人提出了亚稳态观点[2]。他们认为FPUT在能量传输的过程中出现了亚稳态现象,即从某个初始条件出发,经过较短的时间,系统会达到一个相对稳定的状态。处在这个状态时,能量在一些模之间来回传递,也就是Fermi等人观察到的“FPUT回流”现象。然而,这个状态只是暂时的,长时间的动力学演化最终会使亚稳态向能量均分的状态转变。近些年来,可积的Toda模型也被用来与FPUT模型的动力学行为作比较[3-5]。研究发现,在弱非线性作用下,FPUT模型的动力学行为在较短的时间与Toda模型非常的相似[5],这可以用KdV理论解释。演化时间足够长之后,FPUT模型的运动轨道就会与Toda发生变化,亚稳态会破坏,FPUT模型最终会达到均分状态。
还有一种想法是从能量阈值的角度对FPUT模型的动力学行为作出解释。根据混沌理论,一个有若干自由度的非线性系统的运动可以显示出混沌行为,可以用常规的统计力学来描述。Izraielev等人猜测该系统存在一个能量阈值[6],超过该临界值,Kolmogorov-Arnold-Moser轨道将被破坏,系统将处于混沌状态,能量可以传递到其他模上并最终达到热化状态。在此基础上,他们给出了能量传输的机制。非线性可以调制本征模的频率,非线性越强,对频率的调制作用越大。当非线性强度超过某个临界值后,会造成不同本征模之间的频率部分重叠,从而造成不同模之间的共振现象,能量就可以通过这种共振现象从初始激发的模传到其他模上,最终达到热化状态。在强非线性作用下,也就是能量超过阈值的FPUT系统的热化现象已经被一些数值实验所验证[7-9]。但是,在任意小的非线性作用下,FPUT系统能否达到热化状态依然是一个充满了争议的问题。近些年来,对这一问题的一些尝试也已经开始[10-13]。基于共振波-波相互作用理论,Onorato等人认为,对于任意小的非线性作用,α-FPUT模型[10]和β-FPUT模型[11]可以通过非平庸的共振传递能量,并最终达到热化状态。如果非平庸的n波共振存在,那么能量均分时间teq与系统能量E之间应满足如下的标度关系:。对于FPUT短链,他们通过推导发现,最低阶的非平庸共振是六波共振。基于六波共振,他们从理论上得到了能量均分时间teq与系统能量E之间应满足如下的标度关系:。该标度关系已经被他们的数值结果所证实[10,11]。
以往对FPUT模型热化性质的研究都是基于均匀相互作用的情况,该项目将研究弱非线性作用下,周期调制的相互作用对FPUT模型热化进程的影响。通过该研究,可以掌握周期调制的相互作用对该系统的能量传输性质的影响,从而加深对FPUT系统能量传输机制的理解,具有一定的理论价值。
1 研究的模型和数值算法
研究的模型的哈密顿量如下:
(1)
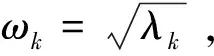
该项研究采用SABA2C偶对算法[14]研究系统的动力学性质。下面对该算法做简单的介绍。考虑一个由N个粒子组成的哈密顿系统:
H(q1,q2,…,qN,p1,p2,…,pN)=h=const
(2)
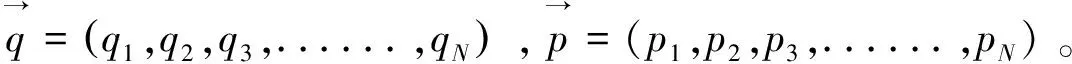
该系统2N维相空间的运动轨道可以由如下矢量表示:
(3)
其中xl(t)=ql(t),xl+N(t)=pl(t)。
(4)
哈密顿运动方程即可以用如下形式来表示:
(5)
LH为微分算符,它的定义为:
(6)
(7)
将系统的哈密顿量表示为:

(8)
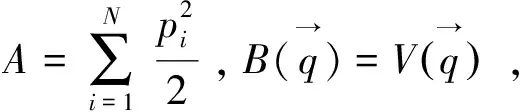
(9)
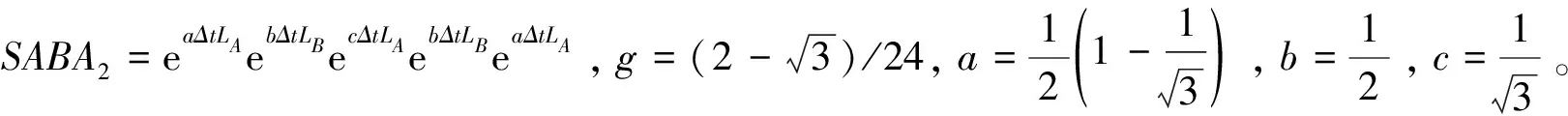
该项研究取N=32。初始时刻,将能量给予频率最低的本征模,固定α=0.33,计算的步长取Δt=0.1。这个步长保证在我们研究的时间尺度内,系统的相对能量误差小于10-5。进一步减小步长,对结果没有影响。
2 数值结果
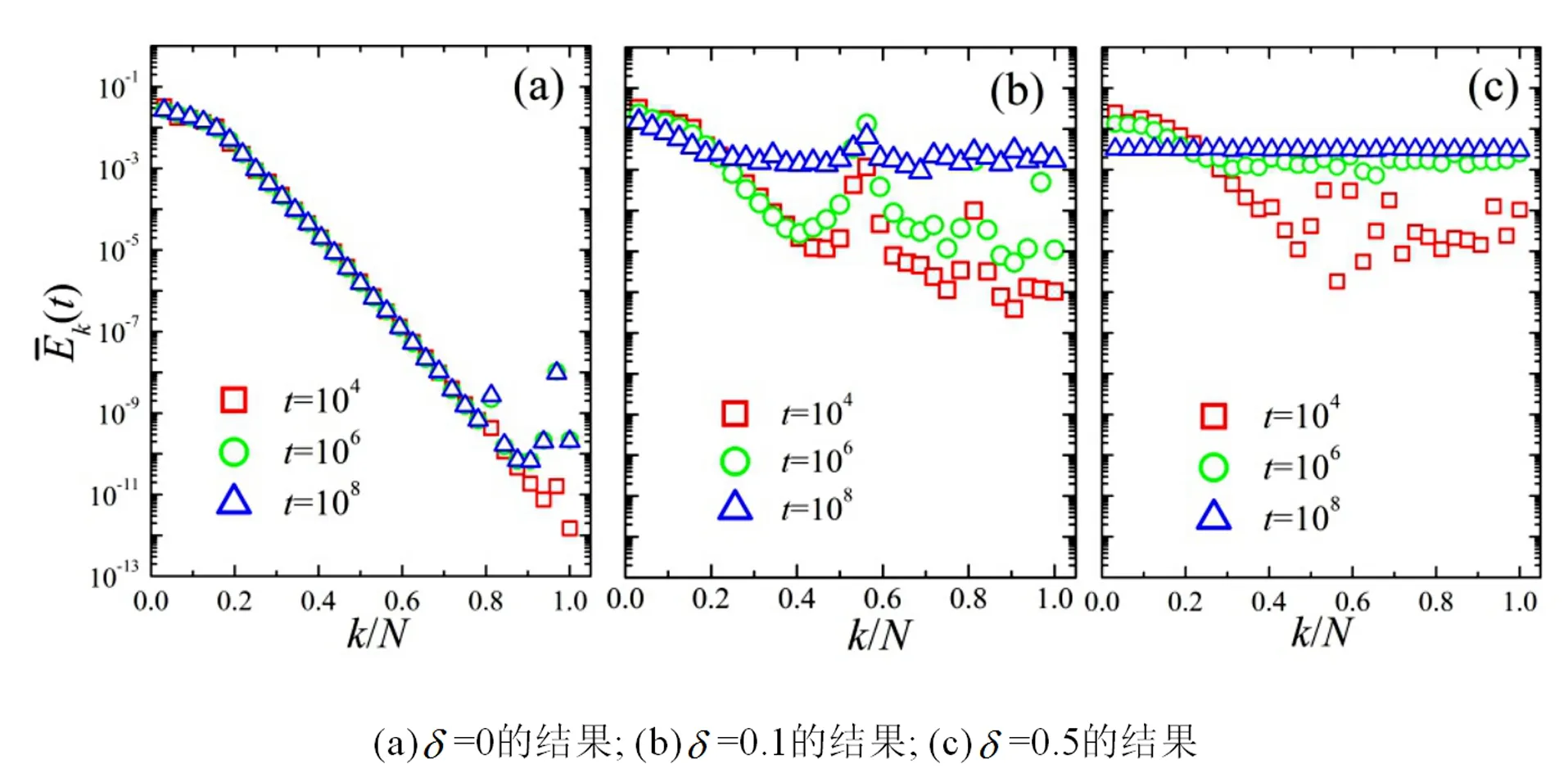
图1 不同时刻与k/N的关系
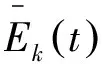
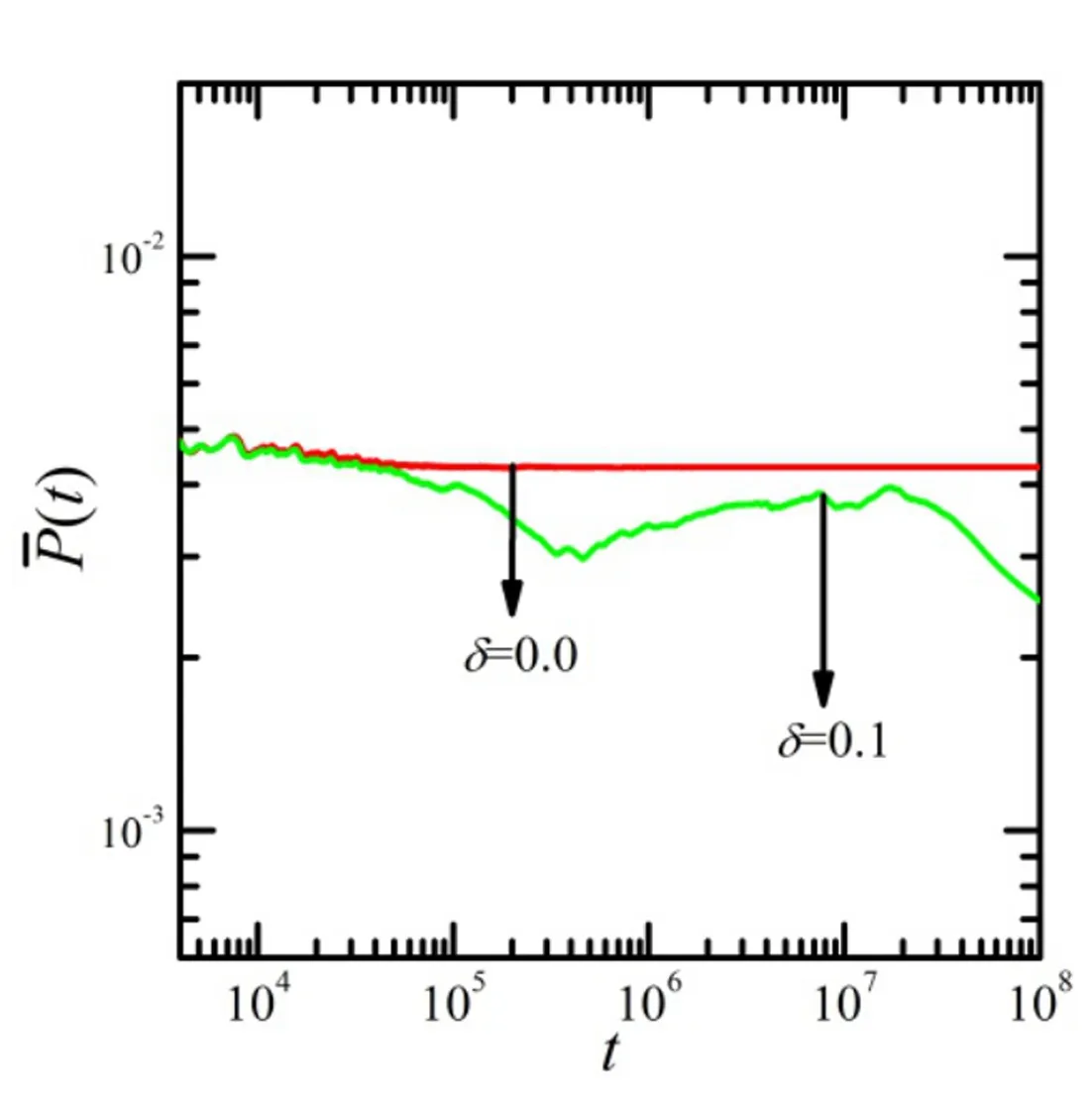
图随时间变化的结果
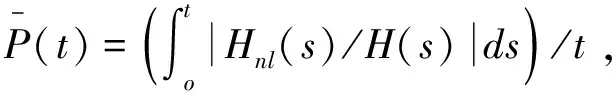
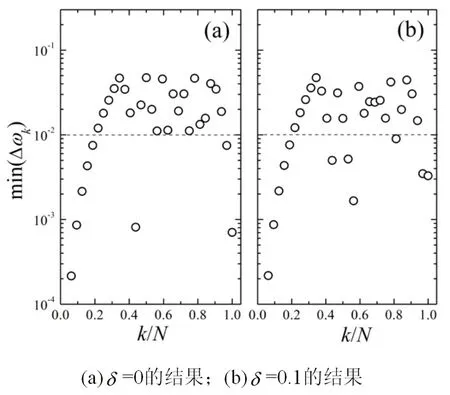
图3 min(Δωk)的值随k/N变化的结果
这是由于周期相互作用增加了与基频模ω1发生共振的本征模的数量,从而加快了热化进程。为了验证这一猜测,对频谱进行系统的分析。该项研究计算了jω1与ωk之间的差值,其中j的取值从2到N。将与ωk差值最小的结果定义为min(Δωk),这个差值越小,说明越容易与基频模共振。图3所示为不同调制强度下,min(Δωk)的值随k/N变化的结果。图3(a)给出了δ=0的结果。从图3(a)中可以看到,频率较低的一些模极易与基频模共振,这也是为何开始时能量可以向这些低频模传输的原因。图3(b)给出了δ=0.1的结果。从图3(b)中可以看到,除了频率较低的一些模容易与基频模共振外,频率较高的一些模也容易与基频模共振。如果以10-2划一条参考线,就会发现δ=0.1时容易与基频模共振的模数要明显大于δ=0。这就造成了周期调制可以加快热化的进程。另外,从图3(b)中还可以看到,k=17、18、26、31这几个模更容易与基频模共振。对照图1(b),发现这几个模上的能量传递确实比其他模更快。这也证明了能量可以通过与基频模的共振传递这一猜测的正确性。
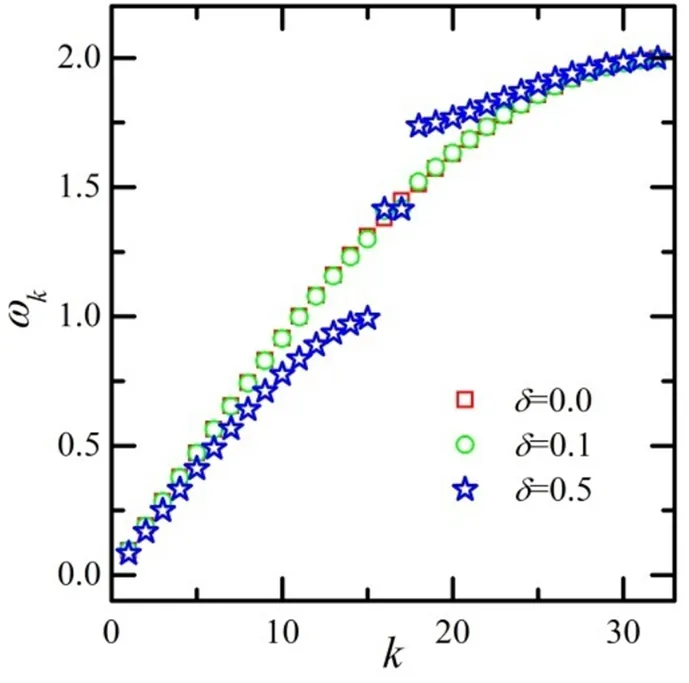
图4 δ取不同值时的线性本征频谱
下面解释另外一个问题,为何增加周期调制的强度可以加快热化的进程。在非线性强度不变的情况下,相邻本征模的频率之间的差别如果变小,共振就容易发生,且差别越小,共振越容易发生,热化也就越容易达到。为此,计算了δ取不同值时的线性本征频谱。图4所示为δ取不同值时的ωk的值随k变化的结果。从图4中可以看到,随着δ值的增大,相邻模的频率间的差别在减小,共振变得更加容易发生,从而造成了热化进程的加快。
最后,本文研究了不同强度的周期调制对热化时间teq与系统能量E之间标度性质的影响。为了描述热化性质,定义了如下物理量[26]:
(10)
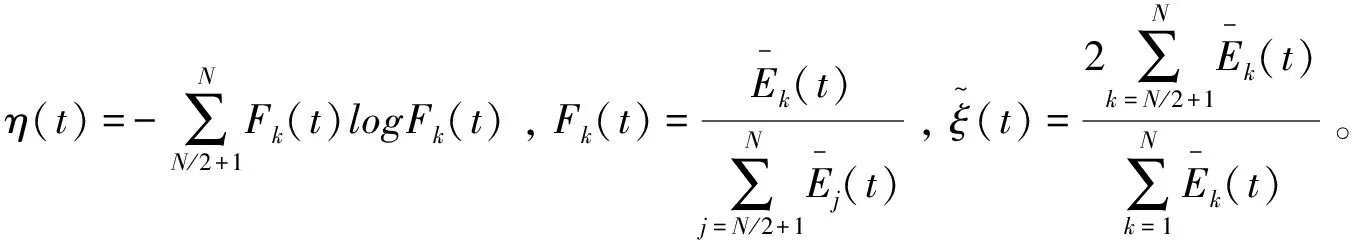
如果系统达到了热化状态,这个物理量应该等于1。图5所示为δ=0.5时,取不同的能量E时,ξ(t)随时间变化的结果。图5(a)中,从左至右分别是E=0.06, 0.04, 0.03, 0.025, 0.02和0.0185时,ξ(t)随时间变化的结果。从图5(a)可以看到,在研究的能量范围内,ξ(t)的值都从0逐渐趋近于1,也就说在研究的能量范围内,系统最终都可以达到能量均分状态。另外,随着能量的降低,热化所需要的时间也随之增加。这是由于随着系统能量的降低,非线性的强度也会随之降低,通过共振传输能量的速度会变慢,最终导致热化所需要的时间增加。图5(b)是将不同能量的曲线通过重新标度移到一起的结果。从图5(b)中可以看到,只要ξ(t)大于0.4,曲线基本上是重叠在一起的。也就是说,只要取ξ(t)大于0.4,热化时间teq与系统能量之间的标度关系与ξ(t)的取值无关。该项研究取ξ(t)=0.5所对应的时刻为teq。下面研究热化时间teq与系统能量之间的标度关系。图6所示为δ取不同值时热化时间teq与系统能量E之间的关系。从图6中可以看到,对于不同的δ,在一定的能量范围内,teq与E均满足如下的幂律关系:teq~E-4.0。这个幂律关系与文献[10,11]中得到的结果相同。说明在周期调制的FPUT系统中,非平庸的六波共振依然存在。但是,随着能量的进一步减小,这个标度关系就不再成立了。这个现象在文献[10,11]中并没有看到,说明在更小的非线性作用下,周期调制的FPUT模型中,非平庸的六波共振不再起作用。
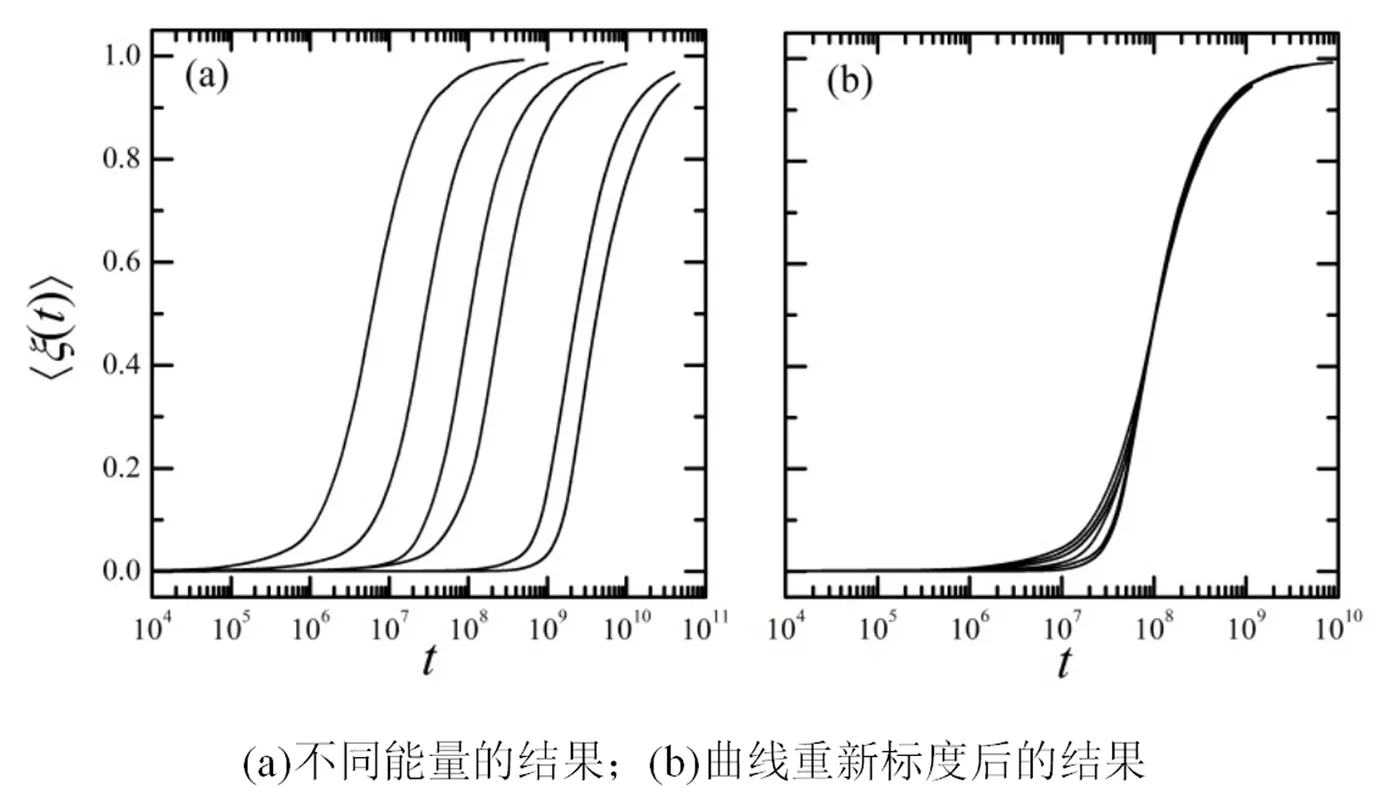
图5 δ=0.5时,取不同的能量E时ξ(t)随时间的变化
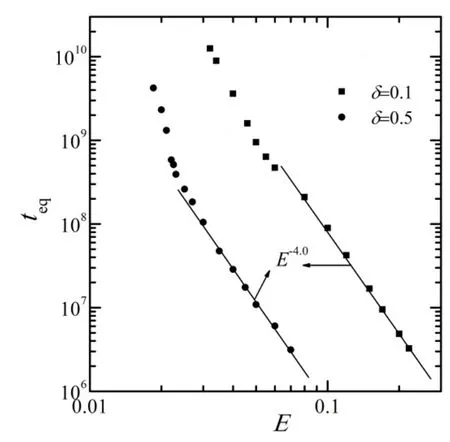
图6 δ取不同值时热化时间teq与系统能量E之间的关系
3 结论
(1)周期调制相互作用会加速系统的热化进程。通过对频谱的分析,发现这是由于周期相互作用增加了与基频模发生共振的本征模的数量,从而加快了热化进程。与基频模的共振也造成了这些模上的能量传递要比其他模的快。加大周期调制的强度,热化的进程会进一步加快。这是由于加大周期作用的强度,会造成相邻本征模的频率接近,使得共振更加容易发生。
(2)在一定的能量范围内,teq与E满足teq~E-4.0的标度关系。说明在周期调制的FPUT系统中,非平庸的六波共振依然存在。但是,随着能量的进一步减小,该标度关系不再成立。
(3)周期调制相互作用会对FPUT链的热化产生重要的影响,这包含着丰富的物理意义,了解相互作用对系统热化的影响对研究更复杂的或是真实的系统的热化非常必要。这个方向还有很多问题是非常值得研究的,比如无序相互作用是否会加快FPUT系统的热化,在其他模型中,如Toda 模型、φ4模型等,通过调制相互作用,会对热化造成怎样的影响。这些问题有待进一步研究。
