基于预约需求的共享停车平台泊位分配方法
2020-07-02张水潮蔡逸飞周竹萍
张水潮,蔡逸飞,黄 锐,周竹萍
(1.宁波工程学院建筑与交通工程学院,浙江宁波315016;2.东南大学交通学院,南京211189;3.南京理工大学自动化学院,南京210094)
0 引 言
停车难是影响城市交通有序运行的一大问题,尤其是城市中心区乱停车所带来的交通秩序问题十分严重.共享停车为解决停车问题提供了一个新思路,利用停车需求时空分布的差异性,将闲置停车资源共享给需求者,使停车资源最大化被利用.
平台回购停车位空闲时段,租用给其他用户的方法是实现共享停车的有效手段.然而实际中存在诸多问题[1]:①从哪些停车场购买,购买多少车位,回购价格,租用价格等如何确定;②收到停车需求后,怎样判断是否接受需求,分配至哪个车位,用户目标停车场没有车位时是否分配至临近停车场等问题;③如何处理用户的违约停放,用户提出延长停放需求时,如何处理延时和普通需求的关系.这些问题涉及供给方,平台及用户三方利益,决定共享停车能否可持续发展.问题①涉及用户停车行为选择的研究,问题②和③涉及车位分配问题.
停车行为的研究:Dell[2]等建立混合Logit 模型,发现收入水平等个体差异是影响停车收费接受程度的重要因素;Simicevic[3]等根据SP 调查建立logistic 回归模型,分析停车收费标准和停车时长限制对出行者停车行为的影响;唐伯明[4]采用BL模型,建立了平日、节假日城市中心区路外公共停车场停车选择行为模型.
现有车位分配问题的研究,通过构建多目标优化模型确定车位分配.Guo 等[5]采用仿真构建停车泊位回购模型,以泊位需求者利益最大为目标,在停车时间约束下获得停车泊位最优使用策略;Shao 等[6]提出二元整数线性规划问题描述共享停车泊位分配问题;张文会[7]建立共享停车泊位利用率最大化和步行距离最小化的双目标泊位分配模型,采用粒子群算法确定需求分配方案.
上述研究把需求作为一个单独的数值,忽视预约需求包含诸多特定属性,如进入时间,停车时长及延时时长.平台实际运作时,需要根据每一时刻停车场的具体占用情况,判断是否存在车位,哪些需求应该被接受,使平台利益最大化.本文从平台角度出发,提出一种基于停车需求的分配方法;以平台收益及用户的步行距离作为目标函数,提出随机可行解的生成方法,使用蒙特卡洛法求解.
1 泊位分配模型
1.1 基本请求下的分配模型
假设如下:
(1)适当步行范围内存在多个停车场,用户需求集中于该范围内.
(2)区域内各停车场根据以往停车占用情况,确定开放时段及可出售车位数.
(3)平台向区域内停车场购买空闲车位.
(4)平台收集预约需求,根据平台收益判断需求分配策略.
(5)停车需求分为基本和延时两种.基本请求时,用户提供驶入时间和停车时长;延时情况,用户提供延长时间.
集合、变量、参数的定义如表1所示.

表1 集合、变量、参数定义Table 1 Definitions of sets,variables and parameters
1.2 模型构建
(1)目标函数1:平台效益最大化.
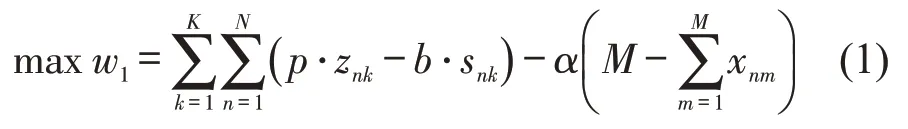
式(1)第1 项是租用车位利润减去回购车位的成本,第2项是停车请求被拒引起的潜在惩罚损失.
约束条件为
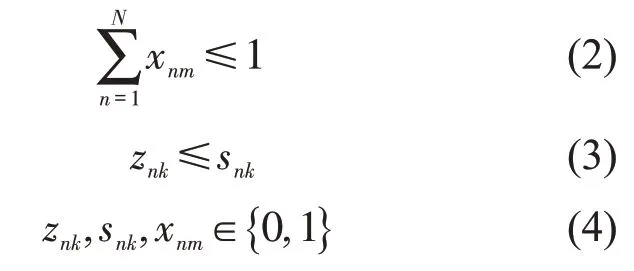
式(2)表示任一请求至多分配一个车位,式(3)表示单个泊位同一时刻至多容纳一辆车.
(2)目标函数2:停车步行距离最短.
用户被分配至非初始目标停车场时,需考虑该停车场与目标停车场的距离.
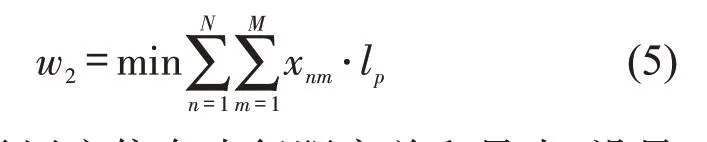
式(5)表示用户停车步行距离总和最小.设最大停车步行距离lmax=350 m.则

采用权重法处理多目标优化问题,最终目标函数为
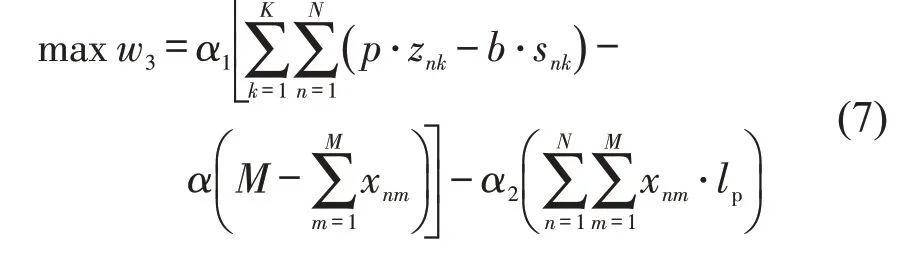
约束条件为式(2)~式(4)及式(6).
1.3 延时情况下模型假设与变量表达
实际应用中会出现用户延长停放时间的情况.假设:用户只能进行1 次延时申请;延时请求至少提前1 h,即申请停车时长结束前1 h.延时情况下集合、参数与变量如表2所示.

表2 延时情况集合、变量、参数定义Table 2 Definitions of sets,variables and parameters under delay situation
1.4 模型构建
延时需求分配前,使用本文构建泊位分配模型进行初始分配,得到平台初始利润w1,以及各泊位占用情况znk.在此基础上,以平台收益最大化为目标,对延时需求进行分配,即
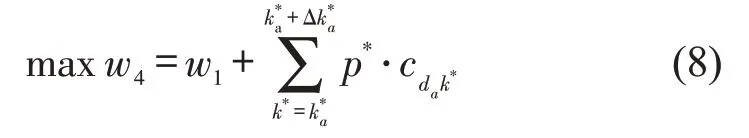
式(8)第2项是延时停车增加的利润.
约束条件为
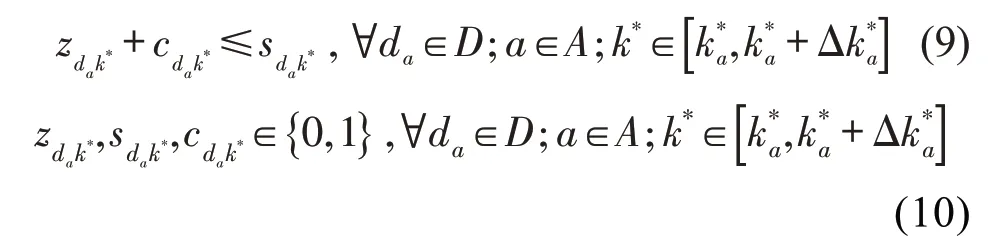
式(9)表示只有当车位da在延时时段全空时,延时请求才可被接受.
2 求解算法
假设平台从区域内部停车场h(h∈H)构买np个停车位,总计在P个停车场购买N个车位.在初始时刻,车位均为空闲状态,区域内共有m个待分配的停车需求,需求解变量为xnm,即确定需求m是否被分配至车位n,为n×m的0-1矩阵.每一列至多有一个1,表示一个需求至多被分配至一个车位中;若该列都为0,表示该需求被拒绝.不同于传统最优问题,该分配问题没有明显的下降梯度,且当前阶段的分配结果受制于上一阶段残留的车辆,故采用蒙特卡洛法计算.
随机生成解集未考虑车位是否被上一时段残余车辆占据,故先确定合理的解集生成条件,以缩小解集范围,使蒙特卡洛法更容易找到最优解.
2.1 生成解集
Step 1k=1 时刻,初始化Xnm矩阵为n×m的0 矩阵,xnm∈Xnm,Znk为n×K的0 矩阵,znk∈Znk.vk为k时刻的空闲车位编号,将矩阵Xnm第mk(表示k时段进入停车场的需求)列的任意空闲车位n设为1,表示时刻1时第mk需求被分配至任意空闲车位n.更新vk,剔除车位n.将k=1 时刻所有需求随机分配至车位,会出现两种情况:
情况1k=1 时刻仍有空位,且没有车辆被分配至同一车位.
情况2k=1 时车位已满,且有需求被分配至同一车位.
当需求大于供给时任意分配车位,无法判断哪些需求应该被拒绝,先将所有需求随机分配至一个车位,可能出现情况2.
Step 2若出现情况1,进入Step 3;若出现情况2,寻找k时刻Xnm同一空位出现多个需求的情况,更新Xnm使k时刻的任意空位至多容纳一个需求,进入Step 3.
Step 3根据k时刻的Xnm矩阵,读取需求mk的停车时长,更新Znk矩阵,计算k+1 时刻的空闲车位编号,更新vk+1,进入Step 4.
Step 4设k=k+1,将矩阵Xnm第mk列的任意空闲车位n设为1,更新vk,剔除车位n.同样出现Step 1中两种情况,进入Step 2.
Step 5若k=K,结束算法,生成随机解Xnm.
此时的Xnm为将k时刻的需求随机分配至任意空位的结果,且不存在同一时刻任一空闲车位被分配两个以上需求的情况.
2.2 确定分配结果
随机解生成后,蒙特卡洛法进行L次循环.随机解集已涵盖式(2)~式(4)和式(6),只需带入式(7),找出目标函数最优的解集即可.延时情况与非延时情况大致相同,不同在于Step 3 设置Znk矩阵变量时,要根据每一时刻的延时需求修正Znk的取值.
3 实 验
以宁波妇女儿童医院停车场为共享停车目标对象,现阶段难以收集平台预约停车信息,故以周边3 个不同用地性质(酒店、住宅、办公)的停车场作为需求来源,医院作为泊位供给方为其余3个地块的过量停车需求提供泊位.
3.1 停车共享条件判定
(1)泊位占用特性.
整理医院1 星期内的泊位变化数据,如图1所示.
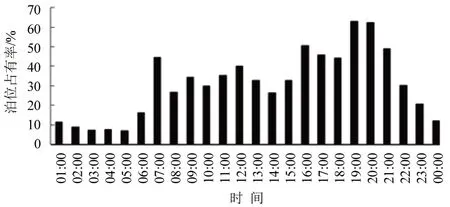
图1 日均泊位占用率变化Fig.1 Average daily occupation rate
由图1 可知:①白天停车高峰集中在07:00 与16:00;夜间停车高峰集中在19:00.②13:00 停车需求减少,出现低谷;21:00 之后停车需求急剧减少,[22:00,06:00]停车需求一直处于较低水平.
(2)车辆驶入/驶离特性.
图2为日均车辆净增长量变化.
由图2可知:①车辆驶入高峰期为06:00、19:00.②车辆驶离有3个高峰期,即[11:00,13:00],[17:00,18:00],[21:00,22:00].③夜间22:00开始,驶出量降低,[00:00,06:00]驶离车辆数较少,几乎不存在车辆驶入.夜间车辆驶入/驶离特征与泊位占有率在低水平相符合.
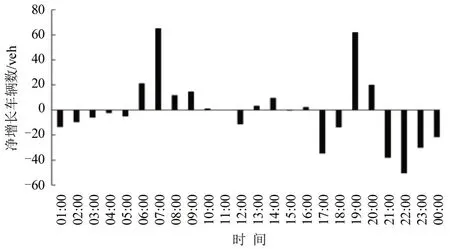
图2 日均车辆净增长量变化Fig.2 Average daily net increase of vehicles
(3)停放时长特性.
车辆停放时长概率分布如图3所示.大部分车辆停放时长在1.5 h以内,超过4 h极少.
综上,将[11:00,13:00],[17:00, 18:00]作为短时泊位共享时段,[22:00,07:00]作为长时泊位共享时段.
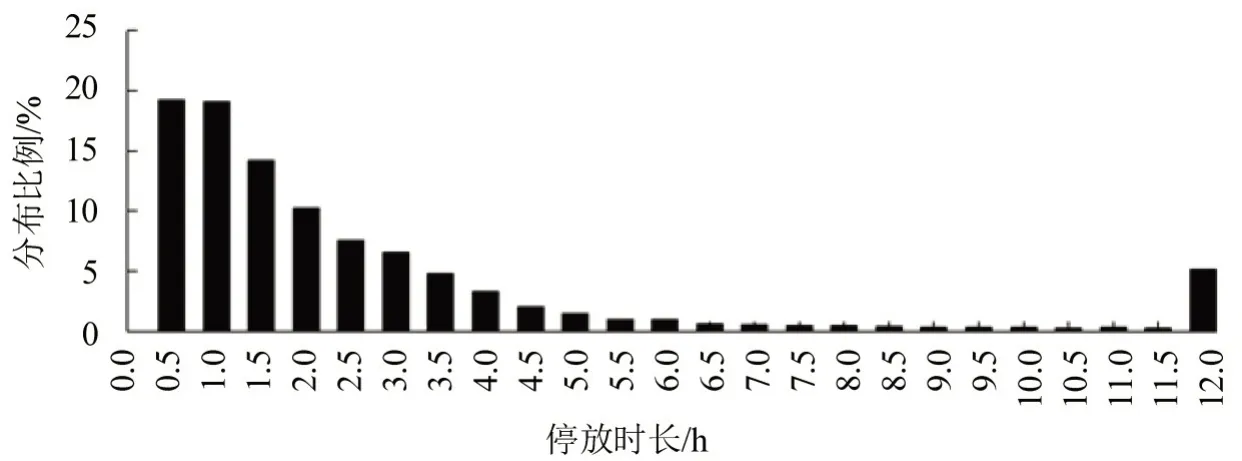
图3 停放时长概率分布Fig.3 Distribution of parking time
3.2 共享泊位分配计算
假设酒店、住宅、办公楼泊位已满,到3个目的地的车辆均通过共享停车平台分配至医院.各时段的共享泊位,各目的地在共享开放窗口的停车需求如表3所示.
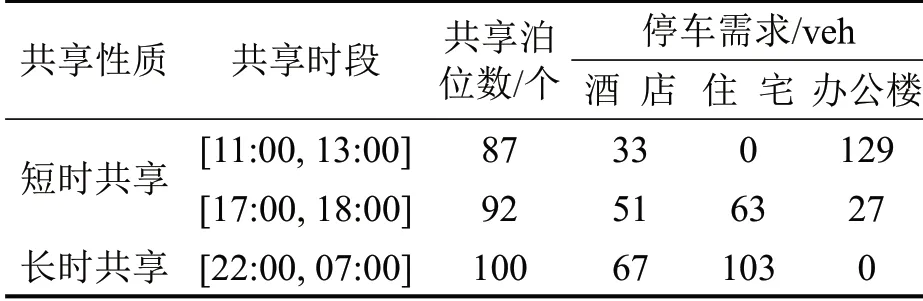
表3 各时段共享泊位供给及停车需求Table 3 Parking berth supply and demand under different time periods
短时共享时间太短,故以长时共享为例.变量取值为:时段为1 h,p=6 元/h,b=2.5 元/h;惩罚因子α=0.5,权重α1=0.8,α2=0.2 ;酒店距离医院348 m,住宅区距离医院300 m;各需求驶入时间服从负指数分布,停车时长服从标准正态分布,需求总时长为898 h,如图4 所示;延时模型中,延时需求为停车总需求的10%,平均延时2 h;用户至少提前1 h提交延时请求,且延时停放结束时间不能超过共享时间窗口.
Guo[5]的研究中,采用3 000次循环确保蒙特卡洛法得到最优解.为确保准确性,本文分别对非延时及延时进行了10 000、20 000 及30 000 次实验.对各次实验得到的目标值从小到大排序,结果如图5所示.
不同实验次数下平台效益最大值一致,说明10 000次实验已能得到最优值.效益值呈阶梯状上升,模型目标是在需求已知的情况下,寻找最优的车位和需求的配对组合,使停车场容纳尽可能多的停车时长.因此,当一种新组合能多容纳一个时长时,效益值会上升,将随机解效益值排序后,形成阶梯状的形式.
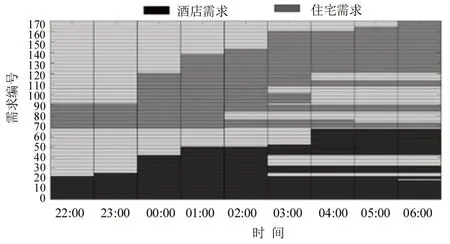
图4 酒店及住宅停车场的初始停车需求分布Fig.4 Distribution of parking demands when first destination are hotel and residence
延时情况的最低效益值为2 954.3,最优值为3 313.2,总收益提升12.15%;非延时情况的最低值为2 721.4,最优值为3 248.7,提升19.37%.总计有898个车时需求,医院100个车位9 h最多提供900车时的停车供给,使部分需求被拒绝.非延时和延时情况如图6和图7所示.观察到00:00以后无论延时还是非延时情况,停车场已基本无空位,需要判断接受哪些常规需求和延时需求,并判断最优组合.
非延时情况占用车时778 h,26 个总计120 个车时的停车需求被拒绝;延时情况占用车时761 h,30个总计154个车时的停车需求被拒绝,没有延时请求被拒绝.没有延时请求时,占用的车时高于有延时请求,这是由于延时请求收费远高于基本请求,最优解会优先满足延时请求,然后考虑非延时请求,使拒绝的基本停车需求高于非延时情况,造成一定的车位浪费,但这更符合平台的趋利性.
4 结 论
本文以共享停车平台收益及用户从停车场至目的地步行距离为优化目标,构建预约请求下,共享停车平台的泊位分配模型.平台从自身利益及保证用户需求两个角度出发,确定最优需求分配策略.运用缩小解集的蒙特卡洛算法,以医院停车场为案例,验证模型及算法在得到最优解时的准确性.针对现状共享停车分配研究的不足,根据停车请求特性,综合考虑停车请求的进入时刻,停放时长,以及延时请求的情况,提出基于蒙特卡洛法的车位分配方法,帮助停车平台确定最优的车位 分配策略,为共享停车的发展提供一定技术支持.
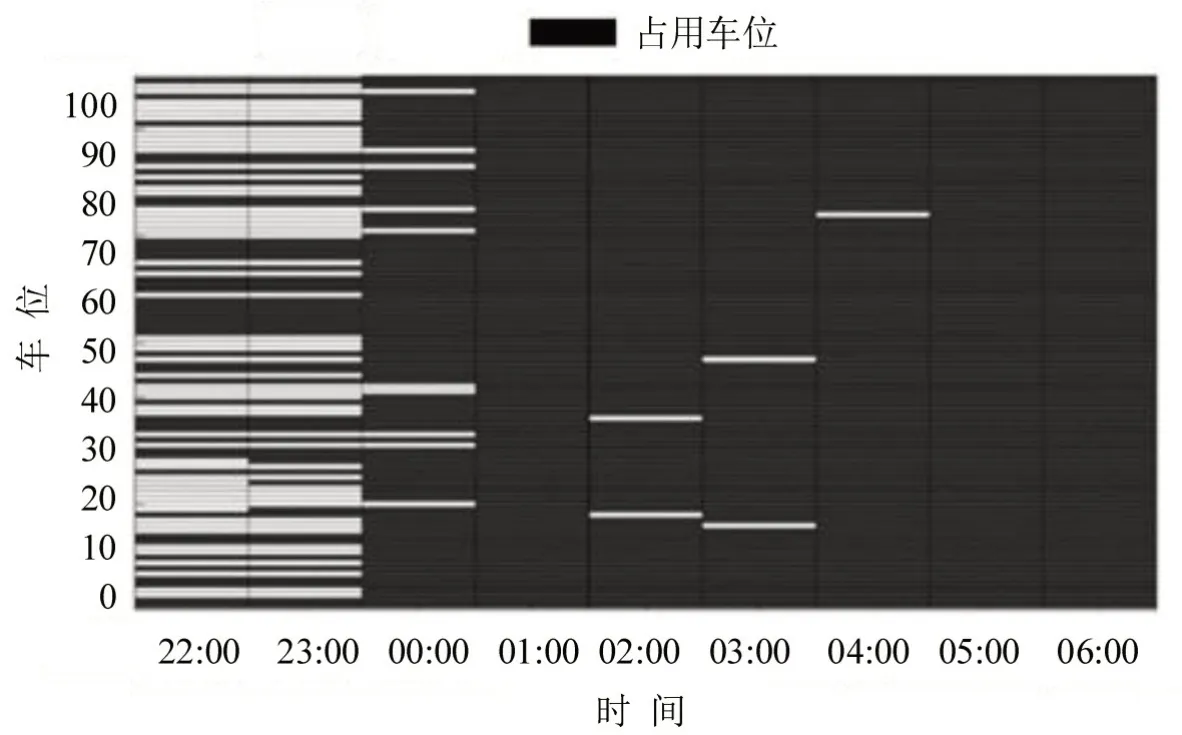
图6 非延时情况的车位占据情况Fig.6 Berth occupation of no delay situation
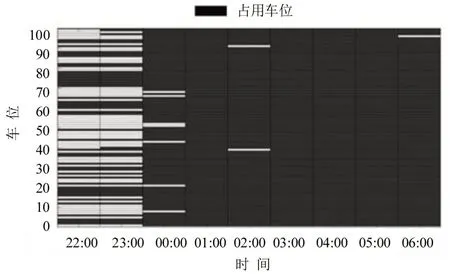
图7 延时情况的车位占据情况Fig.7 Berth occupation of delay situation
本文收集一定时间段内的所有需求并进行分配,需求必须在该时间段之前全部提交,且无法更改,限制了用户选择;另外,未考虑价格因素对共享停车需求的刺激作用.在未来研究中,期望构建以价格为上层变量,用户对价格的反应为下层变量的动态请求分配模型.
