水合物开采对深水锚板基础承载性能影响的THMC 数值模拟研究

黄翔 ，刘芳 *，巨鑫

1 同济大学土木工程防灾国家重点实验室，上海 200092

2 同济大学岩土及地下工程教育部重点实验室，上海 200092

0 引言

天然气水合物是由天然气(主要是甲烷)分子与水分子在特定温度和压力条件下形成的一种笼形冰状晶体。据估计，全球天然气水合物储量是煤炭、石油、常规天然气资源总碳量的2 倍[1]，被认为是未来绿色替代能源。中国天然气水合物总资源量可达8.4×1013m3，主要分布在南海海域、青藏高原冻土区、东海海域及东北冻土区域，其总量约占我国天然气水合物总资源量的77.7%[2]。因此，天然气水合物的资源利用对我国具有非常重大的战略意义。

天然气水合物的开采利用带来了一系列工程问题和挑战。天然气水合物广泛赋存于水深为300～4000 m的海底大陆架[1]，垂直分布深度从海床表面到海床以下几百米。在日益增长的能源需求和科技进步的驱动下，海洋资源的开发和利用逐渐进入深水，浮式深水基础设施(如浮船式生产储油卸油系统、半潜式生产或系泊系统、张力腿海洋平台和立柱式海洋平台等)[4]将广泛分布，其基础结构可能穿越水合物富集区。水合物开采将导致其赋存土体力学性质显著劣化[5]，储层应力状态改变，进而影响深水基础结构的承载性能，给深水基础设施的安全带来隐患。但是这方面的研究目前还鲜有报道。

本文以浮式海洋平台常用的锚板基础为例，采用数值模拟方法研究水合物开采过程对临近深水基础抗拔承载性能的影响。含水合物沉积物是多组分多相多孔介质复杂系统，水合物的开采过程涉及物质变化、热量传递、质量交换和介质变形，伴随热场、流场、力场和化学场的耦合变化。针对水合物开采的热—流—力—化学(Thermo-Hydro-Mechanic-Chemical,THMC)耦合数值模拟研究技术仍然存在诸多挑战。全耦合方法在降低计算成本、解决收敛困难方面尚待突破；将热—流—化学(THC)分析与力学分析进行解耦的时序耦合模拟仍然是主流方法，主要采用非等温多相流分析程序与已有力学分析的开源或商业程序进行耦合，用于分析水合物开采的工程力学效应，如水合物开采过程的海床变形[6]和井壁稳定性[7]等。本文借鉴了上述研究思路，基于美国劳伦斯—伯克利国家实验室开发的TOUGH + HYDRATE多相流分析程序[8]和大型有限元分析商业程序ABAQUS[11]，实现了水合物开采过程中水合物储层—深水锚板基础相互作用的THMC时序耦合数值模拟。

1 数值模型

1.1 单向时序耦合的模拟框架

图1 所示为本文THMC时序耦合的基本框架。首先进行时间离散，在每个时步内THC耦合分析和力学分析分步依次进行，分别由TOUGH+HYDRATE和ABAQUS完成，前者忽略土骨架变形的影响，因此属于单向时序耦合方法。TOUGH+HYDRATE是针对水合物开采所开发的热流分析程序，基于质量与能量守恒方程求解水合物分解过程中的相态演变、质量变化、热量交换和流场变化，可以考虑水合物生成和分解的平衡和动态模型[8]，该程序已被广泛用于天然气水合物的开采模拟[9-10]。

在THC耦合分析中，含水合物沉积物系统的多物理场耦合基本控制方程组(即质量守恒方程和能量守恒方程)可写成统一积分,形式如下 ：

当上式为质量守恒方程时，κ表示物质，即甲烷(m)或水(w)；当上式为能量守恒方程时，κ表示热量。Mκ，Fκ和qκ分别表示质量(或热量)增量、液体通量(或热通量)和质量(或热量)的源或汇。Ω为单位方向向量为n的闭合面积Г所围成的任意体积。求解式(1)可以得到孔压场演变过程以及水合物分解锋面扩展。

如图1 所示，每个时步内，THC分析所得到的孔压和水合物饱和度的空间分布传递给力学分析模块，根据当前水合物饱和度值更新水合物赋存土体的力学参数(如弹性模量E、黏聚强度c和内摩擦角φ)。由于温度变化范围小，相较于渗流场和化学场而言，温度场对力场的影响较小，在此未予考虑。

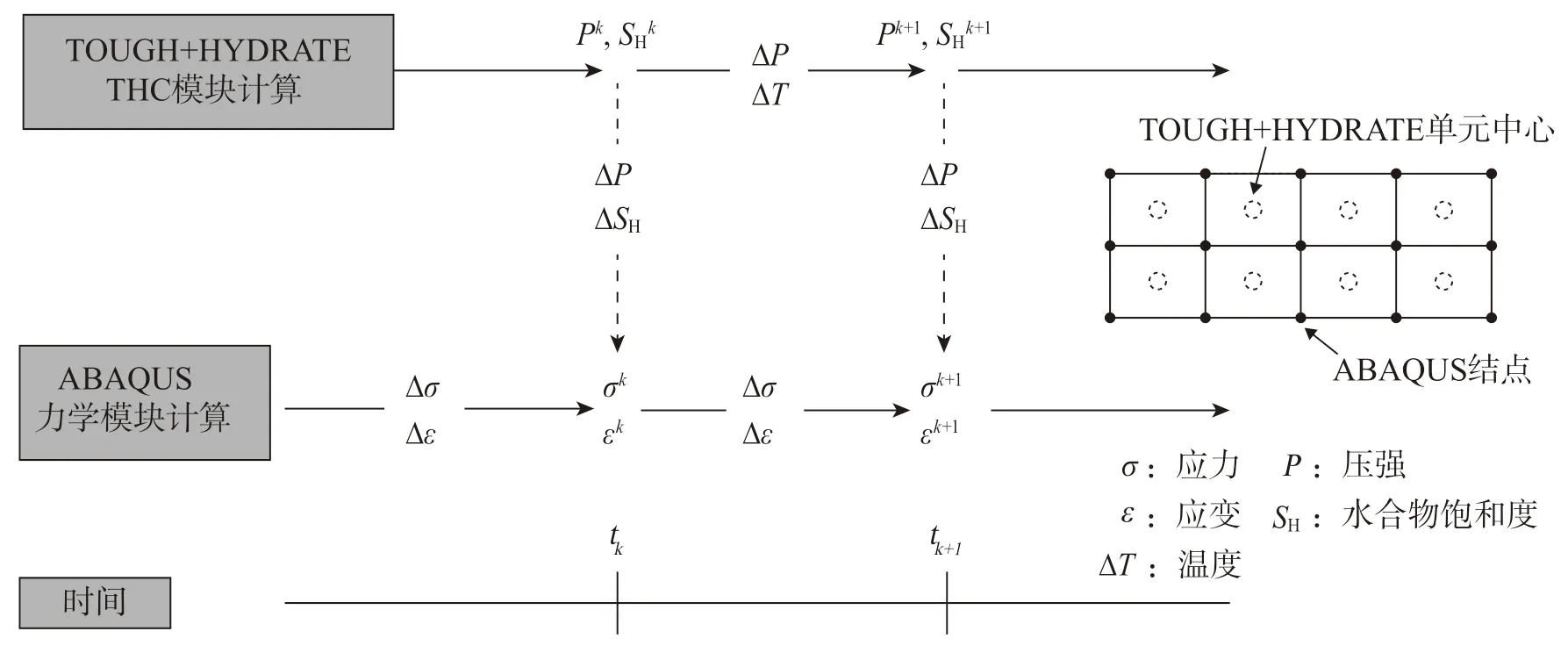
图1 THMC单向时序耦合示意图Fig. 1 Illustration of THMC one-way sequenced coupled process

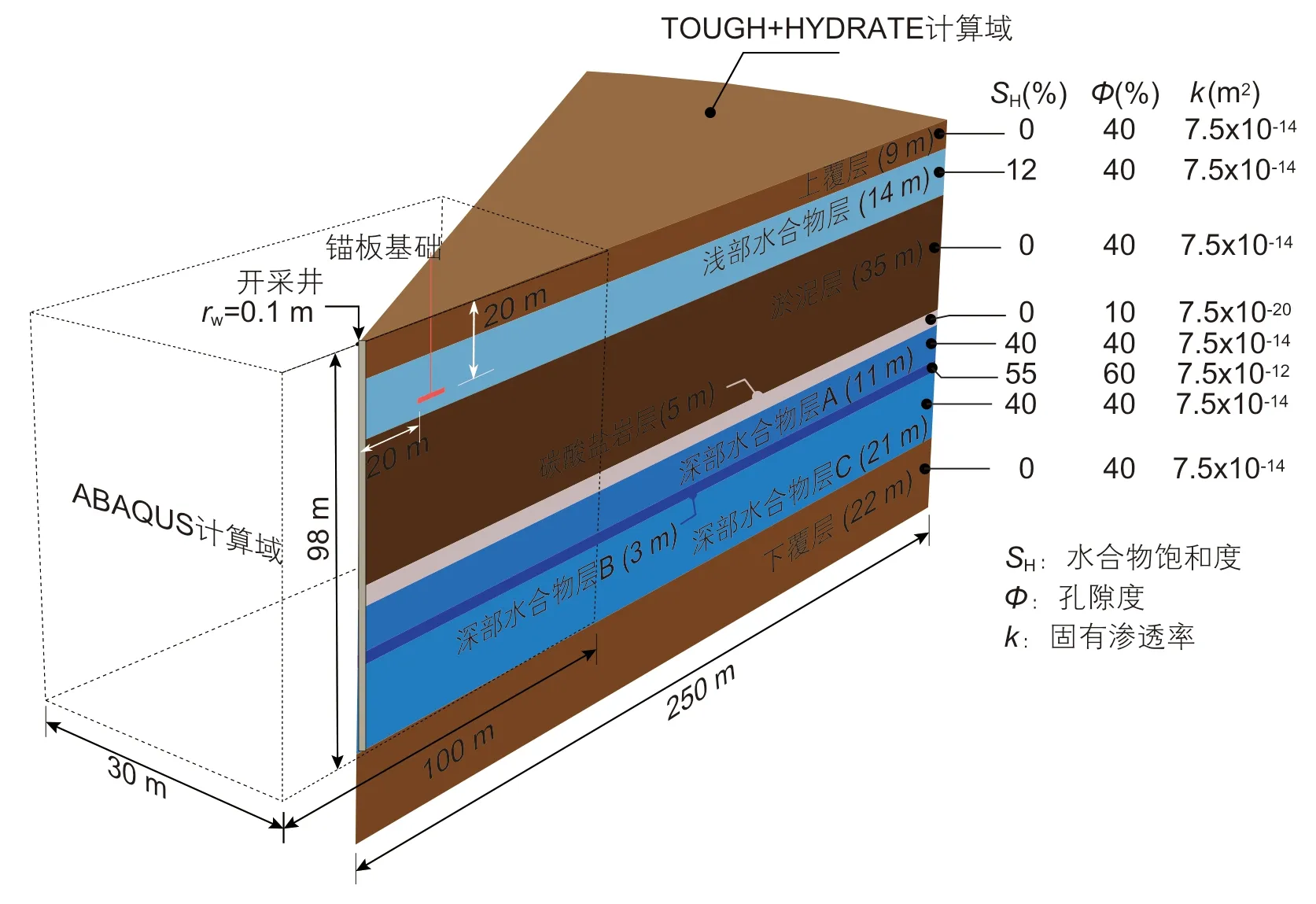
图2 模型示意图和储层参数Fig. 2 Schematic illustration of the model and reservoir parameters

1.2 数值建模

1.2.1 THC分析模型

本文模拟中国南海东沙某区域的竖井降压开采水合物的过程及其对临近锚板基础承载性能的影响，场地条件参考2013 年GMGS2 调查航次8 号钻井数据，开采条件和模型参数参考文献[13]。图2 为计算模型的示意图。该场地的水深为800 m，海床温度为4 ℃，地温梯度为0.045 ℃/m，含两个水合物储层，分别位于海床以下9 m和63 m，厚度分别为14 m和35 m，浅部储层的水合物饱和度为12%，深部储层含厚度为3 m的高饱和度夹层(水合物饱和度55%)，该储层除夹层外的水合物饱和度为40%。该场地各土层的参数见表1。

如图3 所示，为了提高计算效率，THC分析和力学分析的计算域有所不同。其中，THC分析部分采用了以开采竖井为轴的二维轴对称模型，计算域的半径为250 m，高120 m，顶部和底部各设置厚0.1 m的隔水隔热层作为边界。开采井半径为0.1 m，深98 m，采用降压开采，压强由静水压力(在8.00～8.98 MPa范围)降为4.5 MPa。

假设开采井内的流体运动也满足达西流，开采井单元的孔隙度设为1，穿越储层部分的完井段不设套管，渗透系数取 5.0×10-6m2，其余部分井筒设套管，渗透系数取1.0×10-18m2[14]。THC的计算网格划分见图3，对水合物层及靠近开采井区域进行了加密。

表1 THC分析的模型参数表Table 1 Parameters used in the THC coupled analysis

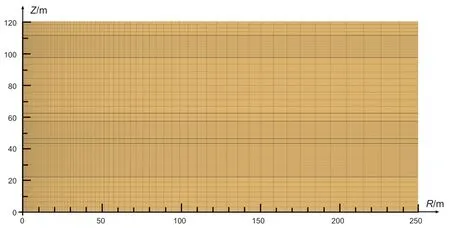
图3 THC模型网格划分Fig. 3 Domain discretization of THC model

1.2.2 力学分析模型

图2 虚线所示为力学分析的三维计算域，长100 m、宽30 m、高98 m，底部边界固定，侧面边界只允许竖向位移。计算网格见图4，采用四结点线性四面体单元，锚板基础附近进行网格局部加密以提高计算精度。

方形锚板基础宽3 m、厚0.3 m、埋深20 m，利用对称性，取1/2 锚板，对称面置于计算域侧面，考虑锚板与开采井距离分别为20 m和40 m两种工况。锚板采用弹性模型，杨氏模量200 GPa，泊松比0.3。为了避免非线性接触带来的收敛困难，将锚板基础与土体的接触模式设置为绑定约束，即假设两者不发生相对运动。

地层的力学参数参考文献[7]，土体采用摩尔—库伦弹塑性模型[18]，按照水合物饱和度值分为4 类土体，主要参数汇总见表2。根据室内水合物土体三轴压缩试验结果[19-21]，随着水合物饱和度的变化，内摩擦角变化不明显。鉴于锚板承载力的大小主要取决于土体的强度参数(即内摩擦角和黏聚强度)，且剪胀角和泊松比变化规律的试验数据欠缺，本文采用了相同的泊松比和剪胀角，并假设土骨架大体相似，选用相同内摩擦角，但考虑了水合物分解所引起的黏聚强度和弹性模量的降低。

在水合物开采过程中，分解锋面持续由井周向外运移，分解区域逐渐扩展，在分解区域内的土体强度和变形参数发生变化。由于分解锋面处的水合物饱和度变化梯度较大，分解锋面范围较窄，为简化计算，忽略分解锋面处饱和度变化影响，预设水合物饱和度阈值(6%)，将水合物储层分为水合物分解区和未分解区，并分别采用相应的材料参数。

力学分析包括9 个分析步，第1 个分析步为地应力平衡，第2 个和第9 个分析步分别为开采前和开采30 年后停采静水压条件下的锚板拉拔试验模拟，第3～8 个分析步分别经历不同开采时间(1 年、2 年、5年、10 年、20 年、30 年)下的锚板拉拔试验模拟。锚板拉拔试验模拟采用位移控制加载，模拟锚板在竖向拉拔情况下的地层变形及破坏情况，得到锚板的力与位移曲线，从而确定锚板在水合物开采过程中的拉拔承载性能的变化规律。

图4 力学分析模型Fig. 4 The model for mechnical analysis

表2 力学参数表Table 2 Mechanical parameters used in the study

1.3 分析模块的交互实现

THC和力学分析模块的数据交互程序采用Python语言编写，将THC分析所得到的孔压场和水合物饱和度计算结果传递给力学分析模型，分析流程见图5。

THC和力学分析的计算网格不同，需将前者结果插值到后者所采用的计算网格中，完成数据交互。即将力学分析模型中的任意节点以开采井为轴旋转并映射到THC分析所采用的二维轴对称平面上，然后在该平面上采用反距离权重插值法[12]，用通过二维轴对称网格单元中心所得到的变量值进行插值，获得待求节点的相应变量值，插值公式如下：

其中，S0为待求点节点坐标，Si为已知点坐标，λi为已知点Si的插值权重，d0i为待求点与已知点之间的距离。

图 5 THC和力学分析模块的交互示意图Fig. 5 Communication between the THC and mechanical analysis

图6 THC分析结果：(a) 产气率；(b) 累积产气量Fig. 6 Results of the THC analysis: (a) the gas production rate ; (b) the cumulative volume of produced gas

2 结果分析

2.1 THC模拟结果

2.1.1 产气速率及累积产气量

图6 为产气率和累积产气量与时间的关系，与文献[13]的分析结果大致吻合。如图6 所示，水合物开采初期的产气率较高，开采2 个月左右达到最高产气率，约7400 STm3/d，之后产气率迅速降低，开采7 年后降至4500 STm3/d左右，随后产气率趋于平稳，开采15 年后产气率逐渐降低，开采30 年后产气率降至3800 STm3/d左右。而产气量持续上升，30 年的总产气量约为5.5×107STm3。

2.1.2 水合物分解锋面扩展

图7 为水合物开采中孔隙压力分布情况，图中虚线框为力学分析域范围。最大降压区位于开采井附近，随着时间推移，由于水合物分解，储层表观渗透率有所增加，下储层井周降压梯度逐渐增加。

图8 为水合物开采中水合物饱和度分布的变化。随着开采进行，水合物分解锋面逐渐向远处延伸。由于温度较高的海水沿压强梯度从下方汇入，加速了下储层水合物的分解，下储层分解锋面的扩展速度明显快于上储层。

2.2 力学模拟结果

以开采10 年后的锚板基础拉拔数值模拟实验为例，当锚板竖向位移分别为0.3 m、0.6 m、0.9 m时的竖向有效应力分布情况见图9。锚板基础承受拉拔荷载时，锚板上方的土体受压，有效应力增大，而锚板下方土体受拉，有效应力较小。锚板对周围土体的影响范围有限，土体的受压区随着锚板基础竖向位移的增大而增大。

图10 给出了不同井距和开采时间下锚板基础拉拔荷载—位移曲线，荷载均随着位移增加而增加。考虑锚板基础抗拔承载性能的充分发挥，选取位移为30%锚板宽度的拉拔荷载作为锚板基础的极限抗拔承载力(如图10 中的虚线所示)。不同井距情况下极限抗拔承载力随着开采过程的变化见图11。

如图11 所示，在水合物开采初期，当井距为20 m时，锚板的抗拔承载力明显提高，因为降压开采导致井周土体有效围压增加，土体摩擦强度有所提高，进而提高了锚板基础的抗拔承载力。当井距为40 m时，由于锚板基础距离开采井较远，降压区影响范围有限，锚板周围土体强度尚未受到降压开采的影响，因此锚板抗拔承载力基本不变。

开采10 年后，不同井距下的锚板抗拔承载力均有所降低，锚板周围的储层由于水合物逐渐分解，导致储层土体黏聚强度持续降低，引起承载力下降。开采20 年后，距井20 m处的锚板周围储层的水合物已全部分解，且土体应力基本稳定，因此锚板基础的抗拔承载力基本不变；但距井40 m处储层水合物还在持续分解，因此该处锚板基础的承载力继续下降。

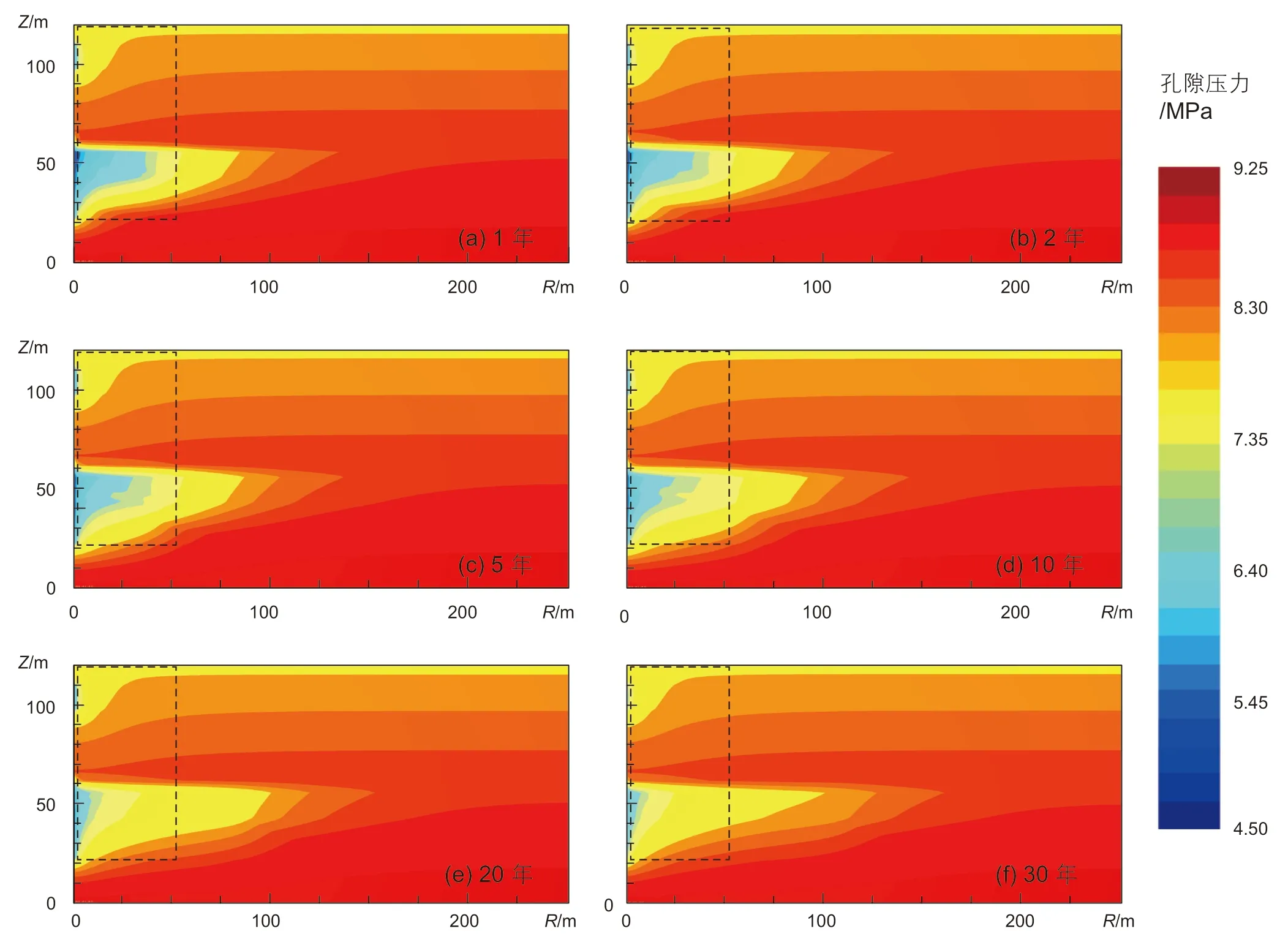
图7 水合物开采过程中孔隙压力分布演化关系图Fig. 7 Evolution of spatial distribution of pore pressure during gas production

图8 水合物开采过程中水合物饱和度分布演化关系图Fig. 8 Temporospatial distribution of hydrate saturation during gas production

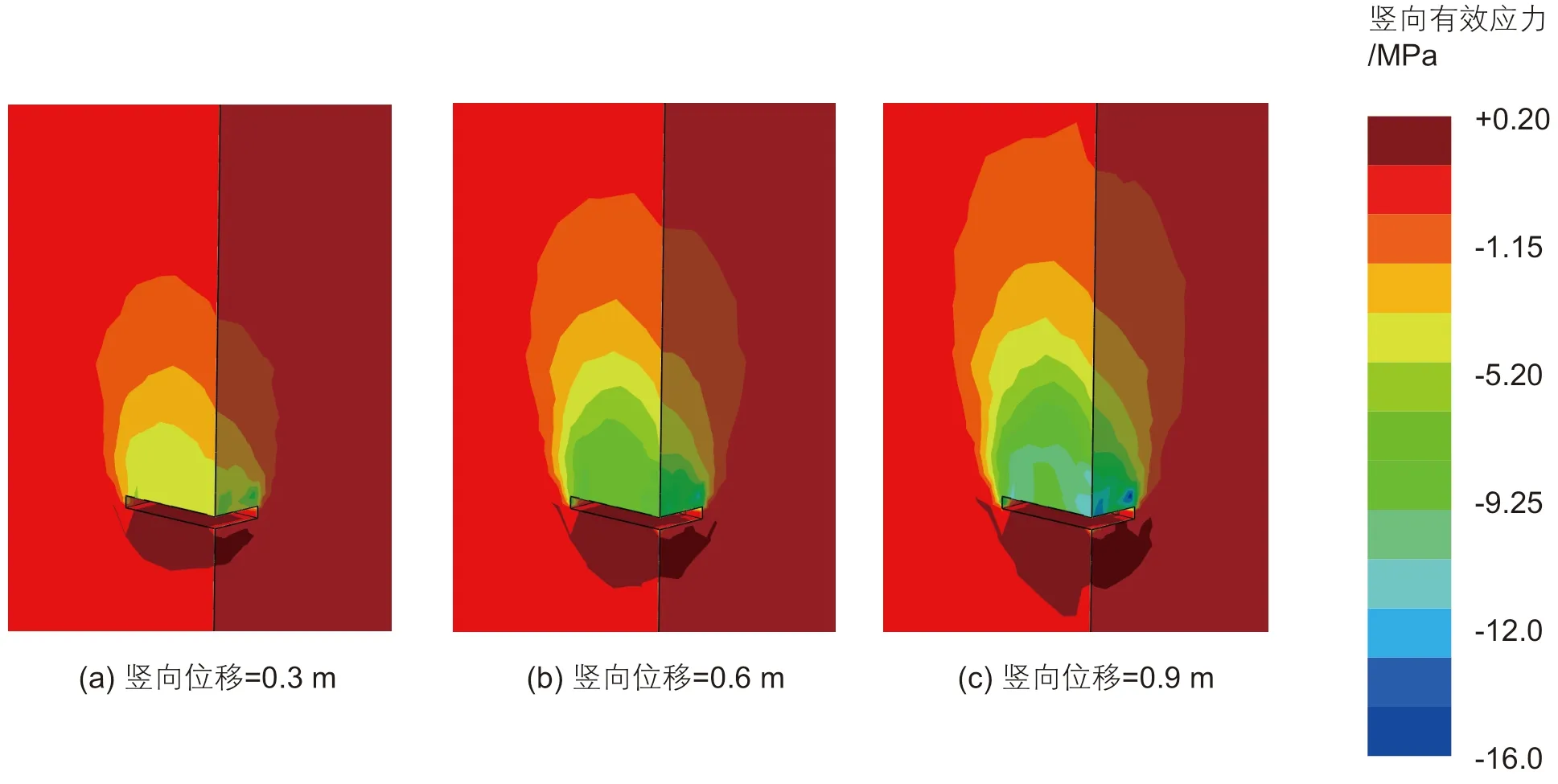
图9 开采10 年后的土体竖向有效应力分布图Fig. 9 Spatial distributions of the vertical effective stress at 10 years

停止开采后，水合物开采所产生的超静孔压逐渐消散，土体中的孔压恢复至初始静水压状态，由于孔压回升导致土体中有效围压降低，土体摩擦强度降低，因此不同井距的锚板基础承载力均明显降低。经过长期开采后停采，不同井距处储层的水合物均完全分解，储层黏聚强度和应力水平都大致相当，因此停采后不同井距锚板基础承载力降至相同水平，且低于水合物开采前的承载力值。拔承载力变化同时受控于两种机制：(1)降压引起土体有效围压增加导致承载力提高；(2)水合物分解引起土体黏聚强度降低导致承载力下降。当锚板距离开采井较近时，第一种机制在开采初期占主导作用，因此锚板承载力有所提高；随着水合物分解锋面随时间扩展，第二种机制的影响逐渐显现，锚板承载力降低。当锚板距离开采井较远时，第二种机制占主导。当水合物停止开采后，孔压对承载力的影响机制逐渐消失，由于不可逆的储层黏聚强度丧失，锚板基础的承载力明显低于开采前初始承载力。

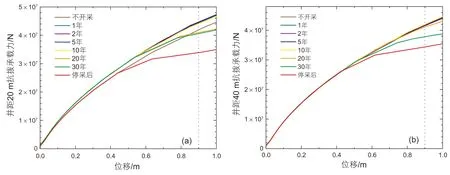
图10 不同开采时间下锚板基础的荷载-位移曲线：(a) 距井20 m；(b) 距井40 mFig. 10 Load-displacement curves of the plate anchor at different times when the anchor is at (a) 20 m and (b) 40 m away from the well

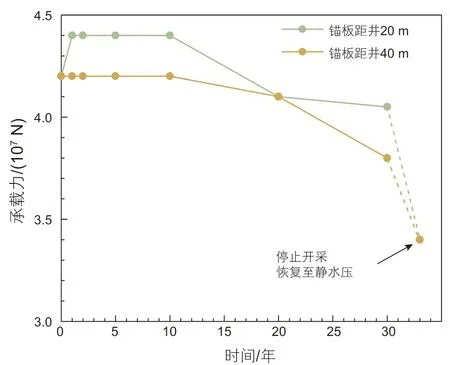
图11 不同井距下极限抗拔承载力随开采时间的变化Fig. 11 The evolving ultimate uplift capacity of the anchor under different well-anchor distances

3 结论

本文开发了含水合物多孔介质的多相流分析程序TOUGH+HYDRATE和有限元商业软件ABAQUS的交互模块，实现了水合物开采过程中储层海床与锚板基础相互作用的THMC单向时序耦合分析，根据南海水合物富集区的典型地层条件建立了储层—锚板相互作用数值分析模型，研究了降压竖井开采水合物过程中锚板基础抗拔承载性能的变化规律，为深海水合物富集区的油气开采和基础设施平台的深水基础设计提供了理论参考。本文的主要结论如下：

(1)降压法开采水合物过程中，锚板基础的抗拔承载力的变化受控于两种不同机制，一是孔压下降引起储层摩擦强度增加从而提高锚板抗拔承载力，二是水合物分解引起储层黏聚强度减小从而降低锚板抗拔承载力。

(2)当锚板基础距离开采井较近时，上述两种机制交替起主导作用，因此抗拔承载力随着开采时间的推移先明显提高随后逐渐降低。

(3)当锚板基础距离开采井较远时，降压的影响机制并不明显，因此锚板抗拔承载力在开采初期大致保持稳定，长期开采之后明显降低。

(4)当水合物长期开采后停采，降压对锚板抗拔性能的影响机制逐渐消失，但由于水合物分解导致锚板基础周围储层土体的黏聚强度已丧失，与开采前初始抗拔承载性能相比，停采后的锚板基础抗拔承载力降低至20%左右。