既见树木，又见森林

高小娣，高级教师，江苏省海安市城南实验小学副校长，江苏省南通市学科带头人，《教师博览》签约作者。先后在全国及省、市教学竞赛中获一等奖，在《江西教育》等省级以上期刊发表文章40多篇，参加“一师一优课，一课一名师”活动获评部级“优课”。先后应邀到河南、浙江、甘肃等地上示范课或做讲座。

导 读：

数学是一门“结构的科学”。整体性、结构性是数学学科的本质特性。针对小学数学课堂教学中的“去结构化”现象，探索指向整体建构的教学实践，很有必要且很重要。本文从“为什么”“是什么”“怎么办”三个方面，深入阐述了结构化教学的存在意义和实施策略。

数学常常被称为“结构的科学”。结构是什么？瑞士儿童心理学家皮亚杰早在1968年出版的《结构主义》中写道：“所谓结构，也叫一个整体、一个系统、一个集合，是一个心理系统或整体。”数学教学，就是要把“结构”作为一种重要的研究方向。正如《义务教育数学课程标准（2011年版）》研制专家组在解读课程标准时指出的：“我们的课程应当使学生真正感受到数学内容本身所具有的‘整体性——数学是统一的，许多不同内容之间存在着实质上的联系，包括内涵和方法。”从一定意义上来说，指向整体建构的教学实践，既是教学现实的积极回应，也是数学教育的本质回归，更是育人价值的全面凸显。

一、为什么——“去结构化”的现象扫描

（一）知识点状化

数学教材中的知识点通常以散点形态分布在各册教材各个单元中。许多数学知识点之间的关系被隐蔽、被搁置，导致学生的整体认知被肢解、思维方式被固化、创新精神被弱化等现象仍然存在。例如，教学苏教版数学一年级下册“元、角、分”时，“元”“角”“分”都是人民币单位，它们之间的关联就是元与角、角与分、元与分之间的进率。通常教师在课堂板书时，把元、角、分三者之间的进率写成3行，分别是“1元=10角”“1角=10分”“1元=100分”，这样的板书设计，虽然把元、角、分的进率表达清楚了，但知识点之间关联性不强，呈现一种“散点”状态，没有将3个人民币单位连成一个整体。板书时，教师可以将元、角、分写成1行，元与角、角与分之间用双向箭头，上面都标上进率10，下面在元与分之间用双向箭头，在下面标上进率100（如图1）。这样的课堂板书就有了严密的逻辑，整体感强，有视觉冲击力，直观、形象且易记。

图1

（二）板块孤立化

不少教师采用“单课时”备课法，侧重于对课时内容的细节雕琢，忽视对整体背景的宏观把握。这样缺乏知识之间的纵横沟通、内外关联，必然导致知识板块的孤立、知识系统的割裂。例如，“比的基本性质”是化简“比”的依据。如果仅仅围绕“什么是比的基本性质”“比的基本性质有什么用”“怎样运用比的基本性质”3个问题来开展教学，这些知识就显得有些孤立。如果站在全册数学教材的高度来审视这一教学内容，就会发现以前学过的“商不变的规律”和“分数的基本性质”与本课知识存在着十分密切的关联。把这两个知识点融入本课教学，其前后知识的整体性、关联性、结构性就比较完整了。

（三）流程机械化

长期以来，教师都习惯于按照线性结构来组织教学。传统的“五步教学法”（复习铺垫—导入新课—教学例题—巩固练习—课堂小结），是一种时间进程与认知过程相结合的教学结构类型。随着学生获取信息的多元化以及素养为本、能力为重的教育呼声的高涨，传统的课堂教学结构暴露出越来越多的弊端。例如，教学苏教版数学六年级上册“百分数的意义”时，学生在生活中已经接触过有关百分数的知识，按照传统的教学流程，就容易使學生脱离生活实际学数学。如果联系生活中学生已经认识的百分数重新设计教学流程，既有助于学生理解百分数的意义，又有助于学生体验到百分数与生活的密切关联，这样的教学就有了意义取向，关注了知识，更关注了知识背后的意义。

二、是什么——“结构化”教学的内涵诠释

基于以上“去结构化”的教学现象，对小学数学进行“整体建构”教学就显得尤为迫切且必要。通过结构化教学，学生完善认知体系，发展思维能力，培育思维素养，进而更好地理解数学，爱上数学，轻松地学好数学。

（一）整体关联是抓手

数学知识有着很强的内在逻辑，是整体的、系统的、结构的。结构的本质是元素及其关系的整体关联。正如郑毓信教授在《新数学教育哲学》一书中认为：“数学对象的性质就完全反映于它们的相互关系。这也就是指，数学对象的建构事实上是一种整体性的建构。”纵观小学数学全套教材，我们可以看到，数学知识之间有一套严格的逻辑系统，但它们散落在各册教材中。我们力求寻找不同领域、不同年段、各分册知识内容的内在逻辑关联，将数学知识点“拎起来”“串起来”“连起来”，从而连成线，串成块，织成网，构成体系。这样的教学有助于培养学生的结构化思维。

（二）动态建构是核心

知识结构的不断重组或重构是数学思维发展最为重要的一个特征。提出指向整体建构数学教学，不仅因为数学知识本身是结构化的，更因为学生认知、思维也是结构化的。正如皮亚杰所说的：“教学就是让学生认知心理从平衡到失衡再到新平衡的过程。”结构化教学就是一个建构、解构、重构的动态过程。教学中，我们不应拘泥于教材中的层次和脉络，而要努力让数学学习在建构、解构、重构的过程中，促进数学思维的深度发展，实现数学核心素养的关联生长。

（三）发展思维是方向

“数学是思维的体操。”数学学习要引导学生在学习活动中切身体会思维的力量，并最终成为“思维的主人”。因此，促进学生思维的发展是小学数学教学的根本任务，也是重要目标。“为思维而教”是小学数学教学的宗旨，培养数学思维是整体建构小学数学教学的方向。发展学生思维，不能仅仅停留在思维方式方法的简单使用上，而要突出对思维品性、思维品格的培养，迈入高阶思维的发展境界。思维结构化是结构化教学的一个重要目标，甚至是终极目标。这样的结构化教学，才是有生命力的、有意义的。

三、怎么办——“结构化”教学的实施策略

（一）串联——跳出教材看教材

1.统揽全册教材，上好“开学第一课”。新学期“开学第一课”是对学生进行结构化教学的好时机。教师可以引导学生统揽全册教材，从整体上认识本学期数学学习的基本内容，其中哪些内容与以前学过的知识是有联系的，帮助学生形成知识结构，建立数学关联，促进儿童结构化思维的发展。例如，教学苏教版数学六年级下册“开学第一课”时，教师可以和学生聊一聊本册教材目录，让学生圈一圈自己感兴趣的内容;看到“扇形统计图”，教师可以引导学生回忆已经学过哪些统计图;看到“圆柱和圆锥”，教师引导学生猜测这部分内容与以前学过的哪些知识可能有联系。帮助学生树立信心，让学生明白，新学期的数学知识并不难，它就是在已有经验的基础上往前走了一步，都是某个知识板块中的一部分。

2.梳理全套教材，绘好“结构全景图”。数学学习是一个整体的认知过程，小学数学教材内容和数学教学也应该是一个系统的整体。这就要求教师整体把握小学数学全套教材，站在一个较高的层次上用大数学观去审视和处理教材，向学生传递完整的数学思想，帮助学生形成融会贯通的数学认知结构。我们勾勒了苏教版小学数学12册教材的知识结构全景图，力求寻找不同领域、年段、年级及各分册知识内容的内在逻辑关联，将小学数学知识连点成线、织线成网，形成一体化的知识网络。有了“全景图”，在教学实践中教师就能从整体上把握教材结构，合理运用教材，形成结构化的数学教材观。

（二）融合——超越教材教教材

1.纵向到底的领域内融合。小学数学教材分为“数与代数”“图形与几何”“统计与概率”“综合与实践”等领域。所谓“领域内融合”，就是对某个领域内的学习内容、方法等进行拓展、延伸、补充。例如，教学苏教版数学五年级上册“负数的初步认识”时，教材借助数轴来帮助学生理解正数、0、负数，让学生在数轴上填写正数或负数。当练习中出现了正小数、负小数、正分数、负分数时，学生能够判别出正、负数，但不容易比较出它们的大小。教学时教师可以将正、负数纳入原来的已知数系中，并在新的数系中进行建构，生成新的数系结构。

2.横向到边的领域间融合。领域间融合最为普遍，即将某一个领域内容融入另一个领域内容，如“数与代数”领域与“图形与几何”领域的融合，“图形与几何”领域与“统计与概率”领域的融合，甚至表现为3个领域的融合，等等。例如，教学苏教版数学三年级下册“小数的初步认识”时，教师借助正方形图引导学生经历从“1”到创造“0.1”再到认识几个“0.1”的过程，再让学生从“0.1”中创造“0.01”等小数，数形结合，直观形象，简洁明了。教学时，教师还可借助计数器帮助学生建构相邻两个计数单位之间的进率是10的模型。学生创造新单位，生长新数位，在原有计数法则的基础上进行推理、创造，从而完成自我认知的突围，实现小数意义的整体建构。

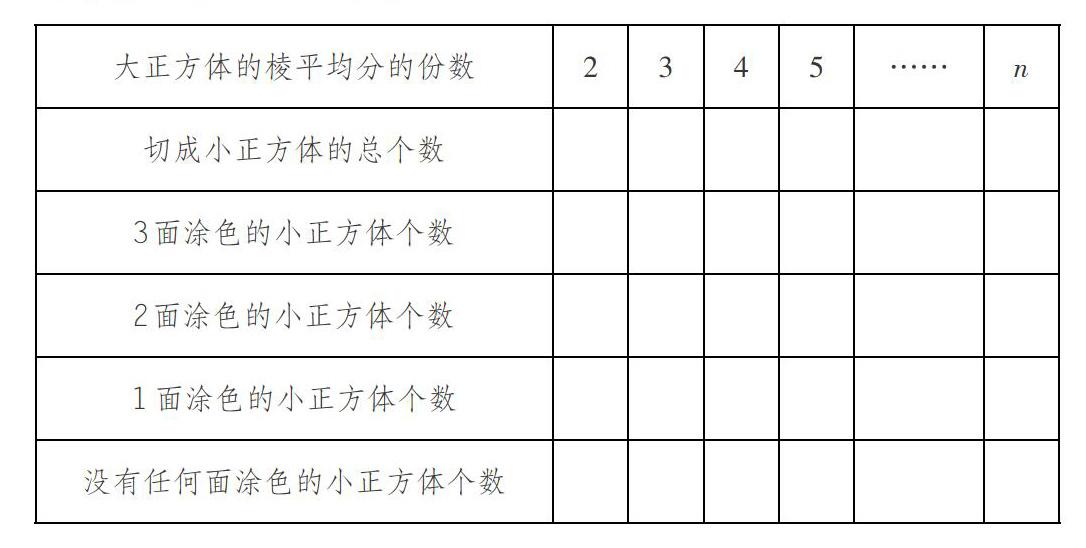
3.纵横交叉的超领域融合。有些知识的教学，既有领域内的融合，又有领域间的融合，我们把它们称之为“超领域融合”。这种融合方式是一种更高级别的大融合。例如，教学苏教版数学六年级上册“表面涂色的正方体”时，教材安排了将大正方体沿着每条棱平均分成2份、3份、4份、5份……然后再切成同样大的小正方体，分别探究“切成小正方体的总个数”“3面涂色的小正方体个数”“2面涂色的小正方体个数”“1面涂色的小正方体个数”。教学中，我们可以进一步拓展，增加探究“没有任何面涂色的小正方体个数”，这是领域内的融合。同时，我们又将原来的表格改为下面的表格：

这样的表格设计，利用数形结合实现了领域间融合。有了充分的探究活动，进而归纳、比较、概括，学生对涂色问题的规律理解更为深刻。在此基础上，教师还可以引导学生探究将一个大长方体切成若干小正方体的规律。比较长方体和正方体涂色的规律，提炼出更为普遍的规律。知识领域内及领域间不断纵向、横向融合，使得学生的认知不断地结构化。

（三）组块——聚焦单元看单元

1.聚焦内容结构，架构单元教学的知识体系。教师要对教学内容进行多元联结，呈现结构化、模块化的知识体系，促使学生从碎片化、浅表化学习走向结构化、深层次学习。例如，教学苏教版五年级下册“分数的意义和性质”时，教师紧扣“分数意义理解”这一核心元素，将其作为主线贯穿整个单元教学;教学“假分数”时，让学生填空[（）4]，当学生说出[54]时，首先让学生判断这个数是不是分数，然后引导学生理解并画图表示[54]的含義;在数轴上表示[（）4]的分数时，重点让学生说一说[44]、[84]、[124]这些特殊分数的含义，体会假分数与整数的联系。这样的内容结构，加深了学生对分数单位概念内涵和外延的理解，帮助学生从整体上架构了分数知识体系。

2.聚焦思维结构，彰显单元教学的核心要义。抓住核心和关键，扣住本质和联系，凸显整体和关联，数学学习就能化繁为简、化难为易。例如，教学苏教版数学二年级上册“表内乘法”时，有这样一道题：“小明左手拿了6支铅笔，右手拿了3支铅笔，一共拿了几支铅笔？”有部分学生选择用乘法来计算，究其原因在于学生刚刚学习乘法，容易形成用乘法解决问题的思维定式。如何避免这一问题呢？教学时，教师可以创设不同的问题情境，打破“学乘法用乘法”的惯性思维，引起思维冲突，让学生迅速调用头脑中已有经验解决问题。不同的问题结构，不同的解决方法，有利于培养学生的结构化思维，发展学生的高阶思维。

（四）变式——立足课时用课时

1.教法变式思路宽。教学中，教师可以通过变式教学来促进学生对数学概念的结构化理解。尤其是在新授环节，对重点知识的理解可以通过多元化途径，帮助学生深刻理解概念内涵，达到结构化理解的目的。例如，教学苏教版数学三年级上册“认识几分之一”，在操作探究环节中，教师给学生每人发放一张同样大小的长方形纸片，让学生折出它的二分之一并涂上颜色，再在小组内交流。交流时，学生依次呈现不同的折法。在此基础上，教师追问：不同的折法，每一份的形状都不一样，为什么都可以用二分之一来表示？还有其他折法吗？这些问题进一步激发了学生的探究热情。在这个教学过程中，不同的折法正好构成了一个有机整体，帮助学生形成较为完善的认知结构，学生对分数概念的理解从肤浅走向深刻。

2.流程变式教法活。结构化教学离不开建立清晰完整的课堂教学结构。在课堂教学实践中，我们尝试以“问题”为主线，在图形面积教学中探索“发现问题—提出问题—分析问题—解决问题—产生新问题”的教学结构;我们以思维为主线，在探索规律教学中建立“发现猜想—验证猜想—归纳概括—反思拓展”的教学结构，等等。例如，教学苏教版数学六年级上册“百分数的意义”时，教师课前布置学生收集生活中的百分数，课始请学生上台交流对这些百分数的认识，然后基于学生的认知基础相机教学。这样的课堂结构变式，让数学课堂拥有张力。

指向整体建构的教学实践，遵从了数学学科整体性、结构性的本质特征，顺应了儿童自主性、能动性的内在需求，彰显了素养至上、育人为本的价值追求。实践表明，在数学教学中倡导结构化学习，能够实现“既见树木，又见森林”的理想状态。当学生的结构化思维自我突破、自主建构、自觉生长时，我们就可以说，学生的数学素养真正形成且不断形成，数学教育的价值也真正得以实现。

（作者单位：江苏省海安市城南实验小学）