基于Dijkstra算法过必经点的最短路径设计
2020-07-01王小会薛延刚李晓青
王小会, 薛延刚, 李晓青
(兰州工业学院 电气工程学院,甘肃 兰州 730000)
随着车辆的广泛普及和交通网络的不断发展,智能交通诱导系统的作用将显得更为突出。智能交通诱导系统是将先进的计算机处理技术、信息技术、数据通信技术及电子自动控制技术等有效地综合运用于整个系统当中,建立起的一种在大范围内、全方位发挥作用的实时、准确、高效的最优出行路线系统[1-6]。
交通诱导系统可根据驾驶员的意愿为其提供最佳行驶路线来达到诱导出行行为,减少车辆在路上的行驶时间[7-8]。对用户来说,除了最优路线外,次优、再次优等路线[9-10]也同样重要,这样可以使用户拥有更大的选择空间。同时,为了进一步提供更人性化的服务,诱导系统还应设置多个必经点以满足用户在出行途中的需要,比如要途径超市、加油站等,故必经点的考虑也必将是未来智能交通诱导系统的发展趋势[11-16]。因此,本文在基本Dijkstra算法上提出过K个必经点的N条最短路径算法,有效扩充了最短路径的数量,满足用户选择需求。
1 交通诱导系统的设计
1.1 系统设计
首先通过建立路网节点属性数据库保存相关节点信息,并将路网信息数据导入到数据库,完善路网结构信息;其次,通过Dijkstra算法查找出符合要求的最短路径;最后在界面上显示相关的路径信息。具体流程如图1所示。
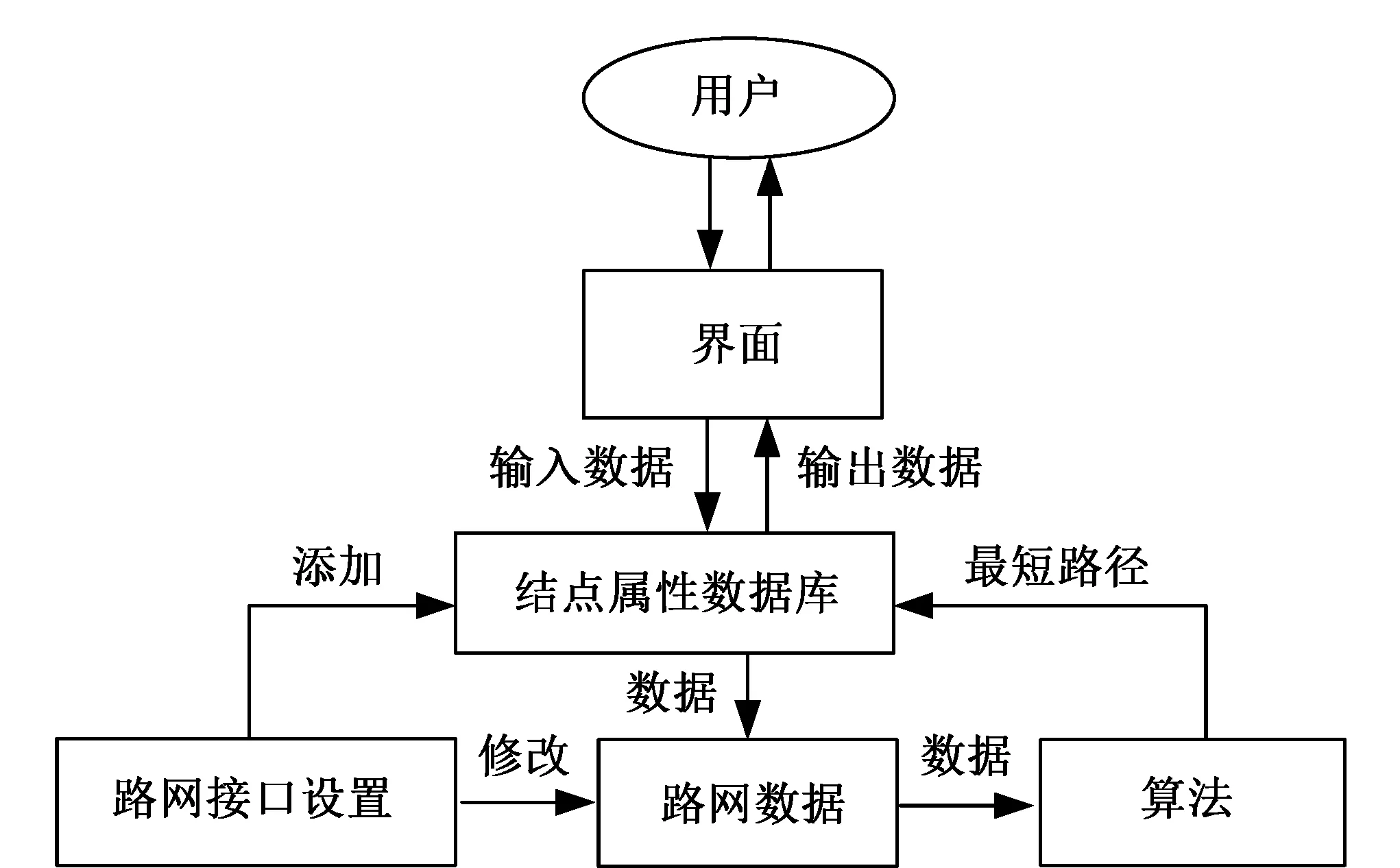
图1 系统设计流程
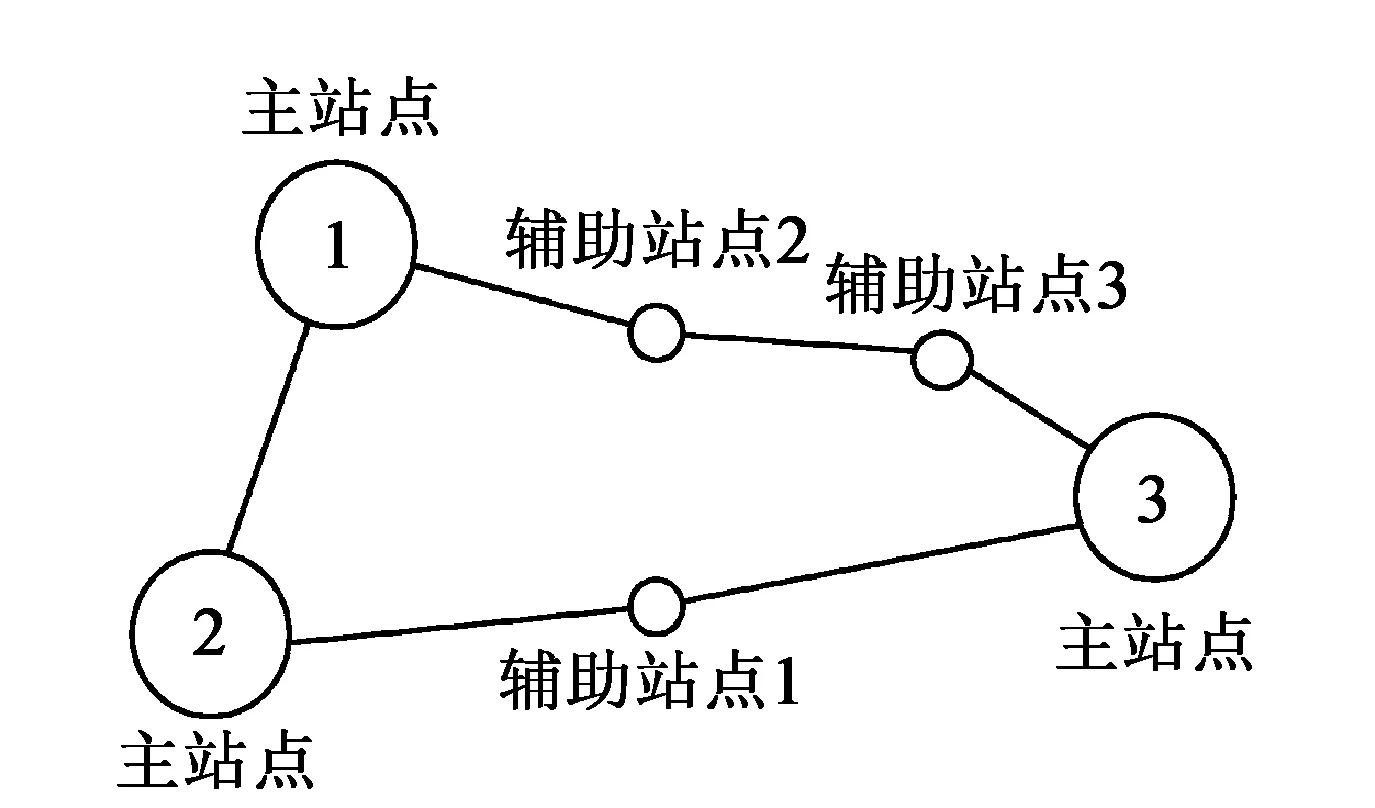
图2 一个路网
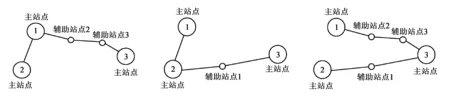
图3 子网集合
1.2 数据处理
为提高数据运算效率,采用分块式处理的方式,主要包括对路网的结构、路网节点属性信息的处理和信息输入接口的设置。对路网的拓扑结构采用序列化的方法存入硬盘中,路网节点属性信息存放在Access数据库中,并通过信息输入接口实现对拓扑结构进行增加、删除、修改、保存。图3为以一个路网(图2)的子网集合,其中路网的主站点代表道路的交叉口,辅助站点是相邻交叉口之间的弯道点。
通过微软基础类库(Microsoft Foundation Classes,MFC)中已有的CTypedPtrArray数组类模板实现路网的存储、动态创建新元素、统计元素个数等功能。同时,通过数组类的封装,把整个网络划分为各个子网的集合,每个子网均是数组类的一个元素,即包含一个节点与其所关联的所有连接信息,这样的改变无疑使网络结构变得更为清晰,而且又充分利用了MFC本身所拥有的标准类。
数组类CTypedPtrArray
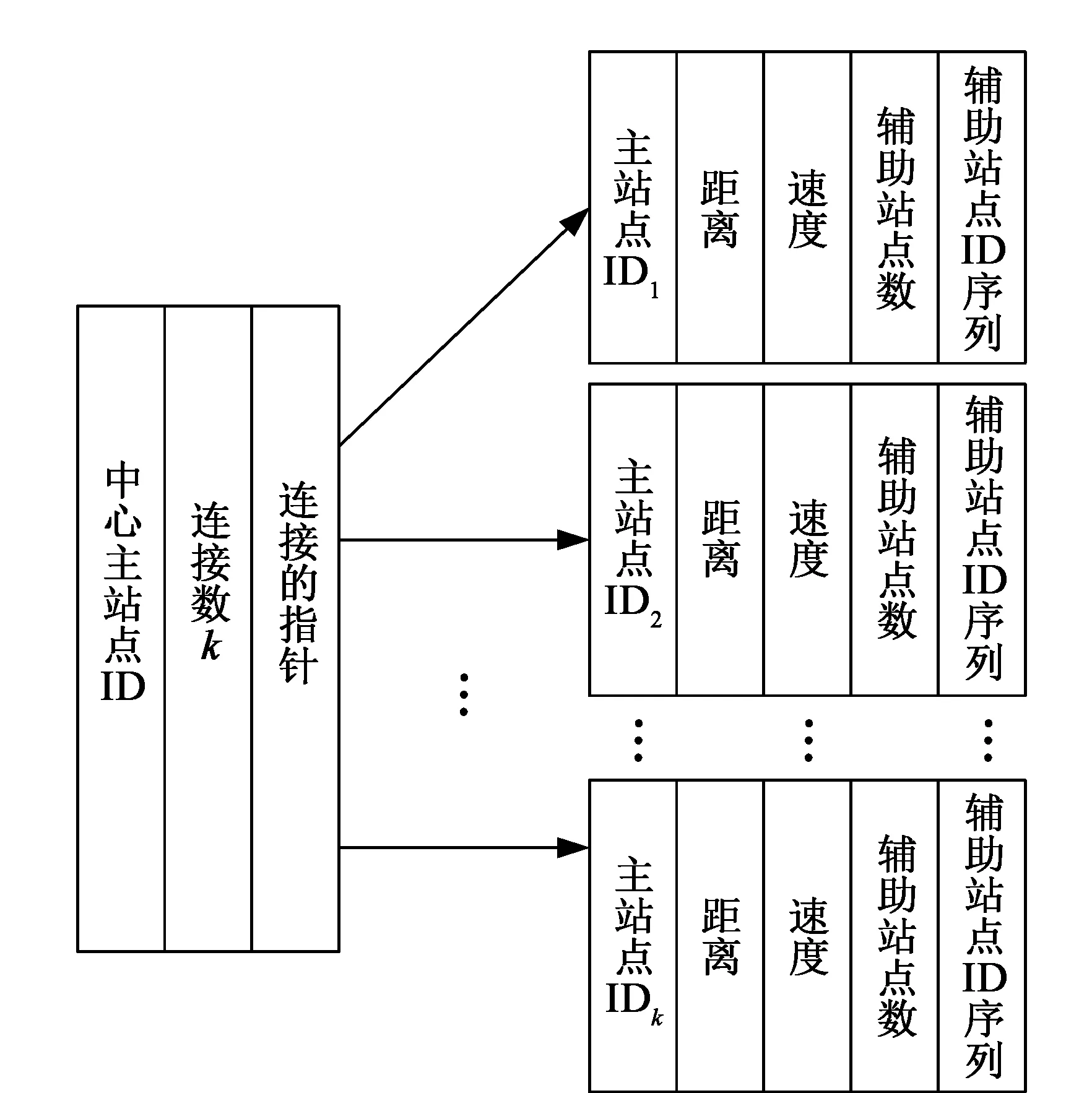
图4 子网的数据存储方式
这里的距离默认的是路程,行驶的速度用于衡量两主站点之间路段的路况拥挤度,根据现实生活中各电子地图的经验,分别以0~10 km/h、10~30 km/h、30 km/h以上代表路况的拥堵、缓慢、畅通。
本系统是选用开放数据库连接(Open Database Connectivity,ODBC)关系型数据库设计的,在系统中设计相关的数据库包含如下3步:
(1)建立应用程序:通过MFC AppWizard建立MFC应用程序。
(2)建立节点属性数据库:Access文件作为系统的节点属性数据库,在文件中建立两张数据表,分别是主站点表、辅助站点表,用于存储主站点及辅助站点的属性信息。主站数据表主要包括节点ID、节点坐标、节点所在街道名称,其中ID为整型,作为主站数据表的唯一标识符。辅助站点表和主站数据表结构一致,这样将提高对数据库的可操作性。
(3)建立ODBC数据源:进入Windows系统中的管理工具选项,在ODBC中添加一个基于“Microsoft Access Driver(*.mdb,*.accdb)”的驱动程序,并在下一步操作中命名数据源名称为“站点信息”,同时把第(2)步中建立的站点信息文件作为对象,通过以上步骤,即可完成对数据库的建立与连接。
2 过必经点的最短路径设计
本文通过Dijkstra算法求解过K个必经点的N条最短路径算法。
2.1 基本原理
对于过K个必经点的N条最短路径算法,必须先求得过第一条K个必经点的最短路径,然后再通过断开第一最短路径所形成的子图集对应的最短路径集合求第二最短路径,如此循环以致求得第N条最短路径。
设G=(V,E)是一个带权有向或无向图,该图是由节点和相连的弧线组成,两个节点之间的不同连接方式组成了两点间所有的路径,每条路径都与其所在的子图相关,子图可以是原图断开某些节点之间的连接或去掉若干个节点以及与这些节点相关的连接组成。在一个子图中求过K个必经点的最短路径,可通过分段求解每一种排列的路径后,去路径最小值来确定最终的最短路径。
对于一个没有孤立节点的子图,每两个节点间存在最短路径。假设图中无孤立节点,那么从起始节点到目的节点之间存在若干条路径。对于每一条路径,该路径有多少段(不同节点之间的连接)就可以通过断开每一段形成多少个子图,这些子图中从起始节点到目的节点的路径集合相并再并上原图中被断开的这条路径所形成的集合,就等于原图中起始节点到目的节点之间的路径集合[3]。根据以上原理可知,只要在子图中,起始节点和目的节点之间存在路径即是存在最短路径。故保持子图所有节点和原图一致,只是断开路径的不同,在原图找到两点之间的最短路径后,断开这条第一最短路径后形成的众子图都分别存在起始节点和目的节点之间的最短路径,倘若两节点之间还存在连接。对于原图来说第二最短路径便是这些形成子图的最短路径中最短的,如果所有子图中都不存在这两点间的路径时,表明只有第一最短路径这一条。
因此,求过K个必经节点的N条最短路径就是对每次找到的过K个必经点最短路径的子图进行再次分割,并且和已有子图存在的过K个必经点的最短路径进行一一比较,找出最短的,这样不断地重复执行,并在执行过程中去除重复的路径,直到路径条数达到满足或者已无路径为止。
2.2 算法步骤
过K个必经点的N条最短路径步骤如下:
(1)求出第1条过K个必经点的最短路径。
(2)创建一个数组类arrWebShortestPaths,对第一条过K个必经点的最短路径进行添加;在该过K个必经点的最短路径对应的子图中(第1条对应的子图为原图),保持所有节点不变,按照该条路径进行分段断开,从而形成若干个对应的子图,计算每个子图对应的过K个必经点的最短路径;创建arrFormSubnetInfo数组类,用于把每个子图对应的最短路径的长度和从原图形成该子图所断开的某两个节点之间路段进行保存。
(3)删除arrFormSubnetInfo此次中形成新子图的母图记录,比较arrFormSubnetInfo每个元素对应最短路径的长度,求最小长度,找出该元素,并从记录中可知其最短路径对应的子图是通过原图断开哪几段路段后形成的。创建一个数组比较类arrWebShortestPaths,用于新找出这条过K个必经点最短路径,和已存储的所有最短路径比较,若存在相同的,则不进行添加,反之,则添加。
(4)判断数组类arrWebShortestPaths中已有的最短路径是否有存在重复路段,把没有重复路段的用整型变量作一标记,返回执行第2步,直到该标记值和所需的最短路径条数N相等或者已无最短路径为止。
3 数值实验
图5为模拟道路情况的数据集,对其进行最短路径求解。
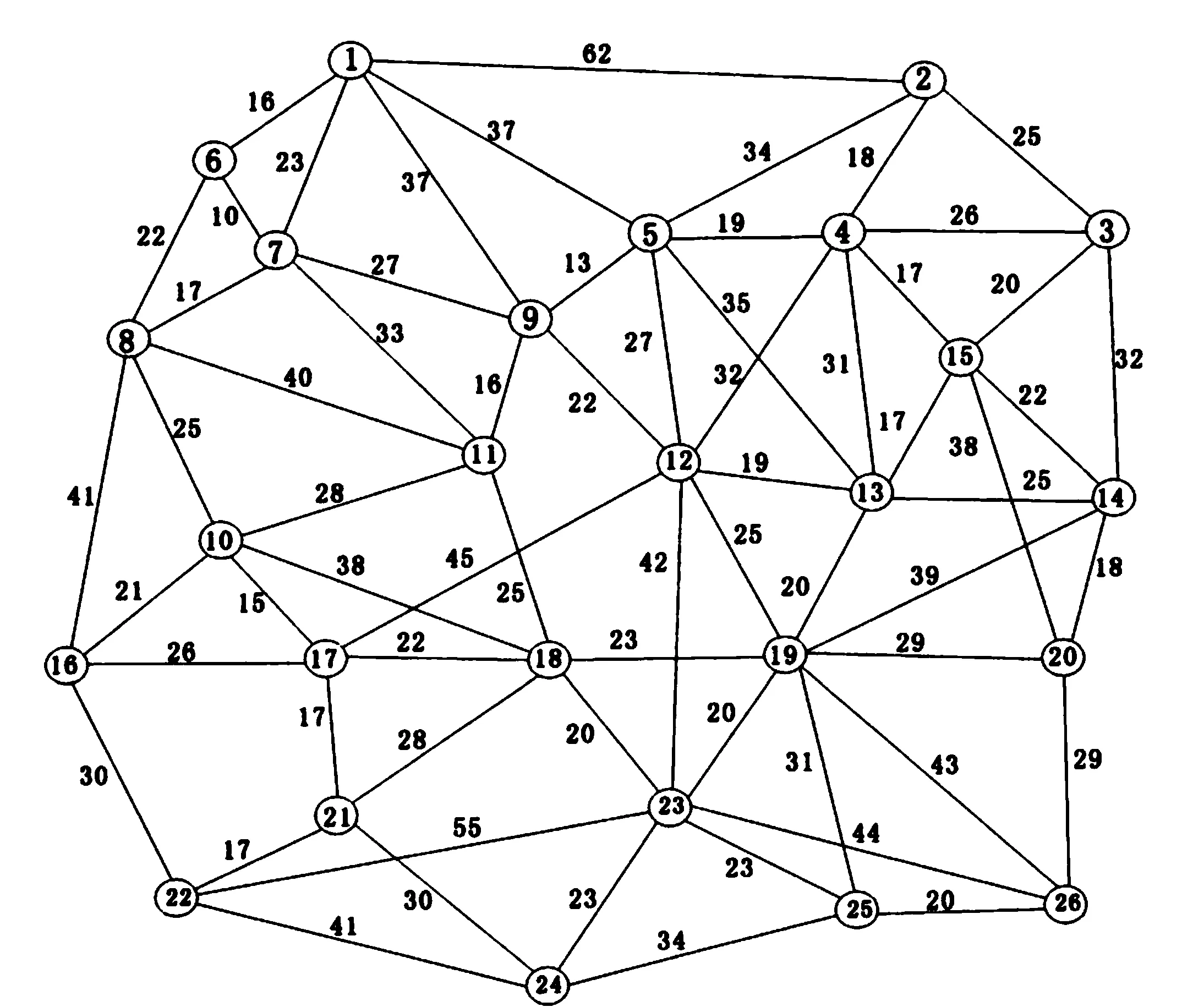
图5 26节点数据集
3.1 无必经点的前N(N=20)条最短路径
以节点2为起点,22为终点的无必经点的前N(N=20)条最短路径,求解结果如表1所示。
从实验结果可以看出,在这20条路径中,结果均不存在重复路径,更不会在同一路径中重复出现同一路段,这表明算法的思想和设计的程序是完全正确的。
3.2 过K个必经点的N条最短路径
以节点2为起点,22为终点,随机选择K(K=1,2,3,4)个必经点的前N(N=1,2,3,4)条最短路径,求解结果如表2所示。
通过表2可以确认,本文算法实现的过K个必经点的前N条最短路径,在K、N分别为不同值时,对应的N条路径均是表1中已得到验证的前20条最短路径中最短的前N条;同时,对比过必经点17和过必经点13、17的第一最短路径可知:如果增加的必经点不是过原必经点路径上的点的话,必然会随着必经点的增加,而使路径总长度变长。由此可见,该算法完全可以保证理论上的过K(K小于5)个必经点的前N(N小于5)条最短路径的实现。
本文使用的过必经点的最短路径算法,实质上是通过反复迭代基本Dijkstra算法改造而来的。因此,在时耗上受基本Dijkstra算法时间复杂度的影响,即受赋权图规模的影响,赋权图的结点越少,边数越少,时间耗费越少,反之,则越多;而且随着路径条数和必经点个数的增加,时耗会成倍地增长。本文采用的算法在包含必经点的情况下几乎可以完全保证理论上的前N条最短路径的精确性,但是,在求解时也会由于起始点、必经点及终止点之间的连接关系不同而产生时耗上的差异。在有必经点的情况下,由于必经点在起始点和终止点的相对位置上的差异,可能会引起算法路径搜索上较大的区别,从而在时耗上也会相差很大,而且这种差别会随着必经点或路径条数的增加而变得更明显。

表1 无必经点的前20条最短路径
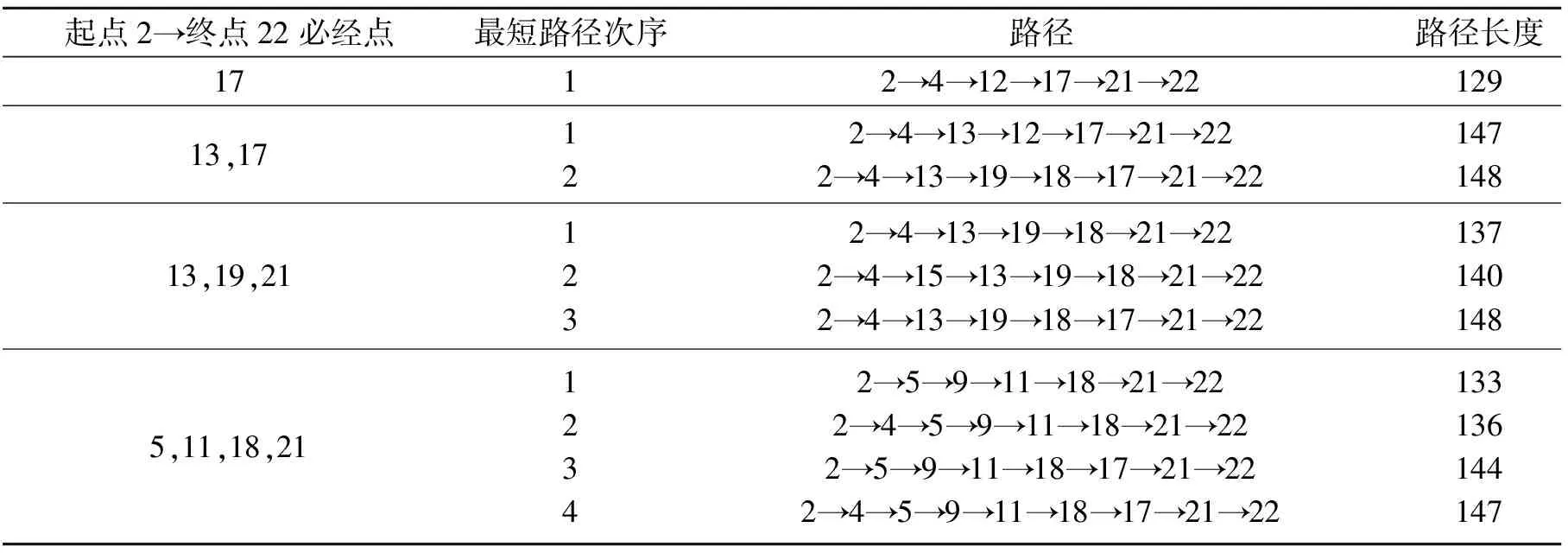
表2 过K个必经点的N条最短路径
4 结论
本文基于Dijkstra算法,设计了过K个必经点的前N条最短路径算法,通过数值实验分析,验证了该条件下理论上过必经点的前N条最短路径的正确性,为过K个必经点的前N条最短路径问题的算法切实可行提供了基础,有效扩充了可行路径的数量,解决了实际中交通诱导系统存在的问题,可以满足用户选择需求。但是智能交通诱导系统是一个非常庞大的系统,本文所涉及到的研究仅是其中的一小部分,建立一个完善的智能交通诱导系统是一个相对复杂的过程,需要投入较多的资源进行开发。在城市交通线路日益增加的今天,智能交通诱导系统的发展拥有非常广阔的前景。
