隧道通风中轴流风机并联运行安全性研究
2020-07-01冯志勇
宋 雕,李 喆,冯志勇,兰 海
(1. 四川川交路桥有限责任公司,四川 广汉 618000;2. 长安大学道路施工技术与装备教育部重点实验室,陕西 西安 710064)
随着我国交通运输业的发展,修建的山区公路中隧道占比越来越大。在隧道沥青路面铺装施工过程中,高温沥青混合料会释放大量的有毒气体,严重影响作业人员的身体健康和施工进度。隧道中若存在一定浓度的瓦斯气体,还会给施工带来安全隐患[1]。在隧道运营过程中,也存在着车辆排放的有害气体,对长时间停留在隧道内人员的身体健康产生威胁[2]。因此,无论在隧道施工还是隧道运营过程中,通风都是关键问题[3]。隧道通风通常采用2台轴流风机并联运行,但由于其叶片自身结构、管网阻力特性的变化等因素,导致其在隧道中工作时可能会出现失速甚至是喘振现象,对风机造成破坏,影响其运行安全[4-6]。
许多学者对轴流风机运行安全性进行了研究。周静等人分析了轴流风机的喘振机理并提出了一些预防措施[7];李春宏通过实际案例分析了轴流风机出现喘振的原因[8];王明奎、李文英对发生失速与喘振的轴流风机进行了数值模拟,并分析了风机内部流场特性[9]。现有资料多是针对单台轴流风机发生失速及喘振的情况进行研究,而关于轴流风机并联运行安全性的研究相对匮乏。2台风机并联时,彼此之间的相互作用会诱导失速及喘振现象出现。为研究风机并联失速及喘振问题,本文通过CFD(计算流体动力学)对轴流风机并联运行进行仿真模拟,以确定设置风机工作参数的合理范围以及风机最佳安装位置,为实际工程提供参考。
1 轴流风机并联工作分析
1.1 轴流风机运行原理
单台轴流风机以一定转速运行时,其风机性能曲线是由无数组流量和对应的压力值组成。风机在性能曲线上哪一点工作,取决于所连接的管路特性,即整个隧道的阻力特性。

图1 轴流风机运行原理图
如图1所示为轴流风机运行原理图,其中P为风机全压,Q为风机流量,ab为风机特性曲线,曲线1、2、3为管网特性曲线,风机特性曲线与管网特性曲线的交点为风机此时的运行工况点。当管网特性改变时,风机的运行工况点也随之改变,达到自动平衡。当增大管网阻力时,风机运行工况点由1移动至2,此时压力增加,流量减小。当减小管网阻力时,风机运行工况点由1移动至3,此时压力减小,流量增加。可以看出,轴流风机运行工况取决于管网特性。
1.2 轴流风机并联运行原理
图2为型号相同、运行转速相同的2台轴流风机并联运行的工作原理图。其中P为风机全压,Q为风机流量,Ⅰ为单台轴流风机工作时的特性曲线,Ⅱ为采用2台风机并联运行时的特性曲线,Ⅲ为管网特性曲线。其性能曲线满足如下条件:在同一压力条件下,并联运行时的流量为单台风机运行时的2倍。可以看出,在同一管网阻力特性下,采用2台风机并联时流量大幅度提高,但总风量小于2台风机风量之和。

图2 轴流风机并联运行原理图
在长大隧道沥青路面铺装过程中,由于隧道横断面积大,通风所需风量大,单台风机风量难以满足需求,此时可增加1台或多台风机并联运行,以提高总风量,满足隧道施工通风需求[10]。
2 轴流风机失速及喘振现象分析
由于轴流风机叶片的特殊结构,导致轴流风机特性曲线具有驼峰,其峰值点B右侧为稳定工作区,峰值点左侧为不稳定工作区[11-12],如图3所示。
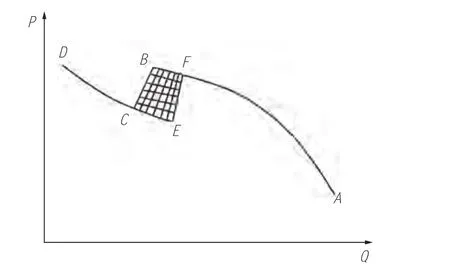
图3 典型轴流风机性能曲线
图3为典型轴流风机性能曲线,其中P为风机全压,Q为风机流量。风机最初运行在AB段的稳定工作区,当系统阻力增加时,风机流量相应减小。若流量减小至低于点B对应流量时,风机叶片气流不稳定,风机进入失速状态。轴流风机在点C回到“半稳定”的第二条特性曲线上,此时流量可以进一步减小,同时阻力又开始增加。若系统阻力降低使风机的工作点从点D移动回到点E,随着进一步降低系统阻力,工作点将会从该点跳回到稳定工作点F。由B、C、E、F组成的区域是风机运行极其不稳定的区域,气体具有不确定的流动性。在不稳定区域内,当轴流风机发生失速时,风机压力突然降低。由于管网系统容量较大,使得管网中压力大于风机出口压力,风机无法向系统排出风量,反而系统中的风量要向风机内部倒流。随后风机自动调节系统又向管网输送气体,管网压力回升。如此不断循环,就会形成喘振[13]。
根据上述分析,风机能否平稳运行取决于管路系统阻力的变化。若风机出口所受的外界压力大于风机输出的出口压力,风机会发生失速现象,并进一步形成喘振[14]。
当2台轴流风机并联运行时,风机内部流场及回流区的变化相较于单台轴流风机运行要复杂得多。尤其当2台风机运行参数不同、输出流量与风压有较大差异时,对并联工况下实际流动情况进行监测十分困难。
3 轴流风机并联运行仿真分析
2台轴流风机并联工作时,对于其中一台风机而言,另一台风机的输出流量与风压相当于是管路系统的一部分,2台风机之间相互影响。为研究风机之间的相互作用对其发生失速及喘振现象的影响,采用FLUENT软件对2台风机并联工况下的系统流场进行仿真分析。
3.1 数值模型
隧道轮廓参数参考米仓山隧道,隧道模型高8.6m,宽15m,长60m。风机尺寸参考SDS-12.5射流风机,风机截面直径1460mm。由于本仿真仅观察风机出口外界压力数值,为简化仿真模型,使用2个圆形截面表示风机,2台风机对称安装在隧道入口截面高5m处,风机相距5.6m,采用三维建模软件Unigraphics NX对隧道及风机以10:1比例建模。将模型导入ANSYS mesh中进行网格划分,如图4所示。

图4 隧道网格划分模型
通过计算流体动力学FLUENT软件采用标准κ-ε双方程模型,并对模型进行求解[15-16]。边界条件设置如下:
(1)隧道壁面设置为墙面wall,参数保持为默认数值。
(2)隧道进口与出口均为速度进口边界,本仿真不考虑隧道内外压差及自然风影响,设置为Velocity-inlet,速度取0m/s。
(3)2台风机截面为压力出口边界,设置为Pressure-outlet,压力数值根据试验条件设定。
3.2 并联风压比
将左侧风机设置为高压风机,出口压力PH依次为0Pa、120Pa、140Pa、160Pa、180Pa、200Pa、240Pa、280Pa、320Pa、360Pa,将右侧风机设置为低压风机,出口压力PL始终为0Pa。对求解结果中右侧风机外界压力监测值P进行记录,记录结果如表1所示。

表1 第1组右侧风机外界压力监测值/Pa
表1中监测值即为右侧风机在左侧风机风压下不发生失速的临界风压值。保持左侧风机压力数值同上,将右侧风机出口压力数值依次设置为相对应的临界风压值,其他参数不做变化,再对求解结果中右侧风机外界压力进行记录,如表2所示。

表2 第2组右侧风机外界压力监测值/Pa
再次进行上述操作,将右侧风机外界压力进行记录,如表3所示。
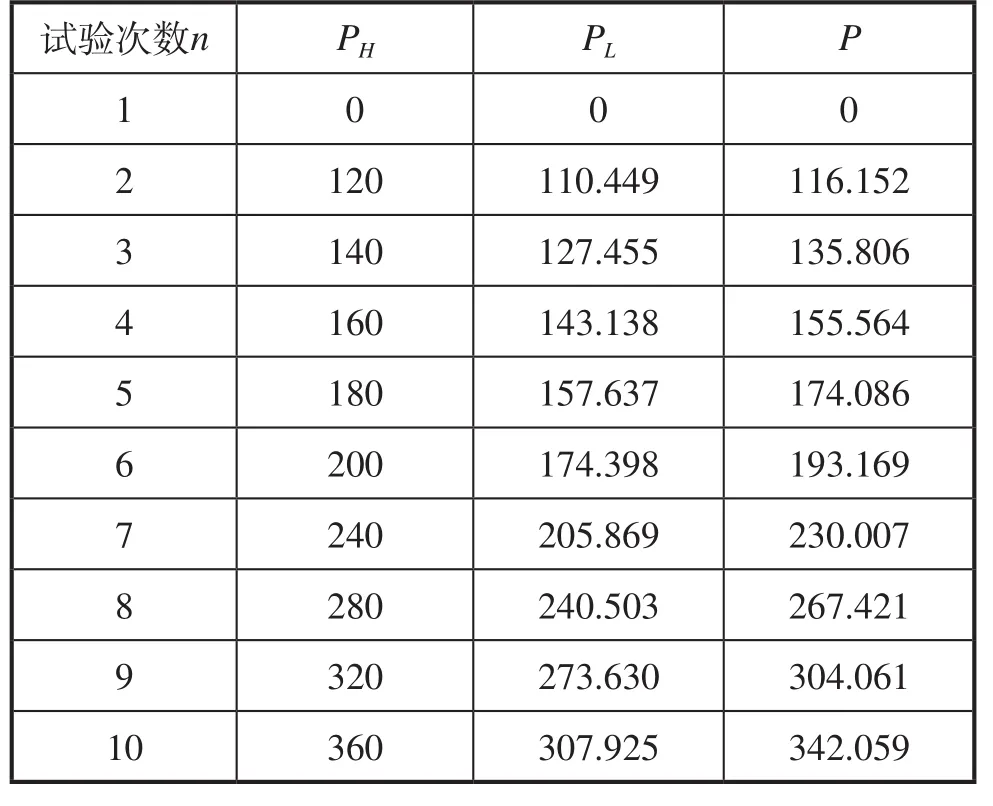
表3 第3组右侧风机外界压力监测值/Pa
根据表1-3中数据可以看出,当低压风机同高压风机并联工作时,低压风机外界压力始终大于低压风机出口压力,因此低压风机一直存在发生失速的可能性。以左侧风机出口压力为横坐标,右侧风机外界压力监测值为纵坐标,将上述3组数据绘制在同一坐标系中,如图5所示。

图5 右侧风机外部压力监测值与左侧风机出口压力关系
从图中可以看出,对于同一隧道的固定位置,一侧风机出口压力与其对另一侧风机外界压力影响呈线性关系。对3组数据进行拟合,拟合结果分别为P=0.605PH,P=0.842PH,P=0.947PH,其中P/PH=0.605为仿真位置风机并联工作发生失速的临界风压比。定义风压比φ为低压风机出口压力PL与高压风机出口压力PH的比值,如式(1)所示。

因此风压比φ取值范围为φ∈[0,1]。当低压风机出口压力PL为0时,风压比φ为0;当低压风机出口压力PL与高压风机出口压力PH相等时,风压比φ为1。
3.3 失速可能性大小评估
以下就不同风压比时风机发生失速可能性大小进行对比分析,采用失速因子δ对失速可能性大小进行评估。失速因子δ表示在某一风压比下,风机外界压力超出风机出口压力的压力值对风机失速情况产生的影响。δ越大表明当前风压比下风机越容易发生失速,反之则表明当前风压比下风机越不易发生失速。其计算方法如式(2)所示。
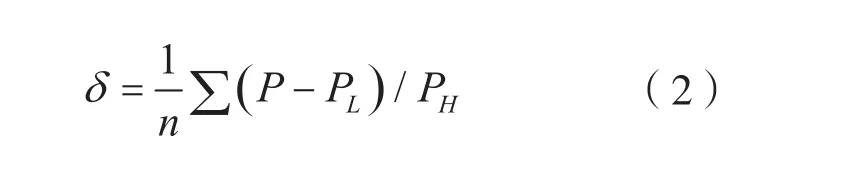
选择不同风压比进行数据记录并计算失速因子,计算结果如表4所示。
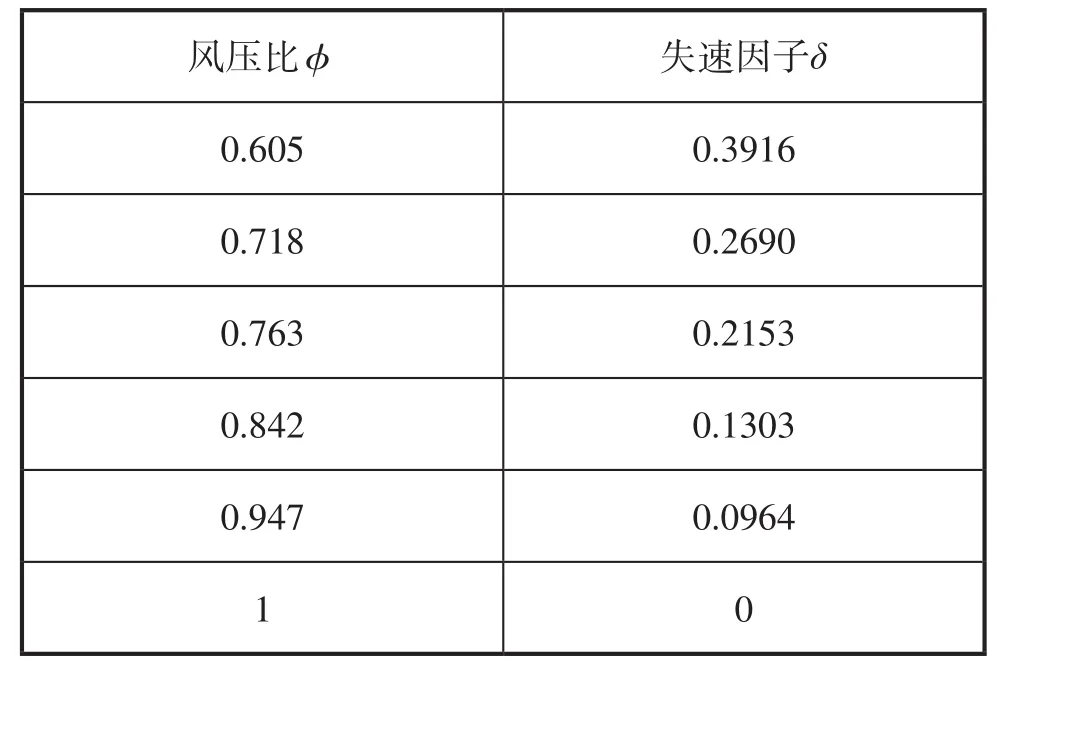
表4 不同风压比下的失速因子
由表4可知,2台风机并联风压比φ越大,即2台风机压差越小,失速因子δ越小,风机越不易发生失速,难以形成喘振现象,风机工作平稳;当风压比φ为1,即2台风机输出压力相同时,失速因子为0,表示从理论上讲,此时风机不会因外界压力而发生失速和喘振现象。因此在实际工程应用中,当2台风机并联工作时,为保证风机能够平稳工作,应将2台风机风压比尽可能设置大一些,最小不低于该位置的临界风压比。
4 并联安装位置对轴流风机喘振影响
隧道内风机并联工作时,彼此之间的相互作用与二者的布置位置具有某种关系,同时风机与隧道作为一个系统而言,隧道内壁对风机出流也会产生一定的影响[17]。为得到2台风机并联的最佳安装位置,以下对2台风机间距以及风机安装高度分别进行仿真分析。
4.1 2台风机间距对临界风压比的影响
将2台风机对称布置在距离隧道路面高4.5m处,将风机间距依次设置为3.0m、4.0m、4.5m、5.0m、5.5m、6.0m、7.0m、9.0m,使用与前述相同的参数设置方式与数据采集位置,将不同风机间距的临界风压比记录在表5中,并根据数据绘制曲线,如图6所示。

表5 不同风机间距下的临界风压比

图6 临界风压比与风机间距关系
由图6可以看出,2台风机临界风压比与风机间距关系曲线有极小值点,存在最佳风机间距。临界风压比在2台风机间距5.0m时达到最低值0.618;当2台风机间距由5.0m逐渐减小时,临界风压比逐渐增大。这是由于2台风机间距越来越小,风机相互间的作用越来越明显,高压风机对低压风机的干涉作用变强,如图7所示。当2台风机间距由5.0m逐渐增大时,临界风压比也增加。这是由于风机间距增加,隧道边缘墙壁对风机出流的影响越发显著,如图8所示。

图7 风机间距3m压力云图

图8 风机间距9m压力云图
4.2 风机安装高度对临界风压比的影响
将2台风机对称布置在隧道中,风机间距为6.0m,安装高度依次设置为3.5m、4.0m、4.5m、5.0m、5.5m,使用相同的参数设置方式与数据采集位置,将不同风机安装高度的临界风压比记录在表6中。
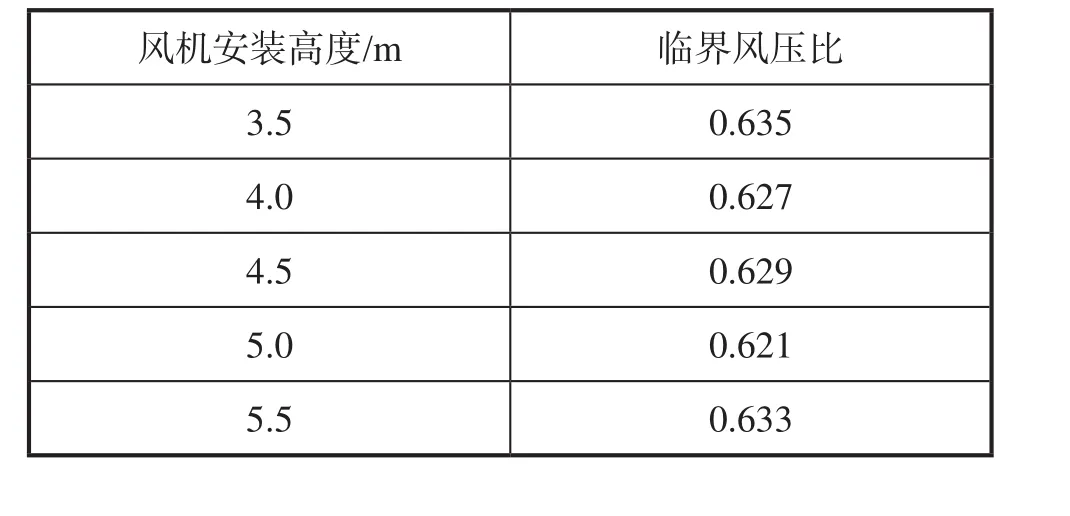
表6 不同安装高度下的临界风压比
由表6可知,当风机安装在5.0m处时,临界风压比达到最低值0.621;当安装高度由5m增加或减小时,临界风压比均呈上升趋势。这是由于过高的高度会使风机与隧道顶部墙体距离减小,过低的安装高度会使风机与隧道路面的距离减小。隧道顶部墙体与隧道路面均会对风机出流的外部流场产生较大影响,从而导致临界风压比上升。
5 结论
在隧道通风过程中,轴流风机并联时流场相对复杂,发生失速甚至喘振现象的可能性较高。本文通过FLUENT对风机并联工作进行仿真分析,得到以下结论:
(1)2台风机并联工作时,对于同一安装位置来说,一侧风机出口压力与其对另一侧风机外界压力的影响呈线性关系。风压比越大,失速因子越小。风机工作发生失速的可能性越小,工作越稳定。当风压比为1,即2台风机风压相同时,风机不会因外界压力而出现失速现象。
(2)2台风机并联工作时,风机安装位置对临界风压比有较大影响,存在最佳安装位置,在该位置上风机临界风压比最小。仿真结果表明,对于本文所述隧道模型而言,2台风机间距5m,且风机安装高度为5m处是最佳安装位置。
