动态电路的戴维南分析法及数值可视化模拟*
2020-07-01付酮程李智
付酮程 李智
(信阳高级中学 河南 信阳 464000)
戴维南(Thevenin)定理表述任何一个线性含源二端网络总可以用一个恒压源Us和一个内阻R0串联来等效代替,替换后电路参数及特性不变,该理论在复杂电路简化中尤其实用[1~3];Simulink工具箱中Simscape在电路可视化和数据挖掘中运用广泛,直观地让学生“看到”动态电路的演变过程,聚焦极值点和暂态瞬间,有助于学生构建物理情境和理论验证.
【例1】如图1所示,定值电阻R1,R2,R3,R4的阻值均为R0,理想电压表读数U,变化量的绝对值ΔU,理想电流表读数I,变化量的绝对值ΔI,在滑动变阻器的滑动端自右向左滑动的过程中,下列判断正确的是( )
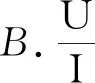
答案:A,B,D.
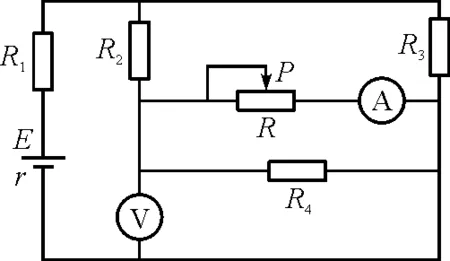
图1 例1电路图
题中选项A,B,C可由闭合电路欧姆定律分析知,I干路↓,U内↓,U外↑,IR3↑,IR2↓,UR2↓,IR4↑,故IR↓,考虑到IR2↓,因此变化幅度|ΔIR4|<|ΔIR|,因此
针对选项D除定性分析外,我们尝试定量计算,计算过程如下.
以滑动变阻器两端为二端(a,b)网络,其余部分等效为电压源,外电路仅为滑动变阻器,如图2所示,由
Ed=UR+Ird
知
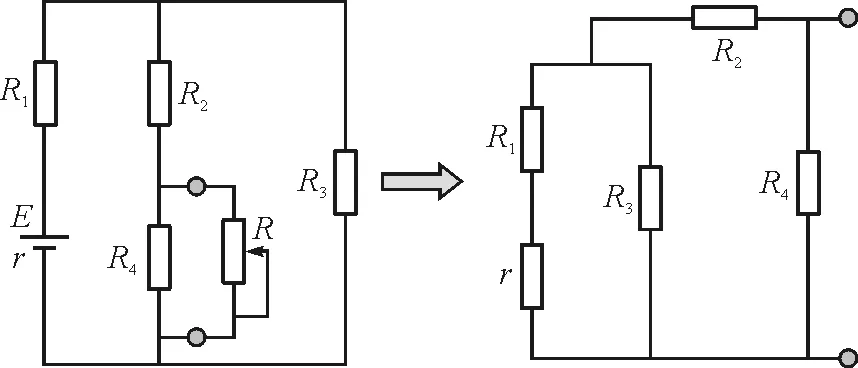
图2 例1电路的戴维南等效电路图
【例2】如图3所示,R0和R2为两个定值电阻,电源的电动势为E,内电阻为r,滑动变阻器最大阻值为R1,且R1>(R0+r).现将滑动变阻器的滑片P由b端向a端滑动,关于理想电流表A1和A2示数变化情况,下列说法正确的是( )
A.A1示数不断减小
B.A1示数先减小后增大
C.A2示数不断增大
D.A2示数先增大后减小
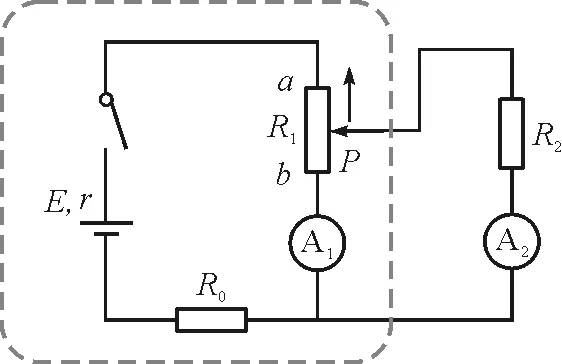
图3 例2电路图
滑动变阻器并联式接法是中学物理常见模型,随着滑片由b到a滑动,回路串并联电阻变化将影响干支路电流,这里我们将通过理论计算得出结果.
(1)戴维南定理计算
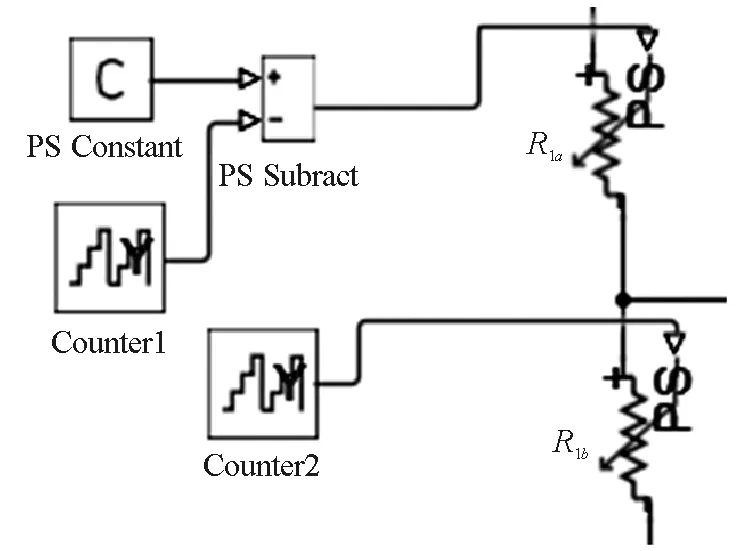
将图中虚线框中部分等效为二端网,采用等效电源(Ed,rd)替代,电路如图4所示,框中部分被M和N两端点左侧电路替代:令滑片P及上方部分电阻为R1a,下方至b端电阻为R1b(R1=R1a+R1b).电路结构为R2与R1b并联后再与(r+R0+R1a)串联,随着滑片向上滑动,R1a减小R1b增大;等效电动势等于原电路M和N端开路时电压
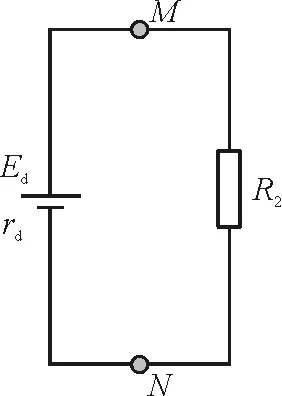
图4 例2电路简化后的等效电路图
等效内阻为左侧网络中电源置零时所对应的无源网络总电阻,即为R1a,r及R0串联后再和R1b并联
rd=R1b∥(R1a+R0+r)=
环路电流即通过R2的I2
当变量R1a减小时电表A2示数持续增加;考虑到原电路中I2R2=I1R1b,所以
由于
取等条件
即
变化中电表A1示数有最小值,示数变化先减后增,故题目答案为选项B,C;电路简化后结构清晰,便于理解且方法通用.
(2)MATLAB仿真模拟
Simulink[4,5]是MATLAB中的一种可视化仿真工具,是基于框图设计环境实现动态系统建模、仿真和分析的一个软件包;在直流动态电路分析时,首先在库(Library)中找到元件,按照电路图将元件连接起来.用传感器测量电流、电压时,需要转换模块(PS-Simulink Converter)将物理模型信号和仿真模型信号对接;此外,模拟系统要连接Solver Configuration模块,注意回路接地.用MATLAB软件对例2进行仿真模拟,程序流程图如图5所示.

图5 例2MATLAB仿真模拟程序设计流程图
元件参数方面,直流电压源(E=10 V,r=2 Ω),电阻R0设为18 Ω,R2设为20 Ω,并联式滑动变阻器R1总电阻50 Ω,两电表为标准物理元件.
程序设计方面,涉及电表变量分别为I1和I2,滑动变阻器R1采用两个可变电阻(Variable Resistor)构成,对应变量R1a和R1b,并由计数器(时间步进为0.1 s)分别控制两变量等幅(±1 Ω)增减,其中计数器1数值和定值50做差实现R1a变量减小,计数器2赋值实现R1b增加;滑片从b到a对应完整变化周期为5 s,R1b|t=10t(0 两电表输出端连接双端示波器,结果由波形面板(Dashboard)展示出来;仿真结果如图7所示. 图6 滑动变阻器在Simulink中的实验方法 图7 MATLAB模拟结果 从图中可以看出电表A1信号流的数值先减后增,电表A2信号流持续增加(非线性).将参数代入理论结果计算得:当 此时,I1有最小值76.19 mA.对比示波器面板如图8所示,可以看到当时间t=3.5 s时,即R1b为35 Ω时最小电流为0.076 2 A,模拟结果和理论一致. 图8 模拟结果中的数值对比 运用戴维南定理简化分析动态电路,能够快速获得解析解,电路结构简单明了.新课程教学实践中牵引学生借由理论分析到数值模拟,能很好地帮助学生构建可视化的“物理情景”[8],让繁复多变的电路参数和临界结点在学生脑中活络起来,深化对问题的洞察能力.