基于STARMA模型的感病松林内松墨天牛成虫发生量预测
2020-07-01周书永丁昌地陈绘画
周书永,丁昌地,陈绘画
(1.浙江省临海市森林病虫防治检疫站,浙江 临海 317000;2.浙江省临海市桃渚镇农业综合服务中心,浙江 临海 317000;3.浙江省仙居县林业局,浙江 仙居 317300)
1 引言
松墨天牛(MonochamusalternatusHope)成虫取食马尾松(Pinusmasoniana)、黑松(P.thunbergii)等树种1~2年生的嫩枝作为补充营养,导致寄主树势衰弱进而引发松墨天牛成虫聚集产卵、过多的松墨天牛幼虫钻蛀导致松树寄主死亡[1],松墨天牛还是我国松材线虫病Bursaphelenchusxylophilus(Steiner&Buhere,1934)Nickle的主要传播媒介。松墨天牛一生的大部分时间都生活于寄主体内,只在成虫时期离开寄主,啃食寄主嫩枝用以补充营养。松墨天牛成虫的林间数量动态变化多有研究[2~5],陈顺立等还用神经网络方法预测松墨天牛的发生量[6],但有关感病马尾松林中松墨天牛成虫的发生量尚未见报道。
时空序列是指在空间上有相关关系的多个时间序列的集合。时空序列建模则是指寻找一种分析时空序列数据的方法,对未观测时空位置的属性进行预测。实现时空序列模型的方法有时空动力学方法、时空相关统计学方法、时空地统计学方法等[7],时空自相关移动平均模型(Spatial Temporal Auto Regressive and Moving Average.STARMA)于20世纪80年代提出,它假设变量是当前位置以及其空间邻接位置过去几个时期观测值与随机误差项的线性组合,根据历史的观测数据建立时空相关-自相关函数得到时空相关性模型[8,9],STARMA模型已在交通、环境、经济等领域都有成功的应用[10,11]。本文基于3个感病松林试验点内松墨天牛成虫的连续时序监测数据开展松墨天牛成虫发生量的预测研究,根据松墨天牛成虫诱捕数量的时间自相关性、空间相关性以及时间空间的互相关性,建立松墨天牛发生量的时空自相关移动平均模型,对松墨天牛发生量进行预测。
2 材料与方法
2.1 试验点概况
临海市位于浙江省东南部,地处28°40′37″~29°04′15″N、120°49′41″~121°42′25″E,东西长为85 km,南北宽为44 km,全市总面积2208.5 km2,其中松林面积为5.9×104hm2,以马尾松纯林为主,3个试验点的概况及悬挂的诱捕器数量详见表1。

表1 3个试验点的概况及悬挂的诱捕器数量
2.2 试验材料及松墨天牛成虫林间动态观测
松树蛀干类害虫引诱剂(规格:300 mL/瓶)由浙江省林业有害生物防治检疫局和中国林业科学研究院亚热带林业研究所研制、宁波中化化学品有限公司生产(2010年后由浙江黄岩鼎正化工有限公司生产),以及与松墨天牛引诱剂配套的小型折叠式诱捕器(2007~2011年4~9月份使用)。松墨天牛性引诱剂F1由浙江农林大学生物农药高效制备国家地方联合工程实验室研制,以及杭州科森农化有限公司与浙江农林大学生物农药高效制备国家地方联合工程实验室研制BF-1型诱捕器(2012~2015年4~9月份使用)。2007~2015年4~9月份,在临海市江南街道、沿江镇及大田街道的马尾松人工林和天然林内,将诱捕器架设在距地面1.5 m、两株相近的马尾松树间铁丝上。诱捕器的间距为80~130 m,单只离林缘40~70 m,3个试验点各架设20只诱捕器。在引诱剂瓶口的包装材料(直径3 cm)上打0.5 cm直径小洞3个。每隔3~4周更换1次引诱剂,收虫的间隔时间为2~7 d,以月为单位进行统计。由于4月的诱捕量太少,故将4月的诱捕量合并到5月。
2.3 STARMA模型
STARMA模型为自回归移动平均(Autoregressive Moving Average,ARMA)模型在空间的扩展,该模型在考虑某观测值所在位置时间序列的同时,也考虑其空间相邻位置的时间序列,从而提高时空序列预测的准确度。
2.3.1 STARMA模型的描述

STARMA模型是针对同一个变量的空间相关性与时间相关性建立的,Zα(t)是由空间点的过去时刻值和过去随机误差值,再加上其空间邻近点的过去时刻值和过去随机误差值影响,空间位置的相关性以空间权值矩阵的形式表示。STARMA模型为:
(1)
式(1)中:p为时间自回归阶数;q为时间移动平均阶数;λk为第k个自回归项空间阶数;mk为第k个移动平均项空间阶数;φkl为需要估计的时间滞后k、空间滞后的自回归系数;θkl为需要估计的时间滞后k、空间滞后的移动平均系数;Wl为l阶空间邻接的N×N权重矩阵,εα(t)是随机变量。
2.3.2 STARMA模型的建立
STARMA模型的建模过程包括数据预处理、模型辨识、参数估计、模型诊断以及预测分析等5步。通过数据预处理,将非平稳时空序列转换为平稳时空序列;模型辨识则是初步确认候选模型;参数估计为求解候选模型的参数;模型诊断则是根据相关指标判断是否接受所建立的模型;模型预测是将建立的模型进行预测并分析模型的预测性能。
设N是二维空间的监测点数,T是观测时间的最大值,则经T次观测,共有总数为NT的观测值,全部观测值的平均值为[12]:
mz=∑∑∑Zαt/NT
(2)
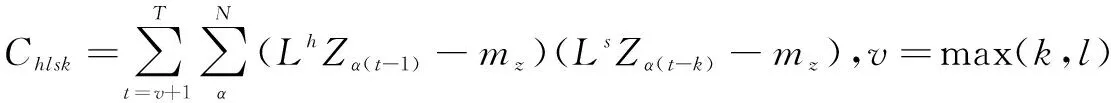
空间权重矩阵是二维空间位置上变量值受其空间邻近位置变量值影响的定量化测度。若研究空间有n个面积单元,其中任何两个面积单元间都存在一个空间关系,则有n×n对关系,因而可以用n×n的矩阵存储这n个面积单元间的空间关系。空间权重矩阵W的具体形式为:
(3)
空间权重矩阵的建立方法有边界法[13,14]、拓扑图法[9]等,用边界法建立的权重矩阵元素为:
(4)
(5)
二维空间某单元的变量值受其邻近空间位置变量值的影响度称空间延迟算子,用L表示,则空间延迟算子L与空间权重矩阵W的关系为:
L0zα=INzα,L1zα=W1zβ,…,Lhzα=Whzβ
(6)
式(6)中:I为单位矩阵,h为矩阵阶数。
3 结果与分析
3.1 数据预处理
将3个感病松林试验点内2007~2013年每年5~9月的松墨天牛成虫连续诱捕数据按下式进行数据预处理,去掉原始观测数据中的线性趋势和周期性趋势:
Zα(t)=Yα(t)+Tα(t)+Cα(t)
(7)
式(7)中:Yα(t)为二阶平稳随机函数,Tα(t)为线性趋势,Cα(t)为周期性趋势。线性趋势和周期性趋势的去除方法详见文献[15,16]。
3.2 STARMA模型的辨识及参数估计
在建立STARMA模型时,通常根据时空自相关和偏相关函数来确定模型的阶数,3个试验点观测值预处理后的时空自相关和偏相关函数见表2、3。
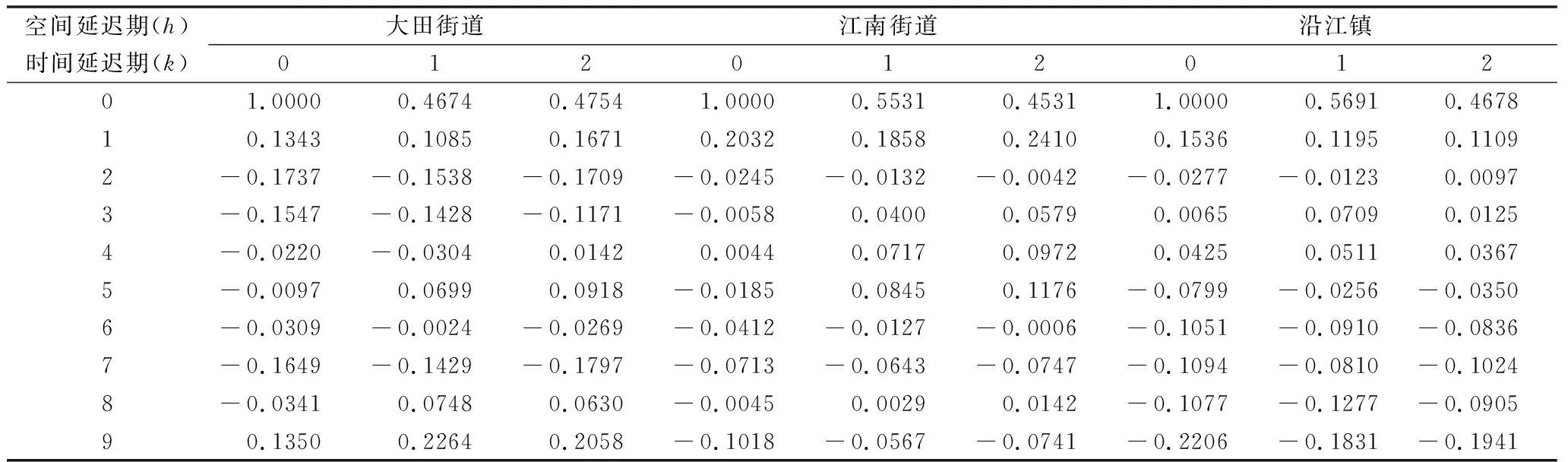
表2 3个试验点的时空自相关函数

表3 3个试验点的时空偏自相关函数
从表2、表3可以看出,无论是时空自相关函数还是时空偏自相关函数,江南街道和沿江镇在时间上都延迟1期后呈截尾趋势,大田街道则在时间上都延迟3期后呈截尾趋势。根据引诱剂诱杀松墨天牛的实际,结合文献13的研究,空间权值矩阵的阶取2。因此可以判断江南街道和沿江镇的数据均为一个1期时间延迟和2阶空间延迟的自相关过程,大田街道则是一个3期时间延迟和2阶空间延迟的自相关过程。对数据预处理后的3个试验点内2007~2013年每年5~9月的松墨天牛成虫连续诱捕数据按式(1)进行最小二乘估计,得到大田街道的方程表达式为:
z(t)=0.2120+0.0847z(t-1)-0.1185z(t-2)-0.0727z(t-3)+0.0428W1·z(t-1)-0.0784W1·z(t-2)-0.0576W1·z(t-3)+0.2339W2·z(t-1)-0.1456W2·z(t-2)+0.0842W2·z(t-3)
(8)
江南街道的表达式为:
z(t)=-0.0985+0.1184z(t-1)-0.0063W1·z(t-1)+0.2641W2·z(t-1)
(9)
沿江镇的表达式为:
z(t)=-0.2221+0.1155z(t-1)+0.0325W1·z(t-1)+0.0407W2·z(t-1)
(10)
3.3 STARMA模型的检验
对模型(8)~(10)的参数进行显著性检验,删除模型中参数检验不显著的自变量,再次进行最小二乘估计和模型参数显著性检验,得到所有自变量都显著的模型为[17]:
大田街道:
z(t)=0.2202-0.0676z(t-1)-0.1274z(t-2)+0.0910z(t-3)-0.1798W2·z(t-2)+0.2445W2·z(t-3)
(11)
江南街道:
z(t)=-0.0985+0.1169z(t-1)+0.2609W2·z(t-1)
(12)
沿江镇:
z(t)=-0.2201+0.1462z(t-1)
(13)
对模型(11)~(13)进行F检验,检验结果为:大田街道,F=14.5927>F0.01(5,500)=3.05;江南街道,F=25.1445>F0.01(2,500)=4.65;沿江镇,F=16.4453>F0.01(1,500)=6.69,说明所设的模型(11)~(13)正确。模型(11)~(13)的残差时空自相关函数和时空偏自相关函数计算结果列于表4、表5。
从表4、表5看出,模型(11)~(13)的残差时空自相关函数值和时空偏自相关函数值都较小,在时间上或空间上都不存在显著的自相关,说明所选择的模型较好地表示了时空数据序列,因而所确定的模型和估计的参数可以预测各试验点内松墨天牛的诱集数量。
3.4 STARMA模型预测结果的检验
设所建模型某月松墨天牛诱捕量的预报值为X1j,实际诱捕量为X2j,则:
Dj=X1j-X2j,j=1,2,…,n
(14)

(15)
服从自由度为n-1的大分布,其中
因此,在显著性水平为α时,可通过比较|t|与tn-1(α/2),来检验假设H0:δ=0和H1:δ≠0。即若|t|
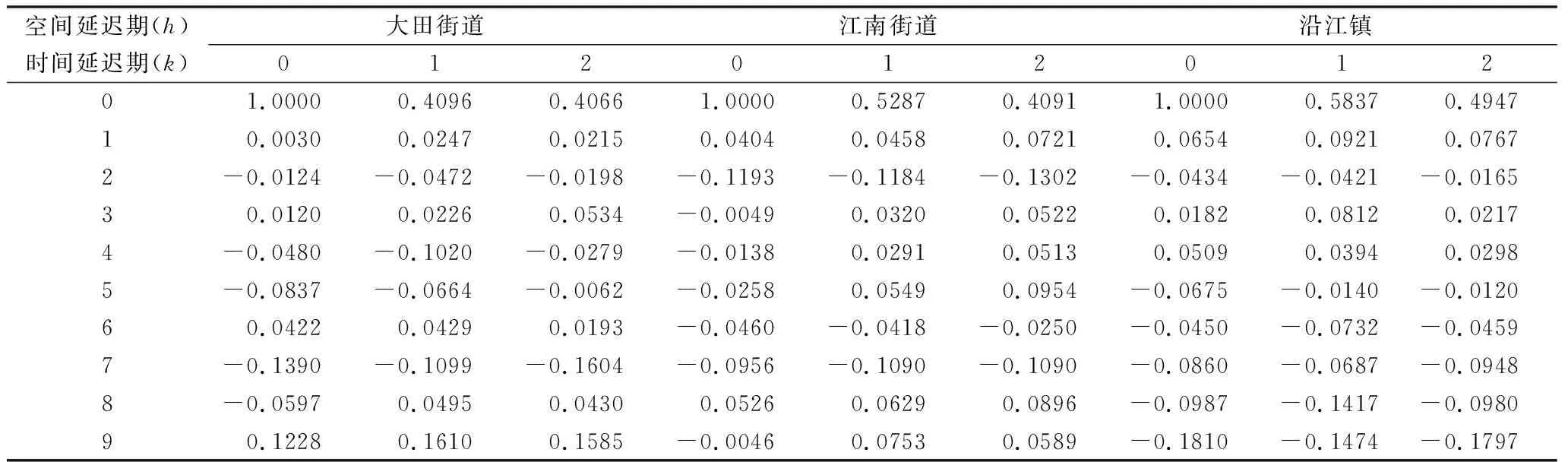
表4 3个试验点残差的时空自相关函数
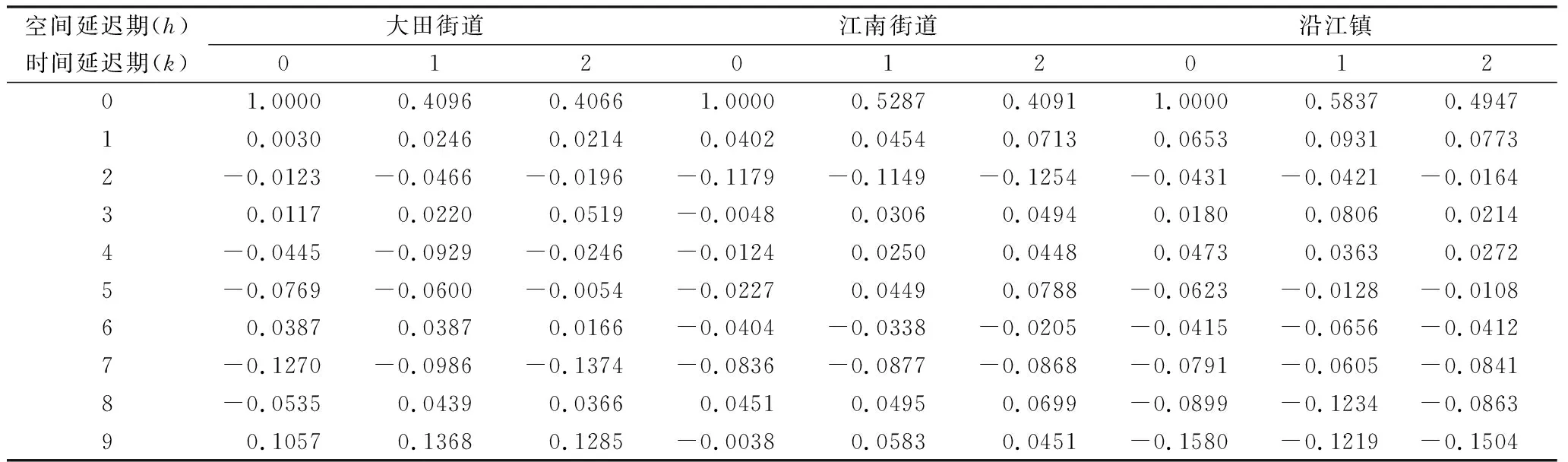
表5 3个试验点残差的时空偏自相关函数
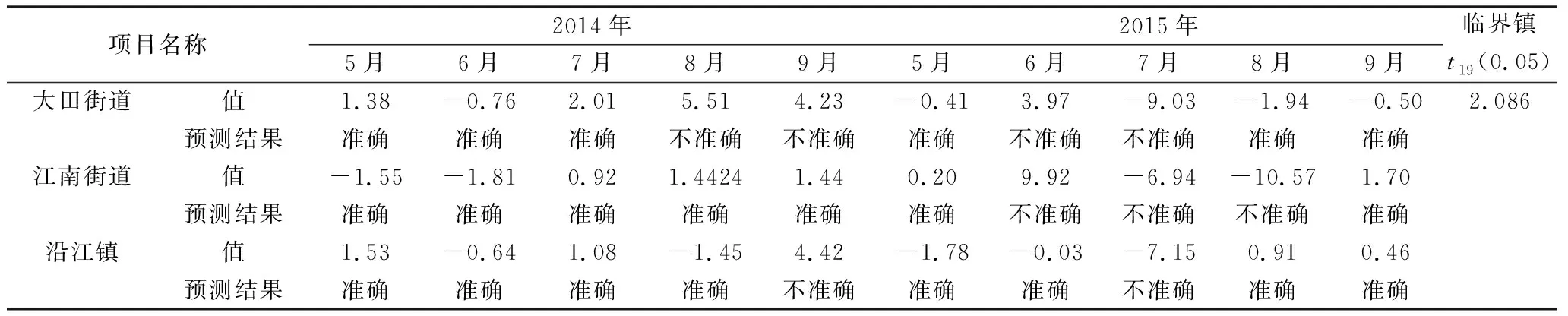
表6 3个试验点未参与建模的2014~2015年每年5~9月松墨天牛成虫的预测结果
从表6可以看出,所建立的模型预测3个试验点未参与建模的2014~2015年每年5~9月的松墨天牛成虫,大田街道预测准确的6次、不准确的4次,预测成功率为60%;江南街道预测准确的7次、不准确的3次,预测成功率为70%;沿江镇预测准确的8次、不准确的2次,预测成功率为80%,平均预测成功率为70%。
4 小结与讨论
本文在考虑感病马尾松林内各松墨天牛诱捕点自身过去与现在、未来的时间关系的同时,还考虑周围相邻诱捕点的过去与该诱捕点未来诱捕量变化的空间关系,从整个感病松林出发,综合评价网络时空拓扑关系,将 STARMA 方法应用到松墨天牛诱捕数量的预测领域中,并借助浙江省临海市2007~2015年3个感病松林试验点来验证方法的可行性,预测3个试验点未参与建模的2014~2015年每年5~9月的松墨天牛成虫诱集数量,平均预测成功率为70%。较高的预测成功率表明了此方法用于松墨天牛诱捕数量预测的可靠性,为松墨天牛的可持续控制提供科学的依据。
STARMA方法可以较好地将时间和空间属性融入到模型中,对网络条件下松墨天牛诱捕数量预测的适应性较强,借助于STARMA 方法进行预测,其平均预测效果较好,但是STARMA 方法还有待改进,如在确定空间权重矩阵过程中,只考虑了诱捕点间的相邻与否,没有考虑相邻诱捕点间距离的远近。在今后的研究中,可以在模型中加入空间距离对诱捕效果的影响,保证模型参数尽可能地反映实际情况,提高模型预测的成功率。
