数学分析中定积分的求解方法

罗睿 贵州民族大学

几何定义：可以理解为在Oxy坐标平面上，由曲线y=f(x)与直线x=a,x=b以及x轴围成的曲边梯形的面积值（一种确定的实数值）。

一、提出背景

在生活中，很多与我们日常生活息息相关的问题需要用数学来解决，以面积为例，比如买房子时需要计算面积，而面积怎么计算就是数学的知识。而通常，能够通过具体的公式来计算的都是规则的平面或立体图形，而那些不规则的图形面积又怎么计算呢？基于此，为了解决就提出了定积分的概念。简单来说，就是利用极限的思想，将曲边梯形分解成若干小矩形，那么曲边梯形的面积就近似等于这些小矩形面积之和，分割越精细，近似程度越高。故为了得到更加精确的接近曲边梯形面积的近似值，必须用到极限这个工具，即小矩形的个数n要趋于无穷。

二、定积分的定义及线性性质

设f(x)是定义在[a,b]上的函数，在(a,b)中任意插入若干分点（这里插入n-1个），a=x0＜x1＜…＜x(n-1)＜xn=b来划分[a,b],在每一个部分区间[x(i-1),xi]中任取一点ξi，作和式，其中，Δxi=xi-x(i-1)，设λ为Δxi(i=1,2......n)中的最大数，即λ=max{Δxi}，(i=1,2......n)，当λ→0时，如果和式σ的极限存在，即，且此极限不依赖于ξi的选择，也不依赖于对[a,b]的分法，就称此极限值为f(x)在[a,b]上的定积分，

三、定积分的求解方法

（一）凑微分法

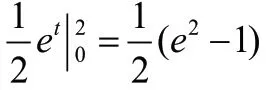
这种换元法就称为凑微分法。

（二）换元积分法

换元公式：f(x)是[a,b]上的连续函数，作代换x=φ(t),其中φ(t)在闭区间[α,β]上有连续导数φ,(t)，当α≤t≤β时，a≤φ(t)≤b，换元积分通常分为代数换元与三角换元。对于换元积分，其实和凑微分的基本思想是一致的。

换元积分的思想就是通过一些简单的代换来计算一些复杂的积分，通常大部分的积分是不能直接计算的，都需要通过一些特殊的技巧来求，有些甚至不止作一次代换。

（三）分部积分法

不定积分中，对于可微函数u(x)和v(x)，有（u v）,=u,v+u v,，则有u v,=（uv）,-u,v，两端作不定积分的运算，得，即，我们就把（1）式称为分部积分公式。而对于定积分来说，如果u,(x) ,v,(x)在[a,b]上连续，则。这就是定积分的分部积分公式。

定积分的应用不仅仅是求解题目，更得和现实生活联系起来，当然，前提是求解出结果。对于任意给定的定积分，求解思路万变不离其宗，注意观察选取合适的方法求解，因为很多的求解方法并不唯一[3]。

四、结语

本文主要通过凑微分法、换元积分法、分部积分公式及其他例子介绍如何求解定积分。定积分是积分的一种，是函数f(x)在区间[a,b]上积分和的极限。一个函数，可以存在不定积分，而不存在定积分；也可以存在定积分，而不存在不定积分。一个连续函数，一定存在定积分和不定积分；若只有有限个间断点，则定积分存在；若有跳跃间断点，则原函数一定不存在，即不定积分一定不存在。