定理教学要唱好“五步曲”

王发成 张硕 张强

关键词：高中数学;优课展评;思维教育

中图分类号：G633.6    文献标识码：B    文章编号：1009-010X（2020）14-0054-03

2019年12月，由北京、天津和河北省数学会联合举办、石家庄市第一中学承办的“京津冀”高中数学高级教师优质课展评与观摩活动，异彩纷呈，深受专家评审组好评。下面，笔者汇总专家组意见和建议，结合具体课例做简单点评，以期抛砖引玉，供同行们参考。

一、现场展示课的主要亮点

本次活动的展示课共涉及到两个课题，分别是人教A版必修5中“1.1.1正弦定理”和“1.1.2余弦定理”。每个课题均安排有14位高级教师，分别借用石家庄市第一中学同层次不同班级的学生现场做课。从整体上看，笔者认为有以下几个亮点：

1.从教学过程看，基本采用“问题驱动”方式开展教学。课堂中，多位老师以定理的“发现→证明→应用”为主线，从发展思维的角度，设计成逐层递进的“阶梯式”问题，将知识点镶嵌于“探究”中，沿着学生的认知轨道展开教学。

2.从教学方法看，基本采用“自主、合作、探究”方式。课堂中，能够基于“生本教育”理念，贯彻“先学后教”、“以学定教”、“因学评教”等原则，实施课前自主学习、课上合作学习、课后智慧学习，讨论交流已经成为教学常态。

3.从教学思路看，层次分明、循序渐进、环环相扣。在定理推导与证明过程中，能够注重基本数学思想、方法的渗透与运用，如特殊化、一般化、类比、数形结合等，思维发展脉络清晰。这使得整节课的架构更加枝繁叶茂，丰满有力。

4.从信息化视角看，注重信息技术与数学课程的深度融合。这是“互联网+”视角下，教师素养的良好体现，符合智能化时代对教师的要求，有利于提高教學的实效性。

二、值得注意并深入研讨的问题

正弦定理隶属命题教学范畴。教学过程中，首先是将命题还原为一个具体问题，然后以这个具体问题为逻辑起点，沿着“导入、证明、解释、整合、应用”的基本套路组织展开学习活动，其本质是“弱化抽象关系”。重点评析两个环节：

（一）导入环节——关注学生的认知基础和思维起点

奥苏贝尔说过：“教育学的一切原理可以归结为一句话，即我们要弄清学生已经知道了什么，并把它作为教学的起点。”例如，关于正弦定理，教师首先要清楚“学生的认知基础是什么？”

基础一：初中解直角三角形和证明三角形全等的相关知识。

基础二：平面向量的运算。从新教材的逻辑体系上看，更加凸显向量在教材中的主体地位，突出向量的工具性及其应用的系统性。事实上，运用向量运算推到正余弦定理，是向量知识应用的典型范例。向量法的关键是从三角形这个“闭环回路”中，联想到式子：。若“移项平方”，可推出余弦定理;若引入一个与某边垂直的单位向量，求数量积，就推出了正弦定理。这个式子学生容易想到，也是正余弦定理向量证明的共同切入点，也能体现出思维方法的一致性。

正弦定理是单元起始课，要用好“章头图”，建议用简短的引言让学生明白学习本章知识的目的和意义。同时，为学生构建起一个较为完整的知识愿景，既见树木又见森林。

例如，在初中阶段，学生对直角三角形进行了定量研究，如勾股定理、锐角三角函数等。关于一般三角形，只是对内角和、面积等少量知识进行了定量分析，更多的是定性研究边角关系，得到了SSS、SAS、ASA、AAS等判定三角形全等的方法，让学生明白了一个基本事实：即“给定三角形的三个角、三条边中的某些元素，这个三角形就是唯一确定的。”

到高中阶段，学生要对一般三角形进行定量分析，也就是解三角形。对应着三角形全等判定，就出现了需要定量研究的4个基本问题：

（1）已知两边和其中一边的对角，解三角形;

（2）已知两角和其中一角的对边，解三角形;

（3）已知两边及其夹角，解三角形;

（4）已知三边，解三角形。

“导入”是首要环节，关系到能否用最短时间激发出学生的求知欲，使学生尽快进入深度思维。有教师提出“科学家如何测量地月距离？日地距离？”并播放视频，展示“金星凌日”现象，介绍我国的“天琴计划”。这种视频导入法具有较强的视觉冲击力，且内容丰富，学生不仅知道“定理的学习是有用的”，而且能从中得到快乐体验，记忆深刻且全面。但时间不宜过长，注意前后呼应。教材上采用“命题发现”式，遵循由特殊到一般、由简入繁的认知规律。

首先，是在学生熟悉的直角三角形中，利用锐角三角函数，得出边角之间的正弦关系，即数学表达式。但对于偏离“预设”程序的其它“发现”，如学生得出边角间的余弦关系，即：cosA=，cosB=，从而，不要直接舍弃。建议用简短的语句智慧处理，如“这里虽得到了一个类似正弦定理的数学表达式，但它不具备正弦定理那种完美的结构特征，也不能推广到一般三角形中去应用，故而没有研究价值。”目的是保护学生的探究意识，让课堂焕发出“动态的活力”，但注意这个过程不要复杂化。

其次，是将上面的式子推广到任意三角形中，验证是否仍然成立。但是，在所有三角形验证是不可能的，这就引出“分类验证”。这里，需要停顿一下，留点时间让学生去初步感知定理完美的结构特征，初步感受其中所蕴含的对称美、和谐美。随着教学展开，要不断地解释、剖析和强化定理的本质属性。例如，有的教师让学生动手画出三角形，实际测量它的三边和三角，通过计算进行实验验证;也有教师用几何画板验证，直观感知，完善猜想。

（二）证明环节——正视学生的能力基础和思维方式

定理教学的核心是发展思维，关键环节是“推导与证明”。一般地，要注意三个问题：一是理清证明思路，认真剖析切入点和主线，归纳步骤;二是揭示其中蕴含的数学思想方法，指导学生亲历证明过程，积累活动经验，这比掌握一个结论更为重要;三是对某些重要定理或公式，宜从多个视角，采用多种方法推理或证明。教学主线要清楚，环节要做到清晰而自然，要将数学知识的学术形态转化为学生学习形态。无论是呈现定理背景，还是解释数学表达式、剖析定理本质，都要做出学生更易接受与理解的活动设计。

例如，关于正弦定理，学生一般会有四种较为典型的思路：

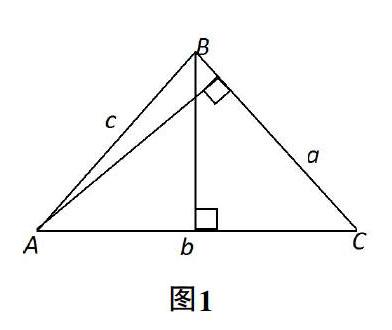
1.几何法：如图1，在一般三角形（分锐角或钝角三角形两种类型）中，验证正弦定理的关键是添加辅助线——作三角形的高，拆分为两个等高的直角三角形，体现的是划归思想。但是，在展示学生思维品质的现状时，我们有的教师驻足时间不够。例如，“为什么要做高？你是如何想到的？”“你是如何想到的证明思路？”等等，这是提升元认知能力的问句，是在挖掘学生思维结果的潜在价值，这里会生成出新的教学资源，应该成为定理教学重点关注的地方，教师要给学生提供足够多的思考时间和足够大的思维空间。

2.借助三角形面积公式证得结论：

2S△ABC=bcsinA=casinB=absinC;

3.如图2，通过做三角形的外接圆，将任意三角形问题转化为直角三角形问题：

a=2RsinA，b=2RsinB，c=2RsinC;

4.向量法：如图3，用向量法证明的关键是作单位向量与向量垂直，再利用数量积运算：即可.

分析：定理教学重点是推理与证明的思维过程。几何法是以逻辑推理为工具进行演绎证明，而向量法是利用向量运算解决问题，两种方法实质上是对立统一的，不可偏倚。让学生从不同的数学角度看问题，经历多种方法的推导过程，有利于学生掌握不同属性的知识体系和不同的工具，有利于学生从不同角度锤炼思维品质和能力。另外，表征出角的正弦后，教师怎样对学生的思维过程进行监控？如何才能得到简洁而自然的证法？怎样对不同证明方法进行筛选和优化？教师要指导学生学会推广与引申、比较与鉴别，并自动将新学定理“同化”或“顺应”到自己的知识体系中来。

总之，定理教学既要关注教学环节的衔接、例题的配备、教学任务能否顺利完成这些基本环节，更要关注数学核心素养，引领学生走进艰难困苦的证明过程中来，最佳方法是在证明过程两旁分别书写出“基本步骤”和“数学思想与方法”，让学生深度体验问题解决的程序性和探究过程的策略性。高水平教学不仅要让学生知其然，知其所以然，还要研究“何由以知其所以然”，还学生学习主人之地位，还数学思维教育之本色。