遥感影像区域面积快速计算并行算法研究

杨静静　马骏

摘  要： 为了有效地解决遥感应用中感兴趣区域内有效遥感影像面积统计效率的问题，提出一种基于MPI（Message Passing Interface）的并行计算环境，采用经典数学定理鞋带公式（Shoelace Formula）及计算机图形学中向量积法计算多边形面积。使用三角分割法对多边形进行切割并行，判断多边形之间拓扑关系，获取交集顶点表，使用鞋带公式并行计算交多边形面积。以1.96407的加速比有效提高遥感影像有效面积统计效率，加快网页加载速度，提高用户体验度。

关键词： 遥感影像; 交多边形面积; MPI; 并行计算; 鞋带公式; 向量积

中图分类号：TP312          文献标识码：A     文章编号：1006-8228（2020）06-08-05

Abstract： In order to effectively solve the problem of statistical efficiency of effective remote sensing image area in the region of interest in remote sensing applications， this paper proposes a parallel computing environment based on MPI （Message Passing Interface）， which uses the classic mathematical theorem Shoelace Formula and Cross Product Algorithm in computer graphics to calculate the polygon area. Triangular segmentation is used to cut the polygons in parallel， determine the topological relationship between the polygons， obtain the intersection vertex data， and Shoelace Formula is used to calculate the area of the intersection polygons in parallel. With an acceleration ratio of 1.96407， it effectively improves the statistical efficiency of the effective area of remote sensing images， speeds up the loading of web pages， and improves user experience.

Key words： remote sensing image; intersection polygon area; MPI; parallel computing; Shoelace Formula; Cross Product

0 引言

隨着卫星遥感技术的迅速发展，采集的卫星遥感影像爆炸式幂指数增加。面对巨量的遥感影像，满足大范围检索条件要求的数据趋于上万条，对判断遥感影像间拓扑关系及计算遥感影像交并面积的计算效率提出挑战。

每一个遥感影像都有专属的坐标位置属性信息，故将计算多个遥感影像交并面积问题转换为计算多个简单多边形交并面积问题。计算多边形交并面积，首先需要获取多边形交并集顶点。判断任意多边形间拓扑关系不仅是计算几何与计算机图形学中的基本问题，也是GIS叠加分析的理论基础。因此，对这一问题的研究无论是在理论上，还是在实践上都有重要意义[4]。国内外针对多边形交并判断及交并面积计算问题，分别提出各类针对不同应用环境的多个多边形拓扑关系判断算法。如Shamos算法[5]、O' Rourke算法[6]用于处理凸多边形，Weiler-Atherton算法[7]、Vatti算法[8]、Greiner-Hormann算法[9]、Sutherland-Hodgman算法[10]和M.Rivero提出的算法[11]能处理任意简单多边形的情况。针对这些经典算法在不同生活领域的应用，分别存在不同角度及不同层面的不足。对此，许多相关领域专家分别提出的不同的改进方法。

齐东洲等提出优化数据结构提高算法执行效率的计算交点、将交点插入多边形顶点序列、遍历三个步骤的高效多边形布尔计算方法[12]。陈涛提出了适用于凹多边形裁剪的Cyrus-Beck改进算法[13]。刘勇奎等[14]、侯宝明等[15]和魏许青[16]等分别在Weiler算法的基础上改进算法;刘勇奎等提出的算法采用单链表数据结构，减少了计算交点的时间;魏许青利用算法中的多边形链表求出交/并集顶点表，求出交/并多边形面积;侯宝明等采用接缝技术的算法大大简化了运算过程。王结臣等提出基于扫描线和梯形分割思想的复杂多边形裁剪算法[17];彭杰等提出基于交点排序思想的多边形裁剪算法[18]等。结合以上多边形裁切算法计算多边形交/并面积的研究已经逐渐扩展。陈占龙等实现多核环境下基于Hilbert曲线空间划分的多边形并行合并[19];范俊甫等基于OGC简单要素模型和Vatti算法，在集群MPI环境下对图层级多边形叠加合并[20];赵斯思等实现基于GPU加速的多边形裁剪[21];高艺等提出基于GPU的栅格化多边形相交面积算法GPURAS，并结合蒙特卡洛方法和遮挡查询技术算法优势互补，提高计算效率[22]。上述研究学者主要在改进经典算法、经典算法结合优势互补方向深入研究，而在基于计算几何中数学定理的MPI并行环境下计算多边形交/并面积的研究较少。

本文提出了一种基于MPI并行计算环境，鞋带公式及向量积法计算多边形面积。用三角分割法对多边形进行切割并行，判断多边形之间拓扑关系，获取交集顶点表，使用鞋带公式并行计算交多边形面积的并行算法研究。本文算法在实际应用中有效提高数据执行效率，缩短程序执行时间，提高用户体验度。在遥感影像有效区域面积统计研究方面具有一定的参考价值。

1 多边形交集面积计算算法

1.1 多边形相交判断及交点坐标获取

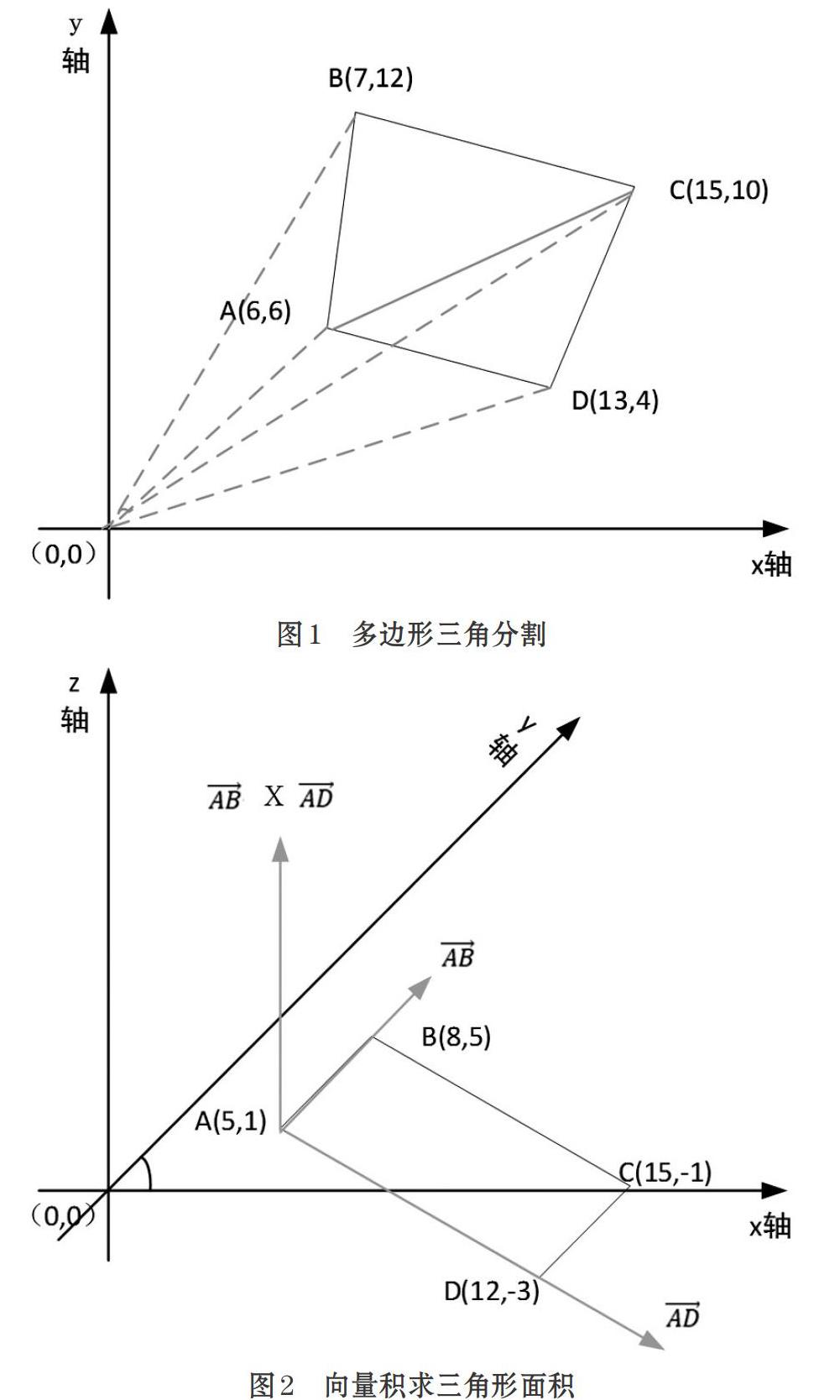
为了计算方便借坐标原点为辅助点，视多边形A为实体多边形，则多边形B为切割多边形（首先要判断多边形A、B点排列方向顺时针输入，保证多边形面积为正）。坐标原点与多边形任意相邻的两个顶点构成一个三角形（如图1多边形三角分割），而三角形的面积可由三个顶点构成的两个平面向量的外积求得。多边形面积的计算和原点的选取没有关系，通常选取原点坐标点o（0，0）或者多边形的第一个点，这里选取原点坐标点。以切割多边形B任意两点与原点o（0，0）组成的三角形ocd，每条边为直线向量切割实体多边形A任意两点与原点组成的三角形oab，用向量积法判断多边形A、B每条边之间拓扑关系，获取交点坐标集。向量积求三角形面积如图2所示。

1.2 多边形面积计算

1.2.1 鞋带公式

鞋带公式[1-3]，又称“鞋带算法”（Shoelace Formula，也称为高斯面积公式），是一种数学算法，其用于计算简单多边形的面积，这些多边形的顶点由平面中的笛卡尔坐标表示。对这些坐标进行叉乘计算，找到包围多边形的区域，并从周围的多边形中找到其中的多边形区域。根据其交叉乘的过程像系鞋带一样，故稱为鞋带公式。

1.2.2 多边形面积计算

本文用鞋带公式计算多边形面积。 依据1.1节中获取的交点坐标Pi，循环遍历鞋带算法计算两三角形有向交面积之和Sum。

传统经典算法通过循环遍历切割多边形，向量积法多次循环判断切割三角形两两之间拓扑关系判断及获取多边形交点坐标，调用鞋带算法计算交多边形面积，即计算三角形之间有向交面积并统计所有切割三角形交面积之和作为多边形有效交面积。传统多边形交面积计算程序数据计算串行执行耗时较长，在遇到多边形顶多较多的情况时会降低算法的执行效率，影响算法应用效果。

2 基于MPI并行计算交多边形面积

本文针对上述算法存在的缺陷，提出基于MPI信息传递接口并行环境计算多边形面积，对数据分块进行多线程并行计算，减少数据计算执行等待时间，提高算法的执行效率。

2.1 MPI消息传递接口

消息传递接口（Message Passing Interface，简称MPI），是一种跨语言的通讯协议，用于编写并行计算机，支持点对点和广播通信[24]。目前用于编写并行计算机较为流行。MPI是一个并行计算消息传递接口标准，由MPI论坛（MPI Forum）推出，制定该标准的目的是提高并行程序的可移植性和开发效率[25]。MPI现在已经成为产业界广泛支持的并行计算标准[26]。MPI主要消息传递接口如下。

⑴ Mpi_Init（）; 初始化MPI环境，建立多个MPI进程之间的联系，为后续通信做准备。

⑵ Mpi_Finalize（）; 退出MPI环境。

⑶ Mpi_Comm_rank（MPI_COMM_WORLD，&rank）;获取当前进程在指定通信域中的编号，返回整型的错误值，将自身与其他程序区分。MPI_COMM_WORLD类型的通信域，标识参与计算的MPI进程组;&rank返回调用进程中的标识号。

⑷ Mpi_Comm_size（MPI_COMM_WORLD，&size）;获取指定通信域的进程个数，确定自身完成任务比例。

⑸ MPI_Bcast（&n1，1，MPI_INT，0， MPI_COMM_

WORLD）;广播数据集。

⑹ MPI_Reduce（&myResult，&result，1，MPI_DOUBLE， MPI_SUM，0，MPI_COMM_WORLD）; 数据归约，由进程0进行归约，把每个进程计算出来的myResult进行相加（MPI_SUM），赋给result。

⑺ Mpi_send（buf，counter，datatype，dest，tag，comm）：buf发送缓冲区的起始地址，可以是数组或结构指针;count：非负整数，发送的数据个数;datatype：发送数据的数据类型;dest：整型，目的的进程号;tag：整型，消息标志;comm：MPI进程组所在的通信域。

⑻ Mpi_recv（buf，count，datatype，source，tag，comm，status）：source：整型，接收数据的来源，即发送数据进程的进程号; status：MPI_Status结构指针，返回状态信息。

2.2 基于MPI并行计算多边形面积

据算法使用背景本文使用组通信并行编程模型，利用消息传递方法实现任务间的并行。通过指定通信因子和组来对进程进行一种逻辑上划分，通讯因子定义了进程组内或组间通讯的上下文。Foster方法下并行化设计步骤。

⑴ 划分：数据分发，0号进程读入整个坐标数据向量，将获取的数据分为comm_size块（comm_size个核），并将数据发送给需要分量的其他进程。不同进程对收到的数据块进行计算顺序相邻的两个顶点与原点组成的三角形面积。

⑵ 通信：各线程内坐标数据块的临界坐标需要相互间通信，并发地执行对数据的相交判断及面积计算，期间多机有相互间的网络通信开销。

⑶ 聚集：多任务运行时，0号进程收集向量的所有分量，然后由0号进程聚集降低原始任务之间本需要的相互通信开销。

⑷ 映射：聚合过的任务主要通过for循环部分通过调度对任务进行并行化计算，循环中的迭代需要按照迭代次数及核数进行轮播分配。

如图3组通信任务分配所示。源数据指定特定通信组，通信组内由多个处理机组成，通信组内通过MPI_Bcast广播数据组，根据组内处理机数量对源数据进行任务分块，组内处理机之间通过网络传送消息实现相互通信，实现任务间并行。MPI_Reduce规约各个进程任务块计算结果。

本文主要用到上一节中前6个消息传递接口。

3 实验与分析

在Windows7 64位系统环境，8G运行内存，同样机型4台，一台作为主进程（0号进程，负责数据读入、分发、聚合），其他3台机作为并行节点。

实验主要采用梯度验证法设置一些测试梯度，以提高测试准确性。通常采用加速比S和效率E来测量并行计算效率，如等式⑸和等式⑹。

其中，Ts为串行算法执行耗费时间，Tp为并行算法执行耗费时间，P为算法并行节点数。

为了更加准确的验证实验结论，本文分两种情况进行实验验证，一是节点数一定改变多边形顶点数;二是多边形顶点数一定改变节点数。首先我们验证节点数一定为2，多边形顶点数分别为3，10，20，40，实验结果如表1节点数一定改变多边形顶点个数和图4节点数一定改变多边形顶点个数所示。

当并行节点数一定时，改变串行、并行顶点数量，发现随着顶点数的增加计算时间增大，当数据过小时CPU消费的时间会影响并行计算效率，并行效果不明显，在顶点数一定时串行和并行计算时加速比和效率是呈线性增加趋势。

再次验证顶点数一定为20，节点数分别为1，2，3，4，实验结果如表2多边形顶点个数一定改变节点数和图5多边形顶点个数一定改变节点数所示。

当顶点数一定时，改变并行节点数量，发现随着节点数的增加，计算时间增大，当数据过小时，CPU消费的时间会影响并行计算效率。节点数继续增加，加速比增长缓慢且有下降趋势，因为线程启动需要开销一定的时间。故随着节点数的增加，并行程序的效率越来越低。

综上所述，本研究中当节点数为2时，并行计算效率最高，达到相对最佳并行计算节点。

4 结论

本研究主要为了解决多边形顶点足够多时，多边形分割及三角形向量面积计算需要通过多层循环遍历，程序串行执行效率低下问题。本文提出基于MPI并行计算多边形交面积，提高多边形面积计算效率。在多边形顶点增多时，本文并行计算多边形面积效率明显比串行计算速度快，相比串行方法本文并行计算方法在提高计算效率方面具有一定的研究价值。但是本文实验利用消息传递方法实现多处理机处理任务并行，该方法需要网络环境才能实现多处理机的并行，本次实验仅在一种网络环境下进行实验，接下来可以尝试换一种网络带宽进行并行测试，来验证并行实验的有效性。

参考文献（References）：

[1] Dahlke， Karl. "Shoelace Formula" （http：//www.mathreference.com/la-det，shoe.html）. Retrieved 9 June 2008.

[2] Shoelace Theorem （http：//www.artofproblemsolving.com/wiki/index.php？title=Shoelace_Theorem）， Art of Problem Solving Wiki.

[3] Younhee Lee，  Woong Lim. Shoelace Formula： Connecting the Area of a Polygon with Vector Cross Product[J]. The Mathematics Teacher，2017.110（8）：631-636

[4] 朱雅音，王化文，萬丰等. 确定两个任意简单多边形交_并_差的算法[J]. 计算机研究与发展， 2003.4：69-76

[5] Preparata. Computational Geometry： An Introduction[J]. texts & monographs in computer science，1986.47（176）.

[6] O' Rourke. Computational Geometry in C[J]. Cambridge：Cam-bridge University Press，1985.37：128-129

[7] Kevin Weiler ， Peter Atherton. Hidden surface removal using polygon area sorting[C]. Proceedings of the 4th Annual Conference on Computer Graphic and Interactive Techniques，1977.11：214-222

[8] Bala R. Vatti.  A generic solution to polygon clipping[J]. Communication of the ACM，1992.35：56-63

[9] Hoffmann CM ， The problems of accuracy and robustness in geometric computations[J]. IEEE Computer，1989.22：31-42

[10] 苏诚，韩俊刚.Sutherland-Hodgman裁剪算法的改进[J].西安邮电学院学报，2013.18（3）：80-82

[11] Rivero， F R Feito. Boolean operations on general planarpolygons[M].Computers& Graphics，2000.24（6）：881-898

[12] 齊东洲，吴敏.高效的多边形布尔计算方法[J].计算机应用，2014.S2：85-89

[13] 陈涛.适用于凹多边形的Cyrus-Beck改进算法[J].计算机科学，2006.33（12）：217-220

[14] 刘永奎，高云，黄有群.一个有效的多边形裁剪算法[J].软件学报，2003.14（4）：845-856

[15] 侯宝明，刘雪娜.任意多边形区域交的有效算法[J]，计算机辅助工程，2009.18（2）：73-76

[16] 魏许青.计算多边形交集_并集面积的算法[J].计算机工程与科学，2007.12：89-90

[17] 王结臣，沈定涛，陈焱明，等.一种有效的复杂多边形裁剪算法[J].武汉大学学报（信息科学版），2010.35（3）：369-372

[18] 彭杰，刘南，唐远彬等.一种基于交点排序的高效多边形裁剪算法[J].浙江大学学报（理学版），2012.39（1）：107-111

[19] 陈占龙，吴亮，刘焕焕.多核环境下Hilbert曲线划分简单要素多边形合并算法[J].计算机应用研究，2012.29（7）：2747-2750

[20] 范俊甫，马廷，周成虎等.基于集群MPI的图层级多边形并行合并算法[J].地球信息科学学报，2014.16（4）： 15-21

[21] 赵斯思，周成虎.GPU加速的多边形叠加分析[J]. 地理科学进展，2013.32（1）：114-120

[22] 高艺，罗健欣，裘杭萍等.基于GPU的任意多边形相交面积计算方法_高艺[J].测绘工程，2017.26（12）：58-62

[23] Meister， A. L. F.， Generalia de genesi figurarum planarumet inde pendentibus earum affectionibus， https：//books.google.com/books？id=fOE_AAAAcAAJ，1769，Nov.Com. G?tt. （in Latin）， 1：144

[24] https：//baike.baidu.com/item/MPI/15277241？fr=aladdin

[25] 李久楷，朱俊，宁交贤.MPI并行计算性能的研究[J].四川大学学报（自然科学版），2009.33（5）：496-499

[26] 申焕，石晓春，邱宏华.基于MPI的海量遥感影像并行处理技术探析[J].全球定位系统，2012.37（6）：73-76