东露天煤矿槽仓三维有限元变形分析

杨 喆，晁 军

(中煤西安设计工程公司，陕西 西安 710054)

随着我国基础设施的快速发展，越来越多的工程都面临着深基坑的问题。常用的研究方法主要有：理论方法、试验方法、数值法、理论与实际量测相结合的方法等。因数值方法较传统方法有许多优势，已成为现今比较流行的方法。国内外学者也对其进行了大量研究。如杜东宁等[1]、张玥[2]、朱建新[3]等采用有限元方法对深基坑开挖过程进行了仿真分析。孟文清等[4]、郭力等[5]、韩健勇等[6]采用数值分析法对深基坑围护结构受力变形及稳定性进行了分析。李四维等[7]、霍润科等[8]采用有限元与现场监测相结合的方法进行了深基坑开挖的变形分析。但是，当前大部分的研究主要是针对高层、地铁等形状较为规则，面积较小，支护结构较为单一的深基坑进行的。

目前，对于大型槽仓，由于基坑支护深度大，结构受限制，仓壁坡度陡，变形控制要求高，有限元网格数目接近100万单元，鲜见利用商用软件进行三维计算，商业软件也无法计算这样大的规模，三维并行计算更是未见先例。本次山西平朔东露天煤矿槽仓的有限元计算，基于弹塑性模型进行三维并行有限元力学分析[9，10]，散粒体计算采用了颗粒离散元算法[11，12]，共86.5万单元，在曙光并行机上，利用40个节点即40个CPU进行并行计算，每个方案计算25min左右。尤其是三维并行有限元算法和散粒体离散元算法，具有理论上的开创性，应用于目前国内最大规模的储煤槽仓具有示范意义，因此该项目具有理论和应用的双重意义。

1 工程概况及地质条件

1.1 工程概况

平朔东露天煤矿选煤厂位于山西省朔州市，2009年1月5日开工建设。槽仓设计储量为20万t，服务年限80a，为目前国内最大规模的储煤槽仓。槽仓长237.0m，上口宽38.3m，下口宽16.0m，深30.4m，仓壁坡度为60°，槽底布置有高7.7m，宽16.0m的钢筋混凝土输煤暗道，暗道上部布置有3个钢筋混凝土落煤筒。仓体左侧设备端开挖深31.2m，右侧出口端深44.0m，其中上部32.6～35.0m为填方形成，下部8.4～14.0m开挖形成。槽仓纵向板件跨度2.5～3.0m，最大变形缝间距20mm，基础底板厚40mm，混凝土强度等级C40，抗渗等级S12，能储容重为：1×10-5N/mm3，休止角为38°的煤约20万t。

槽仓位于黄土地层，仓底位于地下水位以下，地层含有红土软弱夹层。在场地内存在一走向北东—南西向的基岩陡坎面，基岩陡坎面以西基岩埋深较浅，以东基岩埋深较深，而基岩变化与天然斜坡坡形变化趋势一致，故仓体分为挖方段和填方段两部分，挖填方分界线为基岩面变化的分界线[13-16]。

1.2 地质条件

根据钻孔揭露情况，场地地层自上而下主要有[17]：

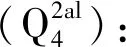
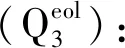
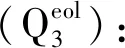
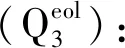
⑦强风化泥岩(P1x)：灰色-黄灰色，泥质胶结，具薄层水平层理，上部风化裂隙发育，岩体破碎，风化后松散，遇水崩解，塑性较强，在该层中发育有NE及NW两组节理裂隙。

2 模型的建立

对于槽仓这种复杂和大型的问题没有现成的商用软件，而PFEPG[18]是当前国内外唯一的并行有限元程序自动生成系统，本项目以PFEPG为开发和计算平台，采用新的软件开发模式，保证了槽仓大型三维有限元计算问题能够在短期内完成。

为了保证有限元分析的精度和适应槽仓的模型，首先将整个复杂的槽仓模型划分为很多简单的子区域，将计算区域边界上地层网格底部固定，作为参考计算平面，地层周边边界作为无穷远边界处理；黄土地层等土体采用八节点六面体实体单元模拟，根据固体力学弹性及塑性理论选用适当物理本构模型。钢筋混凝土部分，如落煤筒、仓下暗道、两侧建筑挡墙等结构，也采用实体单元模拟，采用小变形弹性力学及塑性力学理论分析；锚杆、锚索、土钉等支护，由于使用方式为批量系统使用，故而采用等效刚度方法模拟，其中锚杆采用全程铰接的小变形小应变杆单元理论模型，选用线弹性本构模型；锚索采用两端铰接中间非协调变形的杆单元理论模型，小变形小应变线弹性本构模型；土钉采用与土体协调变形的杆单元理论模型，计算本构模型为线弹性模型。

挖方段在地应力平衡的基础上，做一次性开挖处理，采用岩土弹性塑性模型卸载。为减少程序编写的工作量，卸载过程和填方过程采用同一计算本构模型。槽仓的开挖和填筑过程采用准静态模型分四步模拟，黄土的开挖与支护效果则采用死活单元模拟。

最终依据工程地质资料采用图形建模软件GID建立计算几何模型如图1所示。

图1 有限元模型

3 三维数值模拟结果与分析

在计算中，开挖与回填均分四步完成，每一步开挖都是在前一步计算的基础上进行，初始地应力下的位移变形与应力分布情况如图2—图5所示。

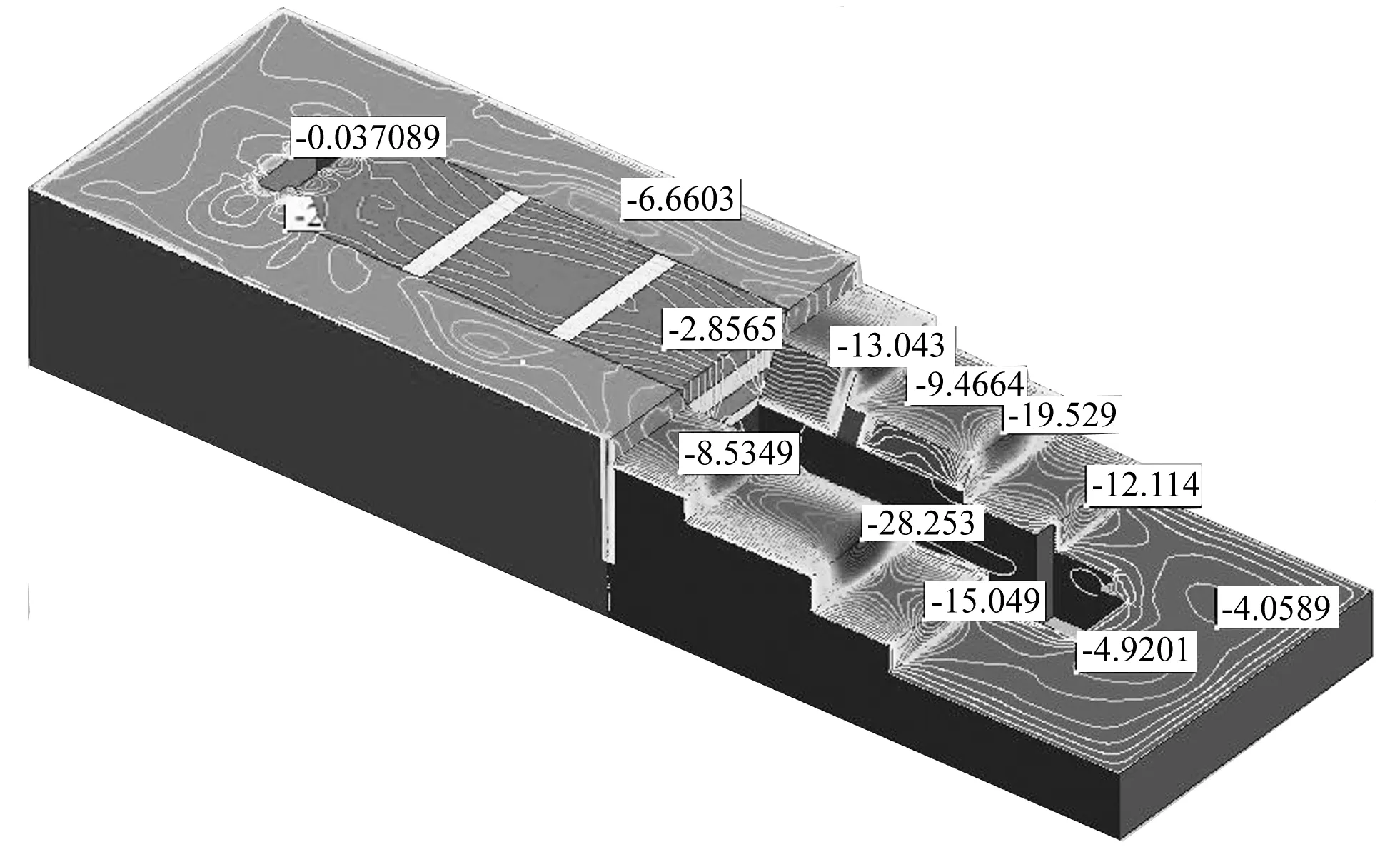
图2 初始地应力下重力方向变形等值线图

图3 初始地应力下南北水平方向变形等值线图

图4 初始地应力下重力方向横剖面处变形等值线图

图5 初始地应力下南北方向横剖面处变形等值线图

重力方向整体变形发生在-28.253mm到12.745mm之间，而南北水平方向的变形发生在-11.294到11.836mm之间。整体上看，初始网格变形量不大。

3.1 挖方段计算结果

限于篇幅，本文仅给出了最后一步即第4步开挖结束时开挖区重力方向和南北水平方向变形等值线，如图6、图7所示。

图6 第四次开挖区重力方向变形等值线图

图7 第四次开挖区南北水平方向变形等值线图

由图6、图7可知，开挖区竖向变形为正，表示地层开挖后基础向上反弹。在本次分析计算中考虑施工过程与工序的影响，开挖分四次完成。每次开挖后，开挖边坡向临空面方向回弹，槽仓两侧壁处变形稍大，表示边坡变形，两侧壁上部塌缩下部突出，最大回弹位移位于暗道底部。整体变形上为滑动趋势。槽仓外侧支护桩顶部临时支护梁与暗道顶部横梁有效抑制了边坡水平位移，起到了加固的关键作用。

每次开挖后，地层会有少量向上反弹。从计算结果中可知开挖区背离落煤筒的地方向上反弹幅度更大，而靠近落煤筒处开挖过程中变形则相对较小。此外，历次开挖结果图表明，挖方区边坡开挖过程中，边坡向临空面方向滑移，开挖到设计边坡坡脚时，最大位移位于边坡坡脚处；继续开挖，最大位移处即向下转移，集中在外侧支护桩与左侧护壁桩之间。在南北方向的水平其变形幅值不超过为3.5cm，相对整个模型的尺度来说，不易发生边坡滑塌问题，由于不考虑地层暴露力学性质的改变，整体开挖区域有少量回弹，与建筑物接触处变形量可不计。

槽仓开挖加固后，应力场发生重新分布，塑性区位于槽仓暗道底部、暗道顶梁与外侧支护桩之间、边坡坡脚与外侧支护桩连接处附件，这些地方是支护设计的重点加固部位，应引起高度重视。

3.2 填方段计算结果

限于篇幅，本文仅给出了最后一步(第4步)回填结束时回填区重力方向和南北水平方向变形等值线，如图8—图11所示。

图8 第四次回填后重力方向变形图

图9 第四次回填后南北水平方向变形图

图10 第四次回填后重力方向横剖面处变形图

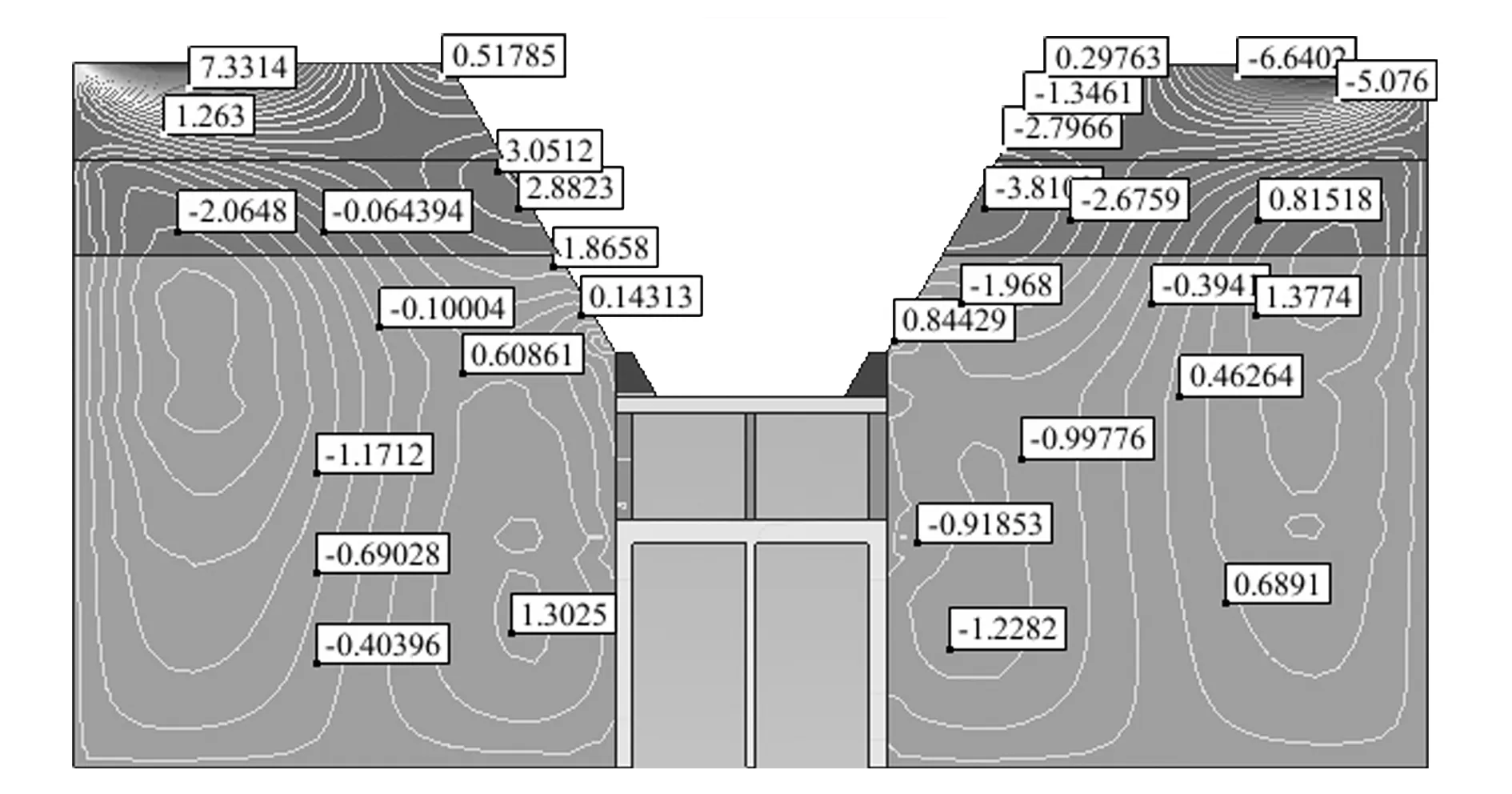
图11 第四次回填后南北水平方向横剖面处变形图

由图8—图11可知，填方区边坡施工过程中，每次回填都认为是在前次回填稳定的基础上进行，只计算本次回填的沉降和荷载增量对前面回填底层的影响。从历次回填的计算结果看，随着填方一层一层固结完毕，水平位移和竖向位移均逐渐增大，但发生的变形主要以重力方向的变形为主，较大的垂直变形主要发生在靠近边坡朝里的一侧，坡脚与暗道左侧护壁桩底部出现应力集中，并表现出较大水平位移。但每次回填的最大下沉量在5～7cm之间，边坡在南北水平方向的变形也相对较小，变形幅值不超过1.5cm。

此外在回填过程中，边坡表层出现部分塑性区域，表明边坡表层土体可能会出现浅层滑动，需要进行表层土体的加固防护。回填土与原状土连接段及回填土底层部分亦出现塑性区，表明施工中在该区域需做好不同土质的压实衔接。

4 与实测结果比较

为了进一步说明三维并行有限元计算方法的准确性，本文将数值计算结果和现场实际监测数据进行了比较，对比结果见表1。

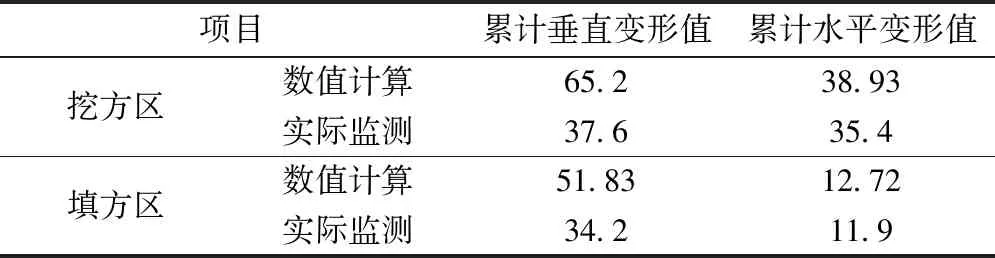
表1 数值模拟与实际监测值结果比较 mm

通过计算数据与监测数据的比较，槽仓最终累计垂直和水平变形值均较实际监测数据值大。其中水平变形值相差较小，误差率仅6.89%～9.97%；垂直变形值相差虽较大，但总体趋势基本相同，均满足工程需要。

此外，监测数据反映槽仓的水平变形值较小，说明整个槽仓在施工期间是稳定可靠的，没有发现任何异常突变，也说明槽仓在开挖期间在一定程度上没有引起水平位移的变化。而槽仓的垂直变形值较大，说明槽仓的开挖对垂直位移监测点有一定影响，但这种影响在安全范围之内。

5 结 论

1)利用有限元法进行槽仓开挖回填过程的数值模拟研究是切实可行的，模拟分析得到的数值结果满足工程以及理论上的基本要求，与实际工程测量结果大致吻合。

2)基于数值模拟结果，开挖段每次开挖后，地层会有少量向上反弹。当第四次完成后，槽仓两侧壁处变形稍大，表示边坡变形，两侧壁上部塌缩下部突出，整体变形上为滑动趋势。此外，挖方区边坡开挖过程中，在南北方向的水平变形幅值不超过为3.5cm，满足工程需要。

3)基于数值模拟结果，回填段每次回填后，发生的变形主要为重力方向的变形，南北水平方向的变形相对较小，较大的垂直变形主要发生在靠近边坡朝里的一侧，每次回填的最大下沉量在5～7cm之间。南北水平方向的变形幅值不超过1.5cm，满足工程需要。

4)开挖回填完成后，槽仓结构的最大变形发生在槽仓东侧提升间结构的上端和下端。在上端变形显示为向外膨胀，而在下端为对内挤压，不过整体来看变形幅度均不大，最大变形1.7cm左右，满足工程需要。