对称式、交代式、齐次式、轮换式在初中数学中的应用

杨龙田

(安徽省合肥市新东方外语培训学校 230000)

一、基础概念说明

1.对称式

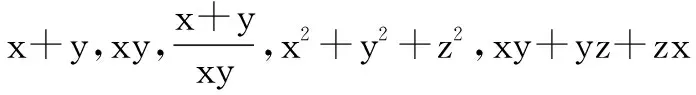
2.齐次式

一个n元多项式的各项的次数均等于同一个常数r，那么称这个多项式为n元r次齐次多项式.例如，

含三个字母的三元一次齐对称式为：A(x+y+z)；

含三个字母的三元二次齐对称式为：A(x2+y2+z2)+b(xy+yz+zx)；

含三个字母的三元三次齐对称式为：

a(x3+y3+z3)+b(x2y+x2z+y2x+y2z+z2x+z2y)+cxyz.

3.交代式(多见于因式分解)

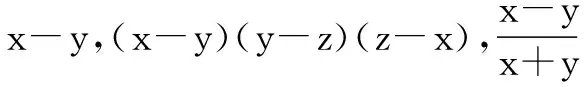
4.轮换式

一个多项式含有x、y、z，如果用x替换y，y替换z，z替换x，得到的代数式与原来的代数式还相等，那么称这个代数式为轮换对称式，简称轮换式.显然，对称式一定是轮换式，但轮换式不一定是对称式.例如，a(x2+y2+z2)是对称式也是轮换式；b(x2y+y2z+z2x)是轮换式，但不是对称式.

二、运用示例

对称式、交代式、齐次式、轮换式在初中数学中的应用主要是涉及整式乘法、因式分解、分式这三个模块.掌握对称式、交代式、齐次式、轮换式在七年级数学中的整式乘法、因式分解、分式，使得解这类题更加简便.在有关不等式中的应用属于较高要求.

1.在整式乘法中的运用

例1计算：(a+b+c)3.

分析(a+b+c)3是一个三次齐次的对称式，则展开式是含字母a ，b ，c的三次齐次的对称式，其同型式的系数相等，可用待定系数法.

解设(a+b+c)3=m(a3+b3+c3)+n(a2b+a2c+b2c+b2a+c2a+c2b)+pabc(m、n、p是待定系数).

令a=1,b=0,c=0.比较左右两边系数得m=1；

令a=1,b=1,c=0比较左右两边系数得2m+2n=8；

令a=1,b=1,c=1比较左右两边系数得3m+6n+p=27.

点评这道题如果使用整式乘法法则计算，会比较复杂，但是在掌握了齐次式的概念，就能知道该式子展开是什么类型，不能确定的就是系数，因此利用待定系数法，就可快速求得结果.

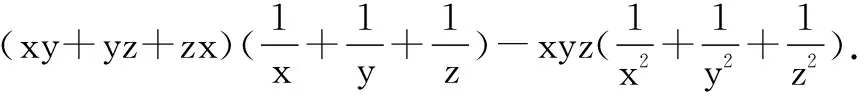
点评两个对称式(轮换式)的和，差，积，商(除式不为零)，仍然是对称式(轮换式).

2.在因式分解中的运用

基本规律：两个对称式(轮换式)的和，差，积，商(除式不为零)，仍然是对称式(轮换式).故：轮换式的因式分解结果仍是轮换式，交代式的因式分解结果一般是交代式和轮换式的乘积.交代式一般仅在因式分解当中有所考察.

例3分解因式：(b-c)3+(c-a)3+(a-b)3.

分析原式多项式是轮换式，则因式分解的结果还是一个轮换式.利用因式定理可发现，当a=b时，多项式值为零，因此，分解过后的式子肯定含有a-b，则同时含有b-c和c-a，这时候只要确定系数即可.

解设(b-c)3+(c-a)3+(a-b)3=k(a-b)(b-c)(c-a),令a=2,b=1,c=a得k=3.故：(b-c)3+(c-a)3+(a-b)3=3(a-b)(b-c)(c-a).

点评这道题关键点是运用因式定理，但是对称式、交代式、齐次式、轮换式的知识会在当中起到辅助的作用.另外，要注意的是，这道题分解的结果并不是简单的(a-b)(b-c)(c-a)相乘，前面还有系数.

变式因式分解：a3(b-c)+b3(c-a)+c3(a-b).

解∵当a=b时，a3(b-c)+b3(c-a)+c3(a-b)=0,

∴有因式a-b及其同型式b-c,c-a.

∵原式是四次齐次轮换式，除以三次齐次轮换式(a-b)(b-c)(c-a)，可得一次齐次的轮换式a+b+c.用待定系数法：得a3(b-c)+b3(c-a)+c3(a-b)=-(a+b+c)(a-b)(b-c)(c-a).

例4 因式分解：x3-y3.

分析x3-y3是一个三次齐次交代式，则因式分解的结果是奇数个交代式与若干个对称式相乘.而利用因式定理可知，x3-y3因式分解的结果含有一个x-y，剩下的就是一个二次对称式了，设该二次对称式为m(x2+y2)=kxy，易知m=1，只要确定k即可.

解设x3-y3=(x-y)(x2+kxy+y2),当x=1,y=-1时，解得k=1,故x3-y3=(x-y)(x2+xy+y2).

点评x3-y3是一个交代式，则x3-y3的分解结果会含有交代式和轮换式，当x=y时，原代数式为0，故x3-y3含有因式x-y，这个刚好是交代式，剩下一个次数是2的轮换式.

例5 因式分解：x3+y3+z3-3xyz.

分析x3+y3+z3-3xyz是一个对称式，当x+y+z=0时，原式为0，故x3+y3+z3-3xyz因式分解含有x+y+z，而x3+y3+z3是一个三次齐次轮换式，则分解后剩下的部分是二次齐次轮换式，可设为：A(x2+y2+z2)+B(xy+yz+zx).

解x3+y3+z3-3xyz=(x+y+z)[A(x2+y2+z2)+B(xy+yz+zx)]，利用待定系数法求得A=1，B=-1.故x3+y3+z3-3xyz=(x+y+z)(x2+y2+z2-xy-yz-zx).

点评一次齐次的轮换式形如：A(x+y+z)，二次齐次的轮换式形如：A(x2+y2+z2)+B(xy+yz+zx).

3.在分式中的运用

对称式、交代式、齐次式、轮换式在此模块中的核心解题技巧是：

(1)若含有x、y、z的代数式是对称式，则在解题中可设x≤y≤z；

(2)若含有x、y、z的代数式是轮换式，且x，y满足性质p，则x，z；y，z也满足性质p；

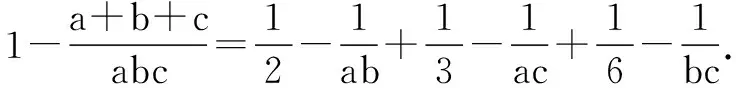
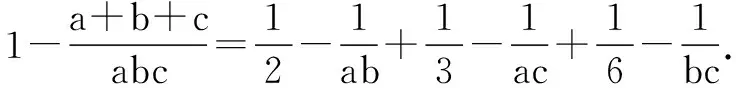
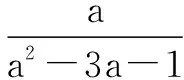
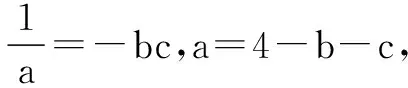
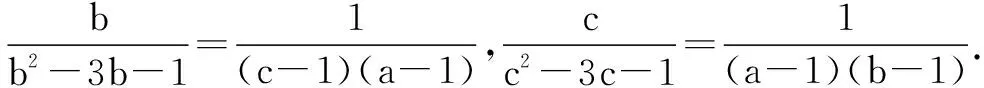
所以：(a-1)(b-1)(c-1)=abc-(ab+bc+ca)+(a+b+c)-1=1,得:ab+bc+ca=1,所以：a2+b2+c2=(a+b+c)2-2(ab+bc+ca)=14.

点评这道题难度大，对称式、交代式、齐次式、轮换式的存在提供了一个解题方向：对三个式子进行相同的处理.这就是对称式、交代式、齐次式、轮换式存在的意义.

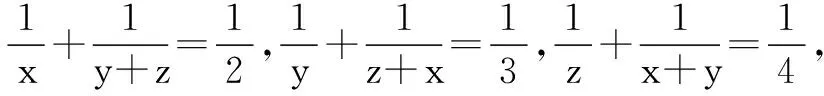
分析这道题条件中的代数式是三个轮换式，而且条件是三个等式，这里处理的方式即是对三个等式进行相同的变化.

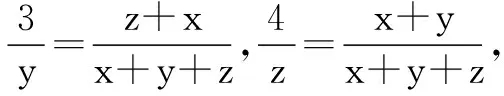
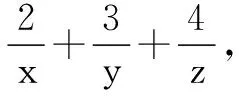
分析典型的轮换式，对条件的三个式子同时取倒数即可.

点评此题对于条件的变化方式还是相同：取倒数.变化后的式子依然是相加得到所需结果.

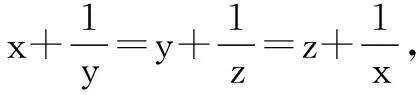
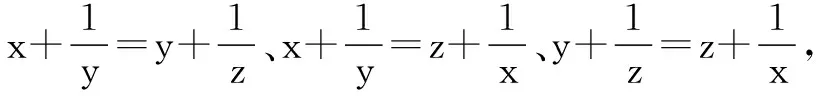
三式相乘得：x2y2z2=1,故xyz=±1.

点评此题条件是连等式，解决方式则是将连等式转化成三个等式.前提条件是准备认识到题目条件给出的是轮换式.难点在于三个等式的变化方式.因此，在理解“轮换式”的基础上，还是要进行一些尝试，才能得到最终的解题方式.

4.在有关不等式中的应用

例11 (2019高考数学全国1卷第23题[选修4-5：不等式选讲])已知a、b、c为正数，且满足abc=1.证明：

(2)(a+b)3+(b+c)3+(c+a)3≥24.

分析第(1)问是一个明显的对称式，第二问是一个明显的轮换式.第一问只要将分子1换成abc，然后移项配方就可以做出来；第2问要用到均值不等式.

⟸a2+b2+c2-ab-ac-bc≥0

点评对称式、交代式、齐次式、轮换式给出了一些解题方向，第1问处理方式，第二问部分处理方式.但是重要的还是课内的基础知识，对称式、交代式、齐次式、轮换式能算得上“锦上添花”.第2问要用到均值不等式的延伸：a3+b3+c3≥3abc.

以上例题还存在片面性，对称式、交代式、齐次式、轮换式一般出现在竞赛相关的知识当中，学习这个可以锻炼思维，能够学会从不同角度解决问题，提升思维能力、解题能力.