矩阵的核-EP分解及其应用

朱光辉，左可正，蒋万林

(湖北师范大学 数学与统计学院，湖北 黄石 435002)

0 引言

下面给出本文中需要的一些广义逆。

定义1[1]设矩阵,考虑矩阵方程:

1)AXA=A2)XAX=X3)(AX*)=AX4)(XA)*=XA

矩阵X∈n×m满足方程(1),称X为A的{1}-逆,记作A-.存在唯一的矩阵X∈n×m满足矩阵方程1)、2)、3)、4),称X为A的M-P逆,记作A+.

定义2[2]设矩阵A∈n×n,则存在唯一的矩阵X∈n×n满足:

1)AXA=A2)XAX=X3)AX=XA

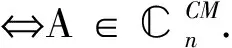
矩阵核-EP逆是矩阵的一种重要广义逆。Manjunatha和Mohana在文献[3]中首次给出了核-EP逆的定义及其性质。核-EP逆是核逆的推广,下面给出核-EP逆的定义。

定义3[3]设矩阵A∈n×n,ind(A)=k,则存在唯一的矩阵X∈n×n满足:

1)XAX=X2)R(X)=R(X*)=R(Ak)

称X为A的核-EP逆,记作A⊕.

定义4[4,5]设矩阵A∈n×n,L是n的子空间,若APL+PL⊥是可逆矩阵,则A关于子空间L的Bott-Duffin逆记为且

利用矩阵分解来研究矩阵的性质,是矩阵分析的一种重要方法。本文首先运用Schur分解定理给出了核-EP分解定理的一个新证明；而后运用矩阵的Bott-Duffin逆及核-EP分解定理给出了A的核-EP逆A⊕的新刻画。

引理1[1](Schur引理)设A∈n×n,则A酉相似于一个上三角矩阵,且该矩阵的主对角线元素为矩阵A的特征值。

引理2[6]设A∈n×n,A关于子空间L的Bott-Duffin逆记为则有:

且APL+PL⊥可逆⟺r(PLAPL)=r(PL)=dim(L)

定理1 设设A∈n×n,ind(A)=k,则其中可逆，Nk=0)

证明 由引理1知对任意矩阵A∈n×n,A酉相似于一个上三角矩阵,即存在一个酉矩阵U使得

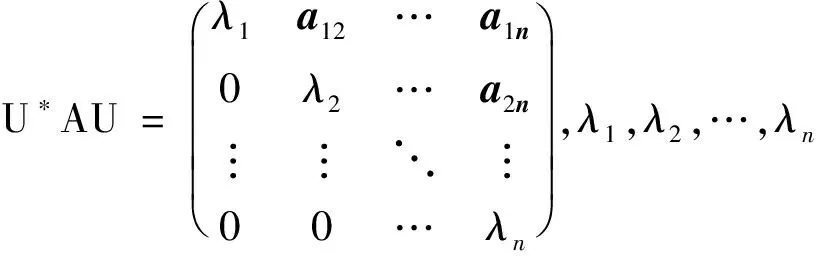
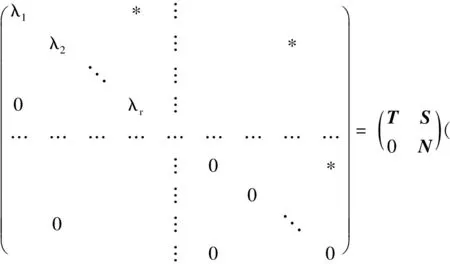
1 核-EP分解定理的一个新证明

核-EP分解定理是研究矩阵A的核-EP逆A⊕的一个重要工具。在文献[6]中王宏兴给出了核-EP分解定理,并利用Schur分解定理证明了核-EP分解定理。下面我们利用A的M-P逆A†给出了核-EP分解定理的一个新证明。

定理2[6](核-EP分解定理)

设A∈n×n,ind(A)=k,则存在唯一的A1∈n×n,A2∈n×n,使得A=A1+A2,且有:

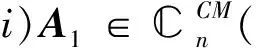
此时称A1为A的核-EP分解的核部分,A2为A的核-EP分解的幂零部分。

证明 先证分解的存在性。

i)令A1=Ak(Ak)†A,A2=A-A1,A=A1+A2,

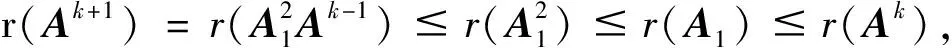
从而A2A1=(A-Ak(Ak)†A)Ak(Ak)†A)=Ak+1(Ak))†A-Ak-1(Ak)†A=0；

通过归纳证明可得出

这样就证明了核-EP分解的存在性。

下证分解的唯一性。

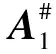
由核-EP分解定义可得

(1)

等式(1)两边同时乘以A1及结合A2A1=0可得出

(2)

(3)

综合等式(1)(3)可得r(Ak)≤r(A1)≤r(Ak),所以r(A1)=r(Ak).

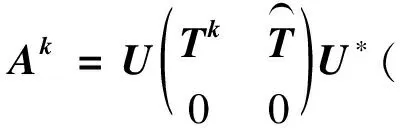
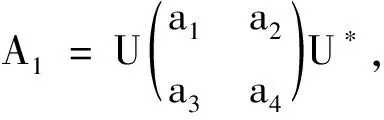
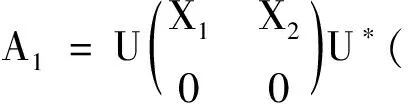
r(A1)=r(X1X2)=t, ,所以矩阵(X1X2)是行满秩矩阵，从而(X1X2)是右可逆矩阵，设

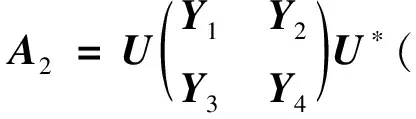
由A2A1=0通过计算可得出

Y1X1=0,Y1X2=0,Y3X1=0,即Y1(X1X2)=0,Y3(X1X2)=0,所以Y1=0,Y3=0.

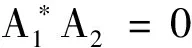
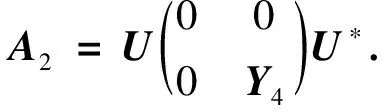
所以X1=T,X2=S,Y4=N.

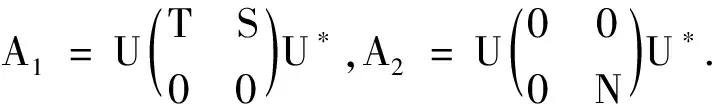
综上所述,定理得证。

2 A⊕的表达式及其特征

核-EP逆A⊕是矩阵的一类重要广义逆,文献[3]给出了核-EP逆A⊕的一个刻画A⊕=Ak((A*)kAk+1)-(A*)k.文献[6]运用核-EP分解定理给出了等式AA⊕=Ak(Ak)†及A⊕的一个刻画A⊕=Ak((A*)kAk-1)†Ak.文献[8]给出了A⊕的一个刻画A⊕=(APAk)†.文献[9]给出了核-EP逆的一些等价条件。

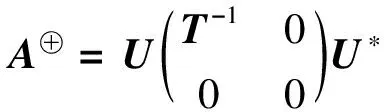
定理3[9]设A∈n×n,则

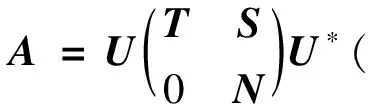
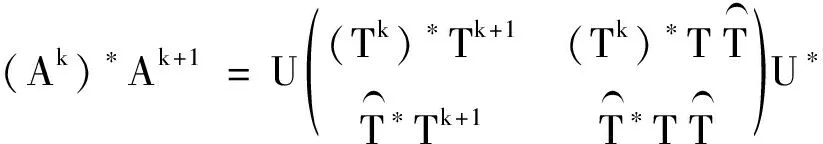
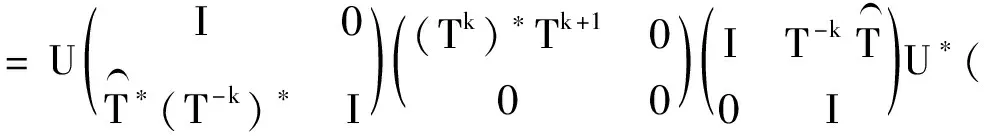
由此得出

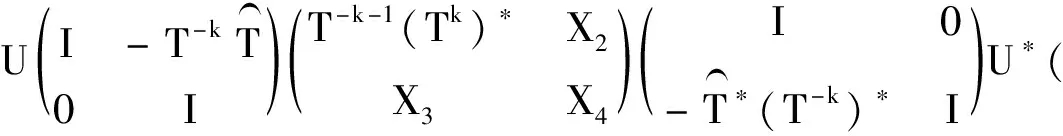
定理4 设A∈n×n,ind(A)=k,则

证明 因为r(Ak)=r(Ak+1(Ak)†Ak)≤r(PR(Ak)APR(Ak))=r(Ak+1(Ak)†)≤r(Ak(Ak)†)=r(Ak),

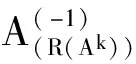
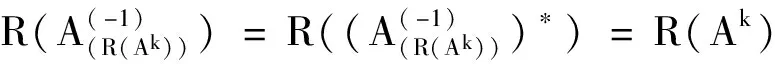
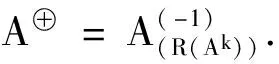
注记 运用定理4和定理1可以给出定理3的另一种证明方法。