基于灰色关联度法和强度折减法的边坡稳定性影响因素敏感性分析

黄盛锋，陈志波，郑道哲

(1.福州大学环境与资源学院岩土与地质工程系，福建 福州 350116；2.自然资源部丘陵山地地质灾害防治 重点实验室，福建 福州 350116；3.地质工程福建省高校工程研究中心，福建 福州 350116)

0 引言

边坡的稳定性分析一直以来是边坡工程中一个重要的工作[1]，边坡失稳将造成难以想象的后果。目前，对于边坡稳定性分析，岩土工程界主要应用极限平衡条分法和有限元法。但极限平衡法自身的缺陷，需要在计算之前假设边坡的滑动面的位置，但假设常与实际不符产生误差。强度折减法(SRM)能直接求解安全系数，并通过后处理得出相应的滑动面，对于复杂的地质条件有较好的适用性，因此得到了普遍的应用。但其缺点同样明显，SRM采用单一折减系数，默认c、φ在边坡滑动过程中起着相同的作用，而容易引起误差。

针对SRM的缺陷，唐芬等[2]在条分法的基础上，提出了强度参数在两个不同折减参数下的双强度折减法(DRM)的概念，研究了两个不同折减系数的相关性，认为c、φ在边坡失稳过程中有着不同程度的贡献。但边坡失稳是一个十分复杂的过程，定量计算的参数在获取时都具有不确定性、模糊性和随机性等特点[3]，c、φ如何折减还很难确定。唐芬等[4]提出土坡渐进破坏的双折减系数法，通过不断改变黏聚力折减系数与内摩擦角折减系数间的关系来研究黏聚力折减速率与内摩擦角折减速率之间的关系。JIANG X Y等[5]指出各向同性的土质边坡中黏聚力折减系数与内摩擦角折减系数之间的比例应为1.75∶1。但上述两位学者的研究都没有明确两个折减系数之间的关系，且对于φ、c、μ、Ф、E的影响程度、有没有必要对弹性模量E、泊松比μ以及剪胀角Ф进行折减还没有定论，因此本文对SRM中使用的参数进行敏感性分析，分析φ、c、μ、Ф、E在边坡失稳过程的影响程度，为上述问题提供参考。

目前，边坡稳定性敏感性分析所采用的方法主要有：正交设计法[6]、均匀设计法[7]、人工神经网络分析法[8]、灰色关联度法[9]等。但鲜有人在强度折减法中应用这些方法，本文将基于灰色关联度法，进行强度折减法边坡稳定性敏感性分析，分析φ、c、μ、Ф、E的影响程度和内在联系，并通过ABAQUS有限元软件分析上述影响因素对滑动面的影响，为双强度折减法提供参考，并提出改进建议。

1 灰色关联度法基本原理

灰色关联分析由邓聚龙教授[10]提出，是一种不确定性分析方法。通过计算目标因素与对应因素之间的主要关系，找出对目标因素影响程度最大的因子，通过量化它们之间的关系程度，定量说明变化因素与对应因素之间的相互联系。

1.1 确定序列矩阵

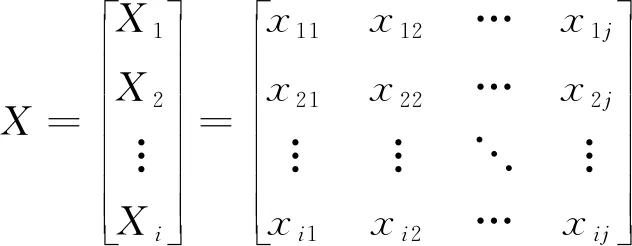
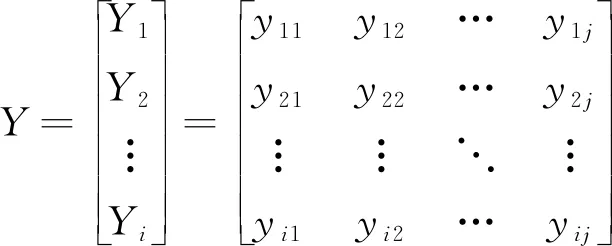
选取边坡的参数φ、c、μ、Ф以及E为影响因子子序列X，对应的边坡稳定性系数作为母序列Y。对每个X取若干个值，则Y也将相应的得到若干个值，可得X、Y的矩阵形式为：

(1)

(2)

式中：xij——表示第i个因子的第j个取值；

yij——表示对应第i个因子第j个变化值的边坡稳定性系数。

1.2 矩阵的无量纲化、差异序列矩阵的确定

由于各影响要素的量纲不同，并且数值差异性较大，不便于直接进行比较，因此要对母序列和子序列中各因素进行变化。矩阵的无量纲化方法有：初值化、均值化、区间相对值化和归一化等[9]。本文用区间相对值化，即：

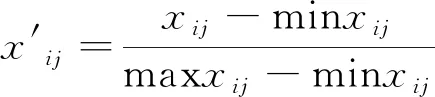
(3)

对母序列Y做同样处理，即可将影响因素和边坡稳定性系数无量纲化。

将无量纲化的子序列与母序列进行如下处理，得到差异序列矩阵Δ，并取出其中的最大值和最小值：

Δij=|x′ij-y′ij|

(4)

Δmax=maxΔij

(5)

Δmin=minΔij

(6)

1.3 关联系数矩阵与关联度

关联系数矩阵L中各因子采用下式计算：

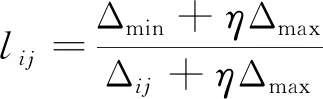
(7)

式中：η——为分辨系数，一般取η=0.5。

求取关联度：

(8)

取值范围为(0,1)，与对于边坡稳定性系数的影响程度成正比。

2 基本算例与参数选取

2.1 基本算例概况

下文基于DAWSON等[11]均质土坡进行分析研究。该算例已被很多研究者应用分析，因此其结果能够较好的反映强度折减法的效果。土坡几何尺寸见图1，边坡有限元模型如图2所示，土体参数如表1所示。

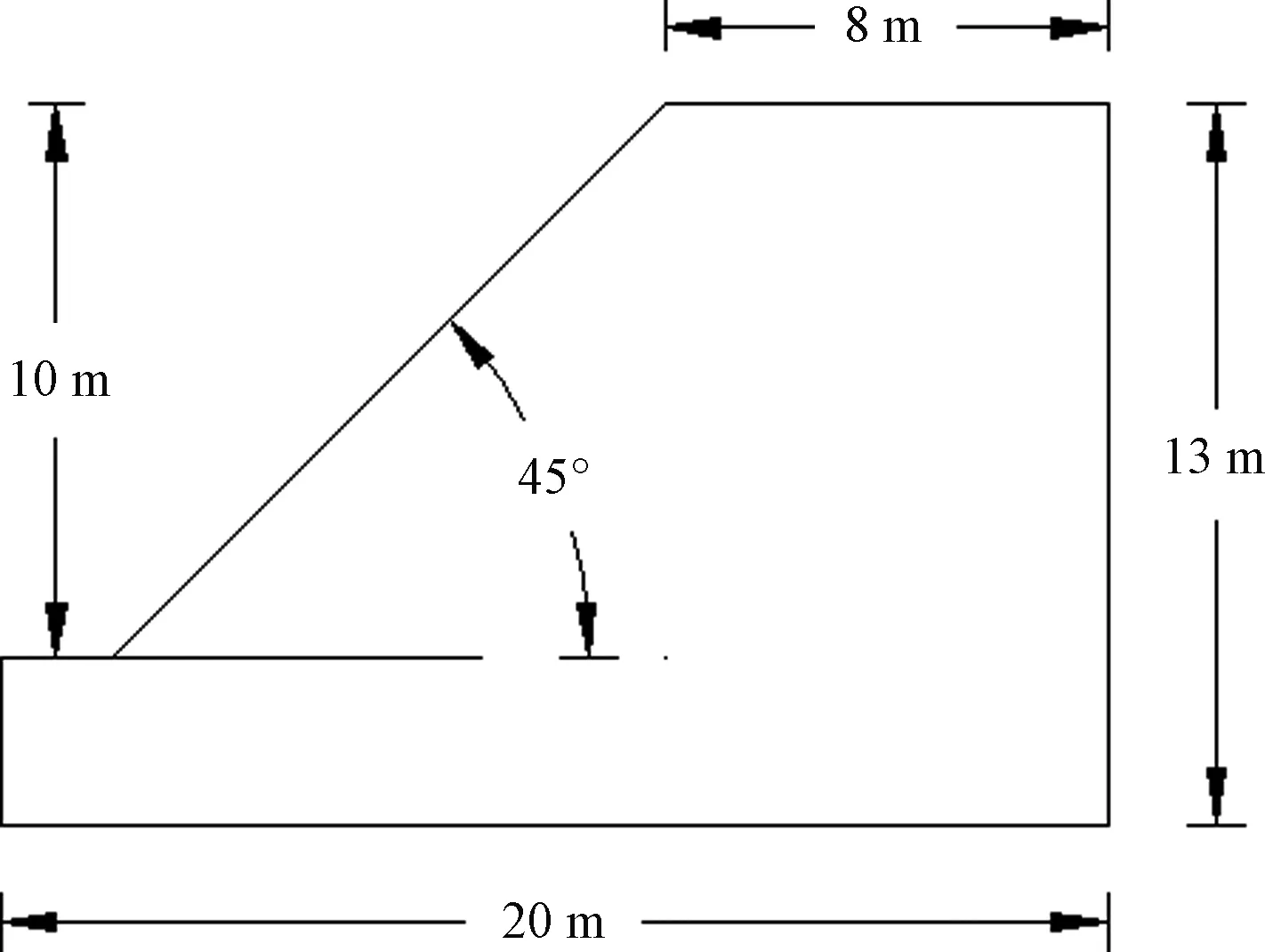
图1 边坡几何模型[11]Fig.1 Geometric model of slope[11]

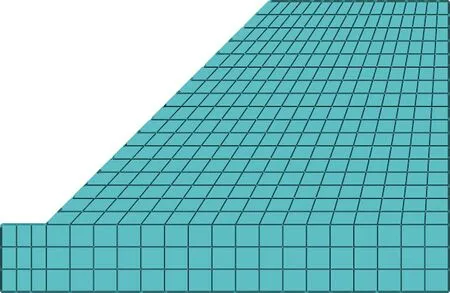
图2 边坡有限元模型[11]Fig.2 Finite element model of slope[11]

表1 土体基本力学参数表[11]

2.2 参数选取

在有限元中，对于边坡稳定性系数的影响主要建模与材料参数的赋予过程。而在强度折减法中，主要是对材料的参数进行折减，本文中主要采取Mohr-coulomb模型，主要参数有φ、c、E、μ以及Ф，因此取这5个参数作为本文分析的敏感性因素。

其中，c、φ的变化值分别取(12，14，16，18，20)和(20，22，24，26，28)。由张培文等[12]可知，弹性模量E不能取得太小，一般在100 MPa以上，所以弹性模量E取(100，200，300，400，500)；泊松比μ需要满足式1-2μ≤sinφ，即μ≥0.329，所以泊松比取(0.33，0.35，0.37，0.39，0.41)。唐晓松等[13]为分析土体剪胀的影响情况，采用非关联流动法则，认为剪胀角的变化范围为(0,φ)，所以本文剪胀角Φ取(0，5，10，15，20)。

3 边坡稳定性敏感性灰色关联分析

3.1 关联度计算

将上文分析影响因素取值作为子序列。令某一影响因素进行变化，其他影响因素不变，利用有限元强度折减法求出的边坡稳定性系数作为母序列矩阵。边坡稳定性系数的求取采用计算不收敛判据[14]。子序列和母序列如下：

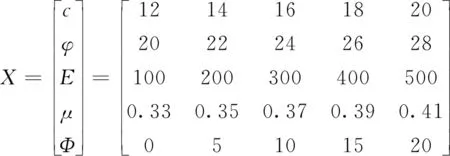
将X、Y矩阵通过(3)、(4)式进行处理，从而得到差异序列矩阵Δ：

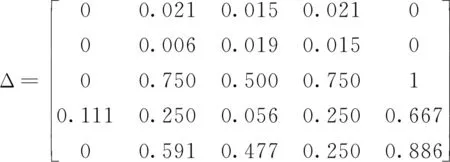
由式(5)～(7)可求得关联系数矩阵L为：

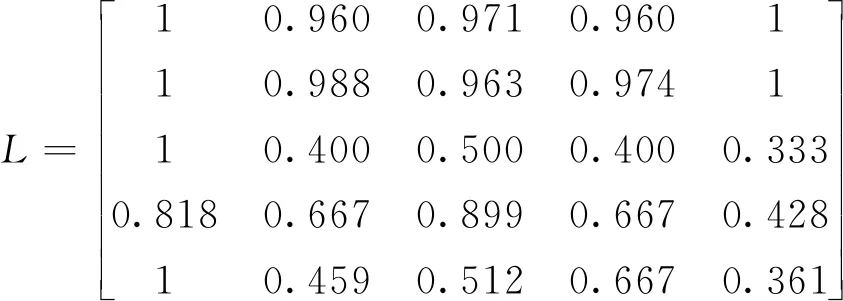
最后，由式(8)求得关联度矩阵G为：

3.2 敏感性评价

目前，许多学者基于有限元软件，研究了边坡稳定性影响要素敏感性分析。张培文等[12]通过对弹性模量和泊松比的折减算例得出泊松比μ对于边坡稳定性有一定的影响，而弹性模量无明显影响。何培勇等[15]将有限元的应力应变计算与强度折减法理论相结合，得出剪胀角对边坡稳定性的影响，但他们都未深入研究几个参数之间的影响程度大小。

由上文求解得到的灰色关联度矩阵分析可知，对于有限元强度折减法求解的边坡稳定性系数，其影响因素的敏感性按从大到小排列依次是：φ、c、μ、Ф、E，即对边坡稳定性的影响大小。其中，边坡稳定性系数对c、φ值的改变最为敏感，其关联度达到了0.97以上，其次是μ和Ф对稳定性系数的影响。由母序列矩阵Y可看出，弹性模量E对边坡稳定性系数几乎没有影响。这与上述两位学者的研究结果如出一辙。因此，利用强度折减法计算边坡稳定性系数时应主要考虑黏聚力c、内摩擦角φ的影响。由于φ的影响程度比c的影响程度更大，在双强度折减法中c的折减系数应大于φ的折减系数。另外，由于μ和Ф对边坡稳定性有一定影响，因此可对泊松比和剪胀角进行一定的折减。

4 边坡稳定性有限元模拟结果分析

若c、φ值减小，边坡的破坏面将发生改变，下滑力与抗滑力也将改变。图3为基本算例(采用表1参数)边坡破坏时的位移分布图。从ABAQUS有限元模拟的结果分析，c、φ值越小，边坡发生塑性应变区域就越大，滑动面也相应的发生改变。如图4所示，当φ=28°时，边坡滑动面比基本算例更加迫近临空面，最终与极限平衡原理求解边坡的稳定性系数有一定差异，所以需要同时对其他参数进行调整，使边坡的滑动面变化较小。

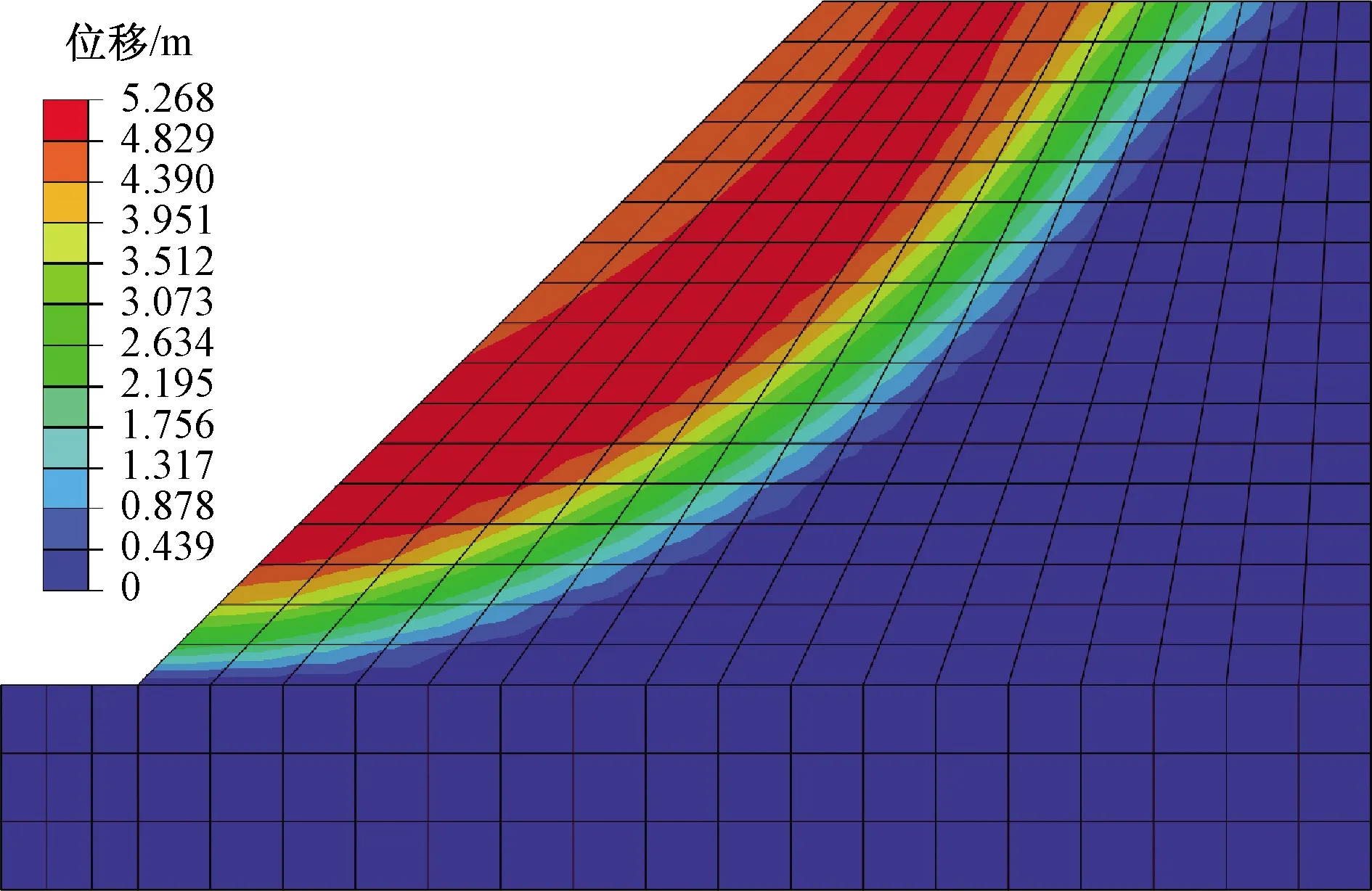
图3 基本算例位移分布图Fig.3 Displacement distribution of basic example

图4 φ=28°时边坡位移分布图Fig.4 Slope displacement distribution while φ=28°

4.1 弹性模量影响分析

从图5、图6可以看出，E的变化仅改变边坡位移的大小，对于滑动面几乎没有影响。再结合灰色关联分析中的母序列矩阵，可知E对边坡稳定性系数几乎没有影响。因此可不考虑E在强度折减法中的影响。

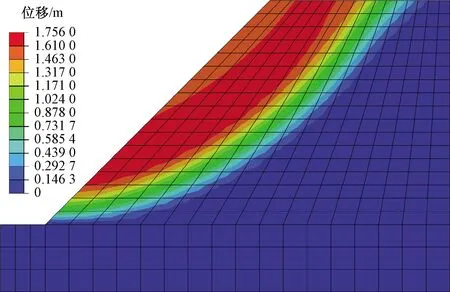
图5 E=300 MPa时边坡位移分布图Fig.5 Slope displacement distribution while E=300 MPa

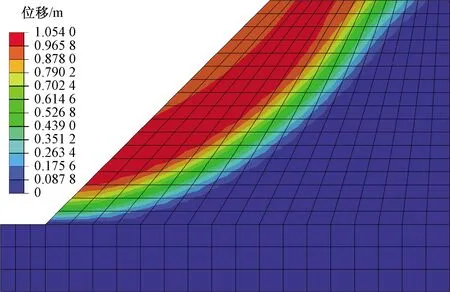
图6 E=500 MPa时边坡位移分布图Fig.6 Slopedisplacement distribution while E=500 MPa

4.2 泊松比影响分析

从图7、图8可看出，随着泊松比μ的增大，边坡的位移逐渐减小，μ的变化并未改变边坡滑动面的大小。再由母序列矩阵中μ相应行可看出，μ对边坡稳定性系数的求解有一定的影响。因此，须考虑在强度折减法中对μ进行折减。

图7 μ=0.33时边坡位移分布图Fig.7 Slope displacement distribution while μ=0.33

图8 μ=0.41时边坡位移分布图Fig.8 Slope displacement distribution while μ=0.41

4.1和4.2的结论与张培文等[12]的研究结果一致，也说明了分析的可靠性。

4.3 剪胀角影响分析

从图9、图10可看出，Ф增大，边坡滑动面更加逼近临空面。另外，边坡的位移大小与Φ并非线性关系。当Ф=20°时，边坡在滑动过程中发生了无限制的体积膨胀现象，证明了唐晓松等[13]研究的正确性。从母序列矩阵中可看出，边坡稳定性系数随Ф的增大呈先增大后减小的趋势，说明Ф对边坡稳定性系数有一定的影响。因此须在强度折减法中考虑Ф的影响。

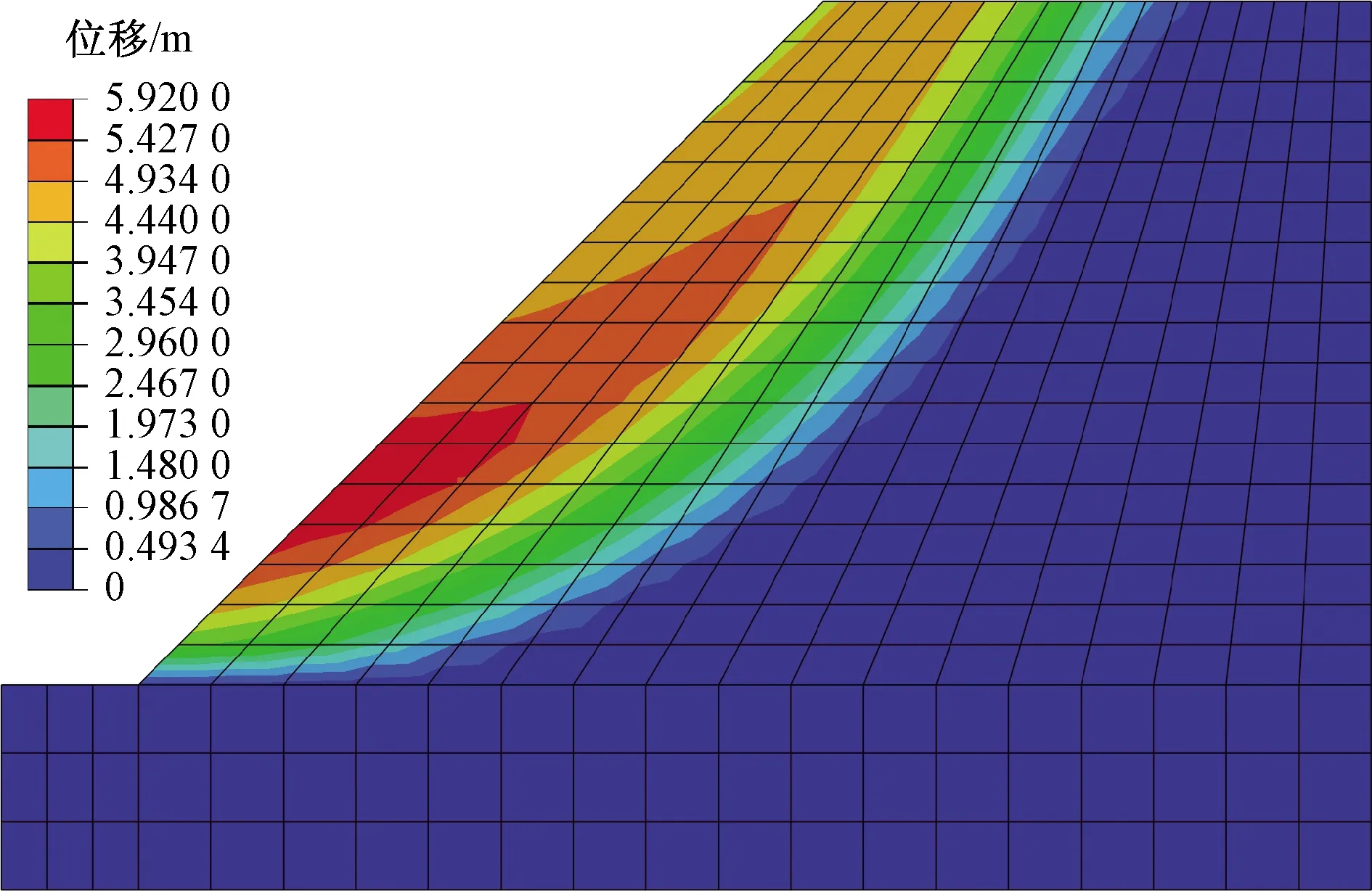
图9 Ф=10°时边坡位移分布图Fig.9 Slope displacement distribution while Ф=10°

图10 Ф=20°时边坡位移分布图Fig.10 Slope displacement distribution while Ф=20°

5 结论

(1)将灰色关联法运用于强度折减法中，分析了φ、c、μ、Ф、E对边坡稳定性的影响程度，建立其内在联系，克服了双强度折减法中假设两折减系数比例以及不考虑μ、Ф、E折减的盲目性。

(2)影响因素的敏感性按从大到小排列依次是：φ、c、μ、Ф、E。其中，边坡稳定性系数对c、φ值的改变非常敏感，其关联度达到了0.97以上，且φ的关联度比c更大，说明φ对边坡稳定性的影响更大，在双强度折减法中黏聚力折减系数应比内摩擦角折减系数更大。其次是μ和Ф的影响，说明其对边坡稳定性有一定影响，在双强度折减法中也应考虑对这两者的折减。E对稳定性系数的求解几乎没有影响。

(3)通过对有限元位移分布图的分析，E、μ对滑动面几乎没有影响，但泊松比对边坡稳定性系数有一定影响；Ф的增大将破坏面逼近临空面，且对边坡稳定性系数有一定影响。因此，应考虑在强度折减法中μ和Ф的折减。