基于振动台试验的地震作用下岩质边坡位移演化特征

2020-06-30毕鹏程车爱兰袁刚烈

中国地质灾害与防治学报 2020年3期

毕鹏程，车爱兰，袁刚烈

(上海交通大学船舶海洋与建筑工程学院，上海 200240)

0 引言

2008年的汶川地震引发了多处边坡崩塌、失稳滑坡等地质灾害，其中在龙门山地区的滑坡中近60%出现在具有层状结构的岩质边坡中[1]。汶川地震后，灾区周边地区地质结构也受到扰动，使得地震引起的地质灾害更加频繁且严重。近年来，西部地区发生了多次大地震，例如2013年甘肃省定西地震诱发了约600余处地质灾害[2]，2014年云南省普洱市景谷县地震引发边坡崩塌滑坡，这些地震灾害引发的工程问题造成了重大的经济损失[3]。云南省内在2016年开始实施46个高速公路重点项目，蒙文砚、宣曲、新嵩昆、昆明东南绕城、香丽、华丽等高速公路项目正在推动中，这些工程都涉及到地震作用下岩质边坡性能演化与安全控制问题[4]。

边坡动力稳定性影响因素具有不确定性，动力抗滑稳定安全度判据具有多元性[5]。由于边坡滑动时滑裂面以上的岩体同时滑动，因此桥基边坡稳定平衡系统是由桥基、随桥基而动的基岩、软弱结构面、软弱结构面下部的基岩构成的[6]。所以，桥基边坡抗滑稳定安全度的判据具有多元性特征，不能用单一的安全系数来衡量，而应该用桥基、基础的应力、位移等综合指标进行判定。在实际工程中，位移监测可为分析滑坡的结构和成因、评价边坡的稳定性及发展趋势等提供重要信息。将位移监测与边坡破坏现象结合起来，能准确地判断边坡的破坏阶段，评价和预测边坡施工及其使用过程中边坡的稳定状况[7]。

振动台模型试验是研究边坡强震动力响应和破坏过程极为有效的方法之一[8-9]。LIN M L等[10]利用大型振动台试验对边坡在地震下的动力响应进行研究，认为边坡破坏局限在坡体表面，破坏深度较浅。黄润秋等[11]采用大型振动台试验研究了地震作用下顺层岩质边坡动力响应和破坏模式，发现边坡的整体破坏机制为地震使坡面中部出现裂缝，裂缝贯通从而发生高位滑坡，最终转化为碎屑流堆积坡脚。以上学者在振动台试验中，主要通过加速度传感器研究边坡的动力响应规律，进而分析其破坏规律。目前针对复杂地质结构边坡的位移规律方面的研究相对欠缺，利用位移响应特性对其稳定性进行判定能更深入地研究其破坏机理。在位移响应方面，ABDOUN等[12]利用阵列式位移计测试了桥台边坡的位移，并将此技术应用于日本国立防灾技术研究所的振动台试验上，取得了良好的位移数据。但利用传感器测试位移的缺点在于测点少，精度有限。刘君等[13]将PIV技术应用于振动台模型试验中，利用相机对边坡侧面的位移进行了观测并描绘出其滑动面，然而此方法只能观测测点的平面位移特性，无法反映测点的空间位置信息。本文中采用的XTDIC光学测量系统能观测测点在三维空间中的位移，且测距5 m内测量误差为0.05～0.1 mm，可观测边坡表面大量测点的位移变化。

本文以华丽高速公路金沙江特大桥桥址边坡为研究对象，通过大型振动台模型试验，研究不同地震烈度输入下(包括不同峰值加速度大小以及不同输入方向)岩质边坡的位移响应特性，分析位移响应特性与边坡失稳破坏的关系。通过模型中的结构面的设置，明确地震作用下不良地质构造对边坡表面位移及稳定性的影响。

1 振动台试验

本次振动台模型试验采用中国地震局兰州地震研究所的大型电伺服式振动台，由日本国际计测器株式会社生产。该振动台台面尺寸为4 m×6 m，总共由28台伺服电机驱动，可实现水平方向和垂直方向地震荷载的模拟，转子惯性扭矩为7.0×10-3kg·m2，水平、垂向最大加震力均可达600 kN。

1.1 工程背景

金沙江大桥位于金沙江中游河道，该段金沙江总体呈近SN向发育，河谷呈“V”型，为纵向单斜谷，两岸地形基本对称，山体雄厚，地形陡峻。因受地层产状和顺河向陡倾角结构面影响，两岸岸坡多形成阶梯状地形，桥位区地势较高，整体坡度较大，地下水埋藏深，地表水及地下水不发育，对桥梁工程整体影响较小。华坪岸为顺向坡，总体坡度20°～30°，地形地貌如图1所示。其工程地质岩组主要包括玄武岩(微新)、T2结构面、后缘陡倾结构面。华坪岸剖面如图2所示，其中T2结构面主要由凝灰岩组成，后缘陡倾结构面为绿帘石、石英错动带，为硬性结构面，面有擦痕。根据《中国地震区划图》，华坪岸边坡位于中甸-大理地震带，该地区抗震设防烈度为Ⅷ度。

图1 华坪岸地形地貌Fig.1 Topography and geomorphology of the Huaping Slope

图2 华坪岸剖面图Fig.2 The profile of Huaping Slope

影响边坡稳定性的主要因素有地形地貌条件、岩石性质、岩体结构面以及外力荷载等因素。根据华丽金沙江大桥桥址边坡的地形地貌等工程地质条件，目前金沙江两岸边坡在天然条件下是相对稳定的，而在地震荷载作用下的稳定性还有待进一步的研究。因此，地震附加荷载和结构面的组合是该桥址边坡稳定性的主要控制因素。本次振动台试验针对金沙江大桥华坪岸桥址边坡地质条件，研究其在地震荷载下的稳定性。

1.2 模型设计与制作

试验采用刚性密封模型箱，模型箱内箱尺寸为2.8 m× 1.4 m× 1.4 m。将山体边坡简化为平面应变问题，取其一个截面进行分析，考虑的实际边坡范围内坡高约450 m，坡长约900 m，坡脚为30°。根据试验条件，采用相似准则最终确定模型几何尺寸相似关系Cl为375∶1，因此设计的边坡模型高1.3 m，宽1.4 m，长2.5 m(图3)。按照模型几何尺寸相似关系，模型材料的物理力学参数的相似计算如表1所示。

图3 边坡模型设计图Fig.3 Slope model design

表1 相似常数

通过室内试验得到了玄武岩的物理力学参数，凝灰岩及陡倾结构面岩石力学参数根据规范取其工程经验值(表2)。

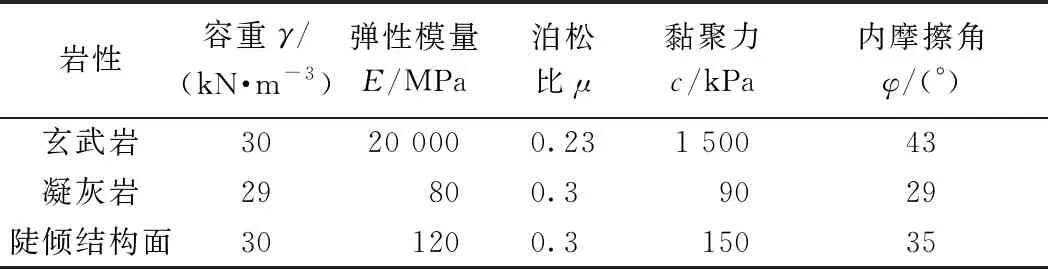
表2 原型边坡岩石物理力学参数

经相似准则计算出玄武岩及凝灰岩的物理力学参数后，通过不同配合比、不同材料试样的密度试验及静三轴试验，最终确定采用的模拟材料及配比为：水泥∶砂∶铁粉∶黏土∶混合剂(速凝剂和减水剂)∶水=0.325∶17∶9∶0.4∶0.03∶5.0。T2凝灰岩夹层缩尺后平均厚度约0.5 cm，采用雪弗板(PVC)模拟T2结构面。模拟材料的物理力学参数如表3所示。考虑到陡倾结构面的几何特性以及模型砌筑方式，试验中将陡倾结构面考虑为模型砌筑时的砌缝，并在砌缝中填入松砂，模拟陡倾结构面的内摩擦角φ=35°。

表3 模拟材料的物理力学参数

由于模型的体积大会引起制作不便、养护困难等问题，且在浇筑的过程中因浇筑时间的不同会出现材料特性差异。采用砌块堆积的方式制作边坡模型，堆砌完成后，将坡面多余部分削去。并在上部砌块之间的砌缝中填充相同材料，尽量使其形成一个整体。

实际制作过程中，先将材料搅拌均匀后浇筑制作模型砌块，在干燥通风良好的室内放置三天后达到预设强度，最后进行边坡模型的砌筑操作。模型中的T2结构面采用PVC板放入设定的模块的设定方向及位置。制作完成的边坡模型如图4所示。定义x轴为沿坡长方向，y轴为沿坡宽方向，z轴为竖直方向。

图4 边坡模型Fig.4 Model slope

1.3 位移观测

位移测试采用光学测量技术，利用苏州西博三维科技有限公司研发的XTDIC测量系统采集位移数据(图5)。动态位移测量系统基于双目立体视觉技术，采用两个高速摄像机实时采集被测物体各个位移阶段的图像，利用准确识别的标志点或者数字散斑(包括编码标志点和非编码标志点)实现立体匹配，重建出物体表面点的三维空间坐标和位移，计算得到物体的位移量。

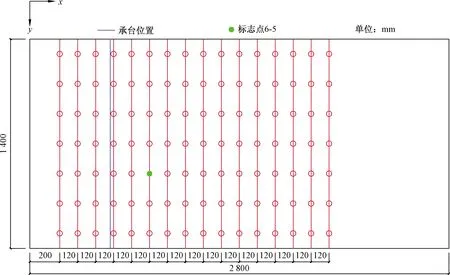
图6 坡面位移标志点的布设Fig.6 Layout of displacement mark

测量采用两台两百万像素摄像机，支持低速到高速采集，最高采集频率340 Hz，测距5 m内测量误差约为0.05～0.1 mm。本次试验采集频率为50 Hz，即采样间隔为0.02 s。

测量摄像头标定好以后固定不动，在开始震动后连续性采集，通过计算出各个标志点每个状态的空间坐标从而得到标志点的位移波形。位移观测选取边坡坡面，标志点采用14 mm非编码，标志点的布设如图6所示，在x方向上共设置16排标志点，每排7个。同时在模型箱上固定一标志点作为基准，最终将边坡上标志点的位移波形减去基准点波形后得到边坡标志点的相对位移波形，因此后文所提及的均为边坡相对于模型箱的位移波形。

1.4 试验荷载工况

该振动台满载时水平加载最大加速度为1.7g，垂直方向为1.2g，响应频率为300 Hz，满足实验设计要求。垂直与水平荷载分别采用2008年汶川地震甘肃文县基岩台记录的汶川地震记录波垂直向波形与东西向波形，其卓越频率为7.6 Hz，东西向波形及频谱特性如图7所示。汶川地震波持续时间长达160 s，其中强震持时超过20 s。

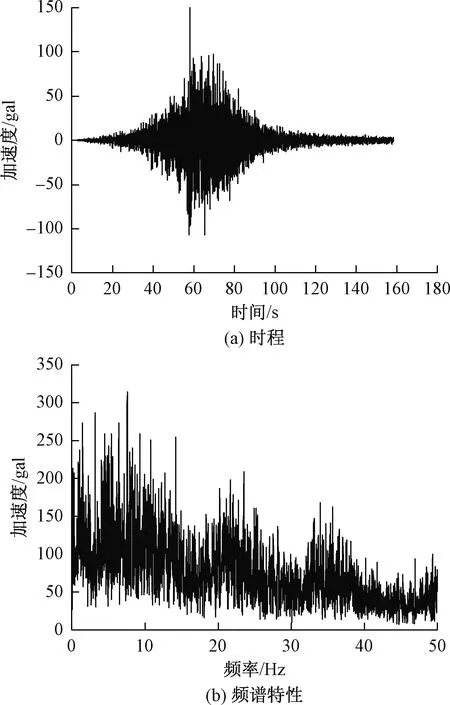
图7 汶川地震记录波(东西向)Fig.7 Seismic wave recorded during Wenchuan earthquake

为了研究试验模型在不同烈度的地震力作用下的动力响应，按照Ⅵ度、Ⅷ度、Ⅸ度烈度递增的顺序分水平方向(x方向)和垂直方向(z方向)对模型进行加载，共加载了6个工况(表4)。

在地震力较小时，边坡处于弹性变形阶段；随着地震力的增大，边坡进入塑性变形阶段，变形不可逆。在位移数据采集时对标识点及光学测量设备进行重置，保证位移波形采集的是每次震动引起的位移波形。对于模型本身无法进行可逆重置，因此模型的总变形是累计变形。

表4 试验加载工况

2 边坡模型的位移响应特性

2.1 位移波形

图8为水平方向(x方向)加载时，边坡表面标志点6-5(其位置见图6)在Ⅵ度及Ⅸ度地震烈度工况下的x方向和z方向的位移波形图。可以看出水平输入时z轴方向的位移响应很小，Ⅵ度时仅在0.3 mm以下，Ⅸ度时存在约3 mm的永久位移，而x轴方向位移响应较大，Ⅵ度时最大响应达到了3 mm，在Ⅸ度时，最大响应达到了32 mm，永久位移达到了约13 mm。可以认为，采用光学测量的手段，可以很好的观测边坡模型表面的动态位移。在水平输入(x方向)时，x方向位移占主导地位，并且垂直输入(z方向)工况也表现出同样的规律。

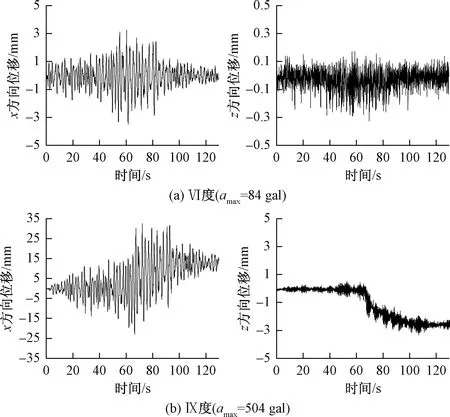
图8 典型测点位移波形(水平输入)Fig.8 Displacement wave at measuring point

2.2 位移响应特性

根据各测点的位移波形，取其振幅绝对值的最大值，获取该测点的最大位移(PGD，Peak Ground Displacement)。提取表面所有测点最大位移，将其按对应位置分布在坡面上可得到各工况的坡面最大位移分布图。水平加载工况只考虑x方向PGD，垂直加载工况只考虑z方向PGD。

图9、图10分别为汶川地震波输入时Ⅵ度、Ⅷ度及Ⅸ度烈度下垂直加载时z向PGD分布图和水平加载时x向PGD分布图。可以发现，在地震烈度较小(Ⅵ度左右)时，边坡整体位移较小且无明显相对位移。随着地震烈度的增大，达到约Ⅷ度(336 gal)时，在边坡的陡倾结构面处(承台位置)出现明显的相对位移。地震烈度达到Ⅸ度(504 gal)时，在陡倾结构面处的相对位移更加明显。陡倾结构面处至坡脚附近PGD基本不变，可以认为该部分发生整体位移。

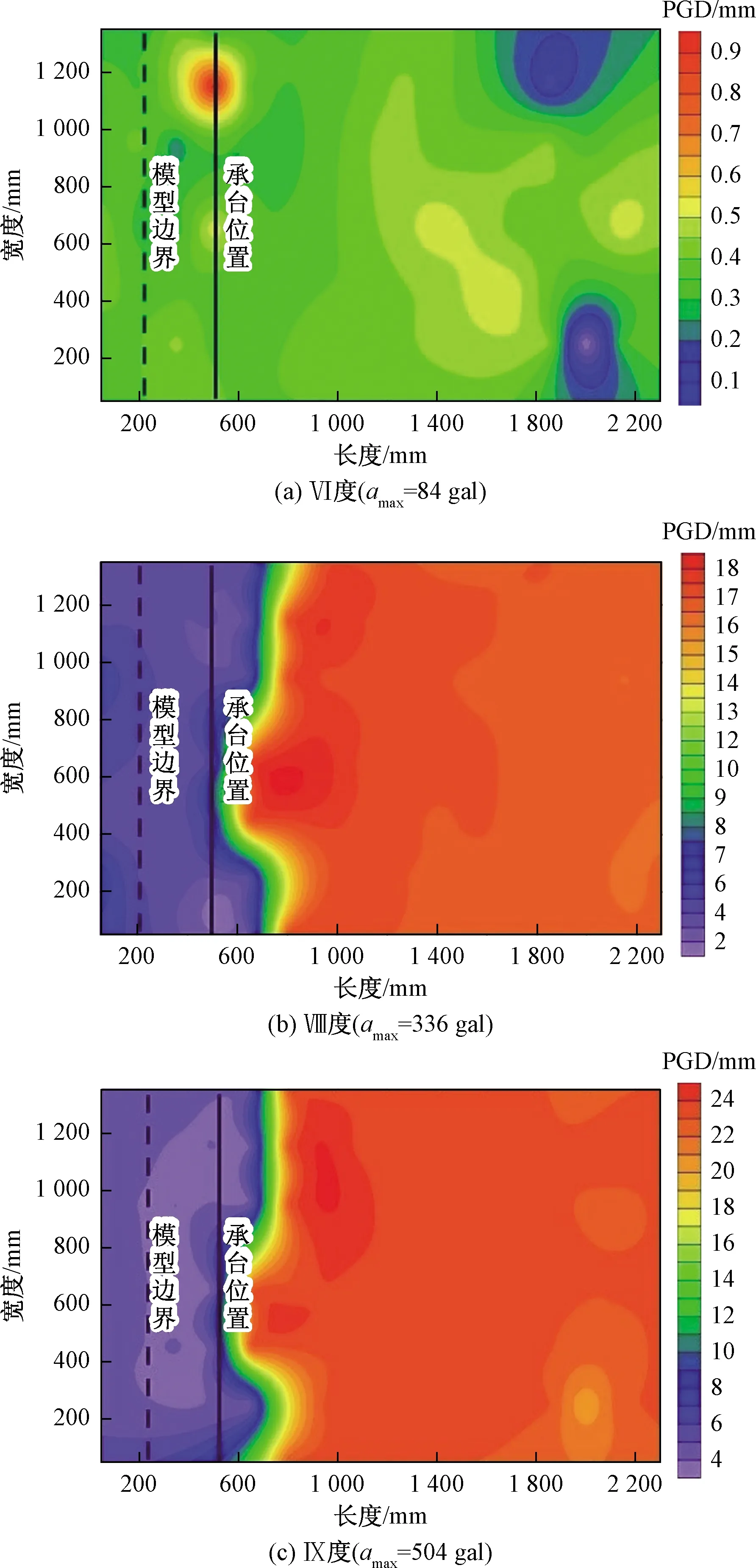
图9 垂直加载时z向PGD分布Fig.9 Distribution of PGD in z direction (vertical loading)

图10 水平加载时x向PGD分布Fig.10 Distribution of PGD in x direction (horizontal loading)

标志点在x方向上共16排，每排有7个点，取每排标志点PGD的平均值，可得到各工况下每排观测点的平均PGD的分布图(包括x向与z向)(图11)。在垂直与水平方向输入的工况中，分别将各排标志点的x向与z向PGD整合为矢量并反映在模型侧面，可得到侧视坡面PGD分布图，为便于观察比较，绘图时将实际的PGD扩大了10倍(图12)。

可以发现，地震波垂直输入的工况中，z向PGD远大于x向PGD，占主导地位；水平输入的工况中，x向PGD远大于z向PGD，占主导地位。无论是水平输入还是垂直输入，Ⅵ度(84 gal)地震烈度输入时，所有标志点PGD均在5 mm以下，且无明显相对变化。Ⅷ度(336 gal)时，在承台附近位移响应呈现明显突变，其两端出现明显的相对位移，最大达到约1.4 cm。Ⅸ度(504 gal)时，两端出现的相对位移进一步增大，最大达到约3 cm。

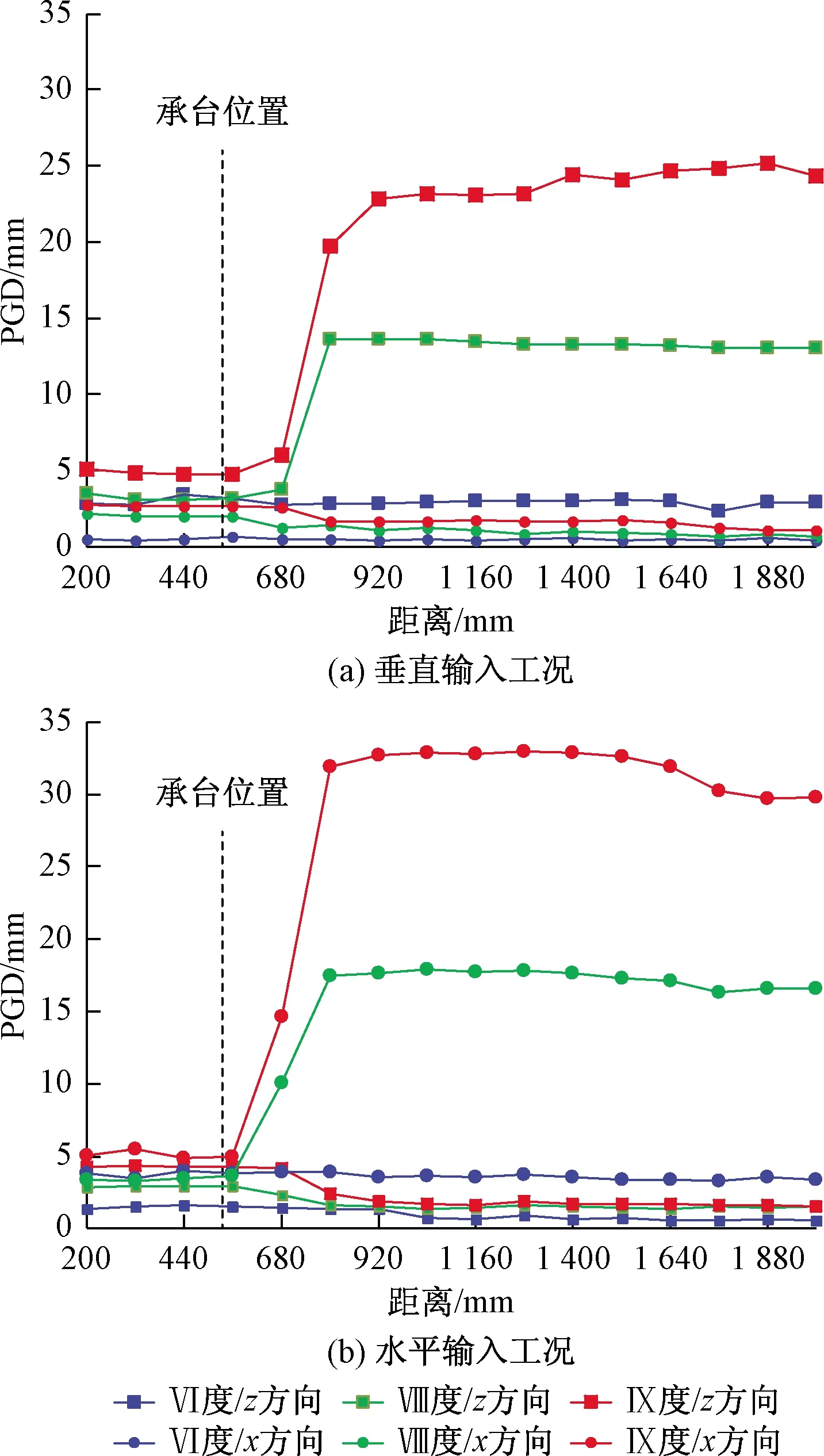
图11 沿坡向平均PGD分布Fig.11 Average PGD along the slope

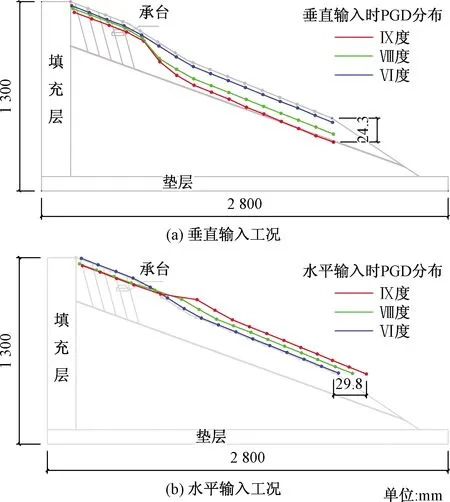
图12 坡面PGD分布(侧视图)Fig.12 PGD distribution on the slope surface (side view)

2.3 位移演化规律

通过位移响应分布可以认为坡体呈现整体滑动破坏，因此将整体滑动部位内所有测点的PGD及永久位移取平均值，根据地震波输入方向分别分析其在Ⅵ度(84 gal)、Ⅷ度(336 gal)、Ⅸ度(504 gal)时的变化规律(图13)。

PGD及永久位移演化规律基本相同，随着输入地震波峰值加速度的增大，整体滑动部分的PGD与永久位移不断增大。无论是水平输入还是垂直输入，Ⅷ度(336 gal)之前，PGD与永久位移呈线性增长，Ⅷ度(336 gal)之后呈现加速增长趋势，说明边坡在这一阶段进入非线性状态，边坡处于不稳定状态。到达Ⅸ度(504 gal)时，边坡最终失稳破坏。Ⅸ度(504 gal)时水平输入下PGD达到32.46 mm，垂直输入下PGD达到24.89 mm。可以认为，边坡在受到地震力累计作用下进入不稳定状态，在如降雨、地震等其他诱发条件下，发生滑动破坏。位移演化规律可用于灾后边坡位移监测、预警等。

图13 整体滑动区域PGD及永久位移Fig.13 PGD and permanent displacement at overall sliding area

3 边坡失稳破坏特征

每个工况加载后，对边坡模型表面的裂缝扩张情况进行描绘，各阶段的描绘状态如图14所示。随着地震力的施加，首先在坡底剪出口处出现少许裂缝；地震烈度达到Ⅷ时，承台位置附近开始出现裂缝并不断扩张；当地震烈度达到Ⅸ时，承台附近及剪出口处的裂缝不断扩张并贯通，最终边坡模型失稳破坏。此外，随着烈度的增大，砌砖之间产生裂隙并逐渐扩张，最大可达2～4 mm，该情况可能与模型砌筑过程中砌砖、砌缝成型时间差异导致的力学性能不一致有关，但对该模型的破坏模式基本无影响。

图14 模型坡面裂缝开展情况Fig.14 Description of cracks during test

图15展示了边坡破坏过程，分别为Ⅵ度、Ⅷ度及Ⅸ度水平输入工况下边坡的表面状态，由于水平与垂直工况下位移演化规律基本一致，而水平输入工况位移更为明显，因此选取了水平输入工况的现场照片。图16、图17揭示了模型失稳后破坏情况，从俯视图中可以发现坡底出现明显的剪出口，剪出口处产生大量的裂缝并随之扩张，在坡顶陡倾结构面附近产生大量的倾角方向裂缝，且该区域右侧位置砌块破碎严重，可见该区域岩体强度基本丧失，危及承台所在桥址；从侧视图中可以发现坡体内部距离坡表50～200 mm处存在大量扩张裂缝，判断其为滑坡滑动面，并随着水平输入烈度的增加，滑动面逐渐贯通。综上，陡倾结构面处(承台位置)为控制性滑动面的后缘面，剪出口位于坡脚附近，陡倾结构面处至坡脚附近间坡体呈整体滑动趋势。